7090996907

W. Guzicki: Zadania z kombinatoryki 11

17.    W klasie liczącej 30 uczniów wielu uczniów gra w brydża, szachy lub warcaby. W brydża gra

16    uczniów, w szachy gra 13 uczniów, w warcaby gra 10 uczniów. Jednocześnie w brydża i szachy gra 7 uczniów, w brydża i warcaby gra 5 uczniów, w szachy i warcaby gra 4 uczniów. Wreszcie 3 uczniów gra we wszystkie trzy gry. Ilu uczniów nie gra w żadną z tych trzech gier?

Rozwiązanie. Tym razem zastosujemy zasadę włączeń i wyłączeń dla trzech zbiorów. Przy naturalnych oznaczeniach zbiorów mamy:

\B u s u w\ = \B\ + |S| + \w\ - \b n s\ - \B n w\ -15 n w\ + \B n s n w\ =

= 16 + 13 + 10 - 7 - 5 - 4 + 3 = 39 - 16 + 3 = 26.

Stąd wynika, że 4 uczniów nie gra w żadną z tych trzech gier.

18.    W klasie liczącej 30 uczniów wielu uczniów gra w brydża, szachy lub warcaby. W brydża gra

17    uczniów, w szachy gra 13 uczniów, w warcaby gra 11 uczniów. Jednocześnie w brydża i szachy gra 6 uczniów, w brydża i warcaby gra 7 uczniów, w szachy i warcaby gra 5 uczniów. Wreszcie 3 uczniów nie gra w żadną z tych trzech gier. Ilu uczniów gra we wszystkie trzy gry?

Rozwiązanie. Jeszcze raz zastosujemy zasadę włączeń i wyłączeń dla trzech zbiorów. Przy naturalnych oznaczeniach zbiorów mamy:

\BUSU w\ = |B| + |Sj + \w\ - |Rn5| - |fln w\ - |Sn w\ + |snsn w\ =

= 17 + 13 + 11 - 6 - 7 - 5 + \B n S n W\ = 41 - 18 + \B D S n W\ =

= 23 + |B n s n w\.

Ponieważ 3 uczniów nie gra w żadną z tych trzech gier, więc \B U S U W\ =27. Stąd dostajemy

\b n s n w\ = \b u s u w\ — 23 = 27 — 23 = 4,

a więc we wszystkie trzy gry gra czterech uczniów.

Zadania 15, 16,17 i 18 możemy łatwo rozwiązać graficznie, wykorzystując tzw. diagramy Venna. Najpierw popatrzmy na rozwiązanie zadania 15.

Rysujemy dwa okręgi przedstawiające zbiory B i S. Musimy zadbać o to, by te okręgi się przecinały. Dzielą one wtedy płaszczyznę na 4 obszary; nazywamy je składowymi. Na poniższym rysunku są one ponumerowane liczbami rzymskimi I, II, III i IV:

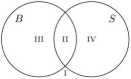
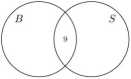
Obszar o numerze I, leżący na zewnątrz obu okręgów, oznacza te elementy, które nie należą do żadnego ze zbiorów B i 5, a więc tych uczniów, którzy nie grają w żadną grę (w zadaniu 15 mamy właśnie dowiedzieć się, ile ta część ma elementów). Obszar o numerze II, leżący wewnątrz obu okręgów, oznacza te elementy, które należą do obu zbiorów jednocześnie, a więc tych uczniów, którzy grają w obie gry razem (w zadaniu 15 mamy w tej części 9 elementów). Zatem w rozwiązaniu zadania 15 w ten obszar wpisujemy liczbę 9:

Warszawa, 19-20 października 2013 r.