1933501737

8 PODZIAŁ MACIERZY NA PODMACIERZE

9

Jeżeli wszystkie elementy macierzy leżące pod jej główną przekątną są równe zero

aij = 0 dla i > j    (36)

to macierz taką nazywamy macierzą górnotrójkątną Przykład macierzy górnotrójkątnej A o wymiarze 5x5:

	' 1	2	3	3	5
	0	3	7	1	3
A =	0	0	3	2	5
5x5	0	0	0	4	4
	0	0	0	0	2

Jeżeli A jest macierzą dolnotrójkątną to łatwo jest znaleźć rozwiązanie równania macierzowego

Ax = c    (38)

które wynosi:

ci

xi = — an

Xi = —(Ci

Y, aijXj) dla i = 2,2,3..., n

3= 1

(39)

W podobny sposób można rozwiązać równaie macierzowe z macierzą A górnotrójkątną (rozwiązując tym razem ykład od ostatniego równania).

8 Podział macierzy na podmacierze

Macierz może zostać podzielona na mniejsze macierze nazywane podmacie-rzami. Przykład:

an	a\2	ai3
022	a22	<*23 .
«31	<*32	«33

gdzie podmacierze mają postać:

An —	an	«12
	«22	022
A21 =	«31	<232

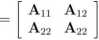
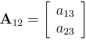
A22 — <*33

(40)