3262347663

A zatem istnieje możliwość określenia gęstości ładunku przestrzennego poprzez procedurę dekonwolucji, jeśli AT jest znane. Jednakże ze względu na niedokładność procedury dekonwolucji nie jest możliwe otrzymanie jednoznacznego rozwiązania dla q_x(x) lub Pi(x). W idealnych warunkach możliwe jest uzyskanie tylko 5 do 10 przestrzennych współczynników Fouriera dla rozkładu ładunku przestrzennego. Biorąc pod uwagę błędy pomiarowe odpowiedzi napięciowej, dokładnie można wyznaczyć tylko kilka współczynników Fouriera. Z dyskusji w [54] wynika, iż dla dokładności pomiaru AVrzędu 0,1 % tylko od 3 do 9 współczynników (rzeczywista ilość współczynników zależy od lokalizacji chmury ładunku w dielektryku) może być znaleziona. Podobne problemy występują podczas pomiarów rozkładu polaryzacji w dielektrykach polarnych. Wtedy należy uwzględnić wzór dotyczący ładunku polaryzacyjnego. Dwa wzory opisujące ładunek przestrzenny i polaryzację sugerują, że istnieje możliwość określenia albo rozkładu przestrzennego ładunku albo polaryzacji.

Dokładniejsze rozważania pokazują, że równanie (3.4) można rozważyć osobno w przypadku istnienia ładunku i/lub polaryzacji. Biorąc pod uwagę ładunek przestrzenny napięcie biegu jałowego wyraża się zależnością [55]:

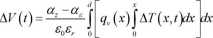
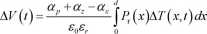
(3.5)

natomiast dla polaryzacji (3.6)

Rozważania pokazują jedynie przypadki, w którym jednoznacznie wiadomo, że w badanym materiale jest rzeczywiście rozkład ładunku przestrzennego lub polaryzacja.

Rozdzielczość jest największą z wad metody TPM. Można pokusić się

0    stwierdzenie, iż rozdzielczość metod termicznych pozostawia wiele do życzenia, dodatkowo zależy od głębokości analizowanego obszaru próbki [66], W metodzie TPM występują takie same problemy, najwyższą rozdzielczość można uzyskać jedynie w obszarze przyelektrodowym. W tym obszarze rozdzielczość metody jest określona ale

1    ograniczona czasem trwania impulsu termicznego t_p. Amjadi z współpracownikiem uzyskał maksymalną rozdzielczość na poziomie 11 nm stosując laser Nd:YAG o czasie trwania impulsu 70 ps [56],

18