3545336449

Zadanie 7.3. Jak wygląda macierz przyległości prostego grafu dwudzielnego? Zaproponuj mniejszą macierz określającą przyleglość w takim grafie.

Zadanie 7.4. Znajdź liczbę spacerów długości k między

i)    dwoma różnymi wierzchołkami grafu K,i;

ii)    dwoma różnymi nieprzyległymi wierzchołkami w #3,3;

iii)    dwoma przyległymi wierzchołkami #3,3.

Uwzględnij następujące wartości k:

a. 2 b. 3 c. 4 d. 5.

Zadanie 7.5. Prawdziwe jest następujące twierdzenie:

Niech A będzie macierzą przyległości grafu prostego G o zbiorze wierzchołków [n] oraz niech A^k = Bk = {&y}jje[n]-Wtedy bij jest równe liczbie spacerów długości k o początku w i oraz końcu w j.

Korzystając z tego twierdzenia rozwiąż poprzednie zadanie w przypadku k = 2 i k = 3.

Zadanie 7.6. Dany jest graf G o 12 wierzchołkach i 56 krawędziach.

a.    Ile najmniej i najwięcej składowych może mieć G?

b.    Ile najmniej i najwięcej składowych może mieć G^c?

Odpowiedz na powyższe pytania w przypadku, gdy dodatkowo założymy, że graf G ma minimalny stopień większy od 1

Zadanie 7.7. Odpowiedzi krótko uzasadnij

(a)    Ile krawędzi ma dopełnienie grafu prostego na 9 wierzchołkach i o 22 krawędziach ?

(b)    Co możesz powiedzieć o prostym grafie o 3 składowych spójności, w którym mamy dokładnie 2 wierzchołki stopnia 1 a pozostałe wierzchołki są stopnia 2 ?

(c)    Narysuj wszystkie nieizomorficzne spójne grafy proste na czterech wierzchołkach.

(d)    Narysuj graf prosty na 5 wierzchołkach, który jest grafem Hamiltona a nie jest grafem Eulera.

(e)    Ile jest drzew na zbiorze wierzchołków {1,2,3,4,5,6,7,8}, dla których wierzchołek 2 ma stopień 6 ?

Zadanie 7.8. Udowodnij, że w każdym grafie na n wierzchołkach istnieją co najmniej dwa wierzchołki o tym samym stopniu.

8 Drzewa

Zadanie 8.1. Udowodnij indukcyjnie, że w każdym drzewie na n, n ^ 2, wierzchołkach istnieją co najmniej dwa wierzchołki o stopniu jeden.

Zadanie 8.2. Narysuj wszystkie nieizomorficzne drzewa na siedmiu wierzchołkach o maksymalnym stopniu rów-Zadanie 8.3. Korzystając z tw. 7.10 lub tw. 7.11 znajdź liczbę drzew rozpiętych grafów podanych poniżej.

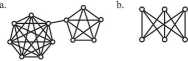
Zadanie 8.4. Ile jest różnych drzew o zbiorze wierzchołków {1,..., 12} i ciągu stopni podanym poniżej (wskazówka: skorzystaj z kodu Priifera)

a.    (4,4,4,2,1,1,1,1,1,1,1,1)?

b.    (5,3,2,2,2,2,1,1,1,1,1,1)?

Odpowiedź uzasadnij.

Zadanie 8.5. Graf G ma 225 rozpiętych drzew. Po usunięciu pewnej jego krawędzi e okazało się, że graf G — e ma już tylko 25 drzew rozpiętych. Niech G’ będzie grafem otrzymanym z grafu G przez podział krawędzi e nowym wierzchołkiem. Ile drzew rozpiętych ma G* ?

4