3545336582

Zakładając stałe wartości k_d,p,c,k z równania (3) można obliczyć wzrost temperatury

przewodu ponad temperaturę otoczenia:

9-9_<:

... k_d ■ p

a-S-c

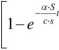
a-S

+ (9_p-9J-e ")

(4)

przy czym: t - czas od chwili rozpoczęcia obserwacji przebiegu nagrzewania [s]; 9_P - temperatura początkowa przewodu w chwili rozpoczęcia obserwacji [°C]; 9 - temperatura przewodu po czasie t [s].

Wyrażenie

a-S

we wzorze (4) ma wymiar czasu i nazywane jest cieplną stałą czasową T.

Wobec tego, że T> 0, wyrażenie    dąży, w miarę upływu czasu, do zera, a

temperatura 9 przewodu dąży do wartości ustalonej & = przy czym

(5)

Po podstawieniu równania T = cs/aS i wyrażenia (5) do wzoru (4) otrzymuje się równanie krzywej nagrzewania:

(6)

9 ₌ S_u-(9_u-9_r)e^^ri

Zawarta w równaniu (6) temperatura ustalona zależy od temperatury otoczenia. Dla każdej temperatury otoczenia otrzymamy inną krzywą & = f(t) o rzędnych przesuniętych w górę lub w dół o tą samą wartość. Z zależności (6) można usunąć temperaturę otoczenia wprowadzając przyrosty temperatur: x -    x_M = &„ - S„. Otrzymujemy wówczas równanie nagrzewania dla

dowolnej temperatury

lub

1-e ^T>

(7)

(8)

w którym: x_p - początkowy przyrost temperatury przewodu ponad temperaturę otoczenia [°C],