5555241348

3

3

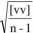
= ±0.035m

■ błąd średni pojedynczego spostrzeżenia m = ±

■ błąd średni średniej arytmetycznej M = ±-7= = ±0.01 lm

Vn

rys.l

■ ok.68% spostrzeżeń zawiera się w granicach błędu średniego ±m., czyli odchylenia standardowego (a ) zgodnie z rozkładem normalnym Gaussa (dla naszego przykładu od 182.064m. do 182.'"'    '    ■    •    •

I

Wypada jeszcze nadmienić za [11], że MNK wprowadził w 1806 r. Legendre i niezależnie w 1808 r. Gauss , z tym że w [8] autor podał iż C.F. Gauss opracował metodę w 1794 roku, a opublikował 1809, a ponadto że wprowadził ją również w 1802 Laplace. Jak widać występują tutaj pewne rozbieżności, chyba dla istoty zagadnienia niekoniecznie najważniejsze. Najistotniejsze powinno być dla nas to, że niekwestionowany autorytet w zakresie obliczeń geodezyjnych, nazwany pięknie przez prof. Z. Adamczewskiego we wspomnieniu [2]-wirtuozem geodezyjnego rachunku- Profesor Stefan Hausbrandt już w 1922 roku uzasadniał celowość wyrównań ścisłych. Wtedy i na wiele lat później barierą w stosowaniu MNK była pracochłonność, dzisiaj ten argument jest zamierzchłą historią, a my jak jeden mąż możemy wcielić w życie postulat wirtuoza geodezyjnego rachunku.

2.2 Narzędzia do realizacji MNK.

Literatura zna dwa podstawowe narzędzia do realizacji postulatów MNK, a mianowicie :

■    metodę pośredniczącą ,nazywaną również metodą parametryczną

■    metodę zawarunkowaną, nazywaną też metodą korelat

Obydwie natomiast wymienione powyżej metody nazywa się ścisłymi w odróżnieniu od metod przybliżonych, którymi np. wyrównuje się jedną z klasycznych konstrukcji jaką jest ciąg poligonowy w pełni dowiązany dwustronnie, gdzie najpierw wyrównuje się kąty a później przyrosty współrzędnych. O wyborze metody ścisłej : pośredniczącj czy zawarunkowanej decydowała kiedyś głównie ilość równań normalnych pierwszej z nich, lub równań normalnych korelat drugiej co analizuje szczegółowo autor w [9] .Postępy w informatyce sprawiły, że od dawna praktycznie stosuje się metodę pośredniczącą! 10]zob.str.382.

3.Metoda pośrednicząca

Istota tej metody polega na tym, że do wyznaczenia pewnych niewiadomych, najczęściej współrzędnych punktów X i y , które nie mogą być wyznaczone bezpośrednio służą nam wielkości dostępne jak np. kąty (kierunki), odległości, rzadziej azymuty. Rozważmy teraz sieć