5851989581
|
. cos5x g),h-ą^ |
e3* — 1 h) lim . ^—: x—*o sm2x |
i) lim1“(1 + ^); x-0 X | |
|
lim + | |||
|
m).‘!S.(1 + rT2) 1 |
m) Hm [1 + tg(2x)]ct |
g*. |
. v^l + x - v^l — X o) lun-. x—*0 X |
|
6.6. Znaleźć asymptoty pionowe i ukośne funkcji: | |||
|
l-x2 | |||
|
b)f(X> (x+l)2’ |
X+1 ’ | ||
|
1 | |||
|
e* — r | |||
|
g) /(*) = |
. V ,, . sin2 x h) /(*) = —gg~\ |
i) /(*): |
= x — arc tg x. |
Lista 7
7.1. Narysować wykresy funkcji spełniających wszystkie podane warunki:
a) lim f(x) = oo, lim f(x) = 1, /(2) = 0, lim f(x) = —1;
b) lim f(x) = e, lim f(x) = 0, funkcja / jest parzysta;
c) prosta y = x + 1 jest asymptotą ukośną funkcji / w —oo, prosta y = x — 1 asymptotą ukośną w oo, a prosta a: = 0 jest jej asymptotą pionową obustronną;
d) lim f(x) — 0, lim /(x) — 3, lim f(x) — —oo;
e) /(m) = oo, lim_ /(x) = -oo, lim+ /(x) = 1, Jfrn^ /(x) = 5;
f) lim f(x) = —4, lim ^ /(x) = oo, lim /(x) = 4;
g) lim /(x) = oo, lim f(x) = 0, funkcja / jest okresowa i ma okres T = 3;
h) lim f(x) = 4, lim /(x) = oo, funkcja / jest nieparzysta.
Na rysunkach wskazać fragmenty wykresów spełniające poszczególne warunki.
7.2. Dobrać parametry a, b € R tak, aby podane funkcje były ciągle na R:
a) f(x) =
d) f(x) =
j — + 1 dla x < —1,
\ b — 2x dla x > —1;
{x2+ax+b dla |x| < 2, x\Jx2 — 4 dla |x| > 2;
b) f(x) =
sinx dla |x| > —,
; c)/(x) = ax + 6 dla |x| < —;
bx dla x <ir, SUia: dla x > ir.
f) /(x)=
{ax2 + 1 dla x < -1,
2x dla -1 < x < 0, x3 + bx dla x > 0; f a sin x + 6 cos x dla |x| >
| 1 + tgx dla |x| < j.
7.3. Określić rodzaje nieciągłości funkcji w punkcie a (jeżeli istnieją) dla funkcji o podanych wykresach:
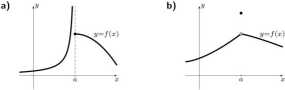
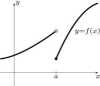
Wyszukiwarka
Podobne podstrony:
image065 lim x„ = ę n-Jra
Image1911 • lim x-»-« = sgn CO x2 -4 (~x?-4 x2 -4 iczniki mianownik są wielomianam
Image1922 lim 1 X-»TOx +3 lim X-»" -2x"= lim X—> “ -2x + 3, x+3 “2 x+3 x + 3 o X- =
Image1933 lim f(x) < lim g(x) X—źXq X—^ Xq
s22 23 22 sin2(§) sin2(2x) 25. lim 21 V ’ 27. lim x—>o 3x4 2x — arcsin x 26. li
IMG 29 i Zadania 1 c) lim (cos x) x ; ... x — arctgrr e) lim- *->0 x2 d) lim x arc ctgz; X—►OO
153 (2) Ij. Granica i ciągłość funkcji jednej zmiennej n) lim X—►() a/ 1 + X + X2 — 1 o) lim y/x2 +
gf1 Rozdział 22. Obliczyć granice funkcji w punkcie:a) lim x—>2c)
gf3 Rozdział 24. Obliczyć: a) lim (x3 - 2x2 - x + 1) =lim x3(l x—’►«> e)
gf5 Rozdział 2 lim 2 <**i> = ^2 x—*■! 6. Obliczyć: a) lim 2*2-i =lim 2 X—*1
heinego Liczba g jest granicą funkcji /w punkcie x0, jeżeli V(x„)„eN : lim x„ = x0 =>lim f(xn) =
lim /(1) = g » a [(lim .x„ = x0 ] => (lim /(1„) = g
więcej podobnych podstron