8416074015

Modelowanie Cyfrowe - laboratorium

2.4. Algebra liniowa

Przykład 2.14

Rozwiąż układ równań liniowych:

f 2x_{ + x₂ = 1 [3*, + 2x₂ = 0

Układ ten można zapisać w postaci macierzowej AX = B gdzie:

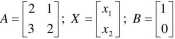
Dla której rozwiązanie ma postać:

X = A B

» A= [2 1; 3 2]

A =

2    1

3    2

» B= [1; 0]

B =

1

0

» X=inv(A)*B X =

2.0000

-3.0000

Uwaga!: Zagadnienie to można rozwiązać także korzystając z dzielenia prawo na lewo

» X=A\B

Matlab - Simulink 15