082 2

162

0)

IX. Macierze, wyznaczniki, równania liniowe

Zadanie 9.12. Rozwiązać układ równań

2x — 4y+ Sz-6u = 7, 5x-10y + 20z    =12,5.

Rozwiązanie. Rząd macierzy współczynników

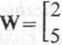
-4 8 -61

-10 20 oJ

wynosi r(W)=2, gdyż np. minor utworzony ze współczynników przy x i u

2

5

-6

0

= 30#0 ,

oraz rząd macierzy uzupełnionej U wynosi r(U) = 2, gdyż ten sam minor występuje w macierzy U. Zatem r(W) = r(U).

Układ jest więc rozwiązalny. Przenosimy niewiadome nie objęte obliczonym minorem, tzn. niewiadome y, z, na prawą stronę:

2x —6w = 7    + 4y- 8z ,

5x    =12,5 + 10y —20z

i rozwiązujemy ten układ traktując y i z jako parametry. Z twierdzenia Kroneckera--Capelliego wiemy, że rozwiązania będą zależne od n — r — 4 — 2 = 2 parametrów y i i Układ (2) można rozwiązać prościej bez pomocy wzorów Cramera. Mianowicie z drugiego równania obliczamy

(3)    x = 2,5+2y-4z ,

a następnie z pierwszego równania obliczamy

«=-ł-

Tak więc w naszym układzie y, z mogą przybierać wartości zupełnie dowolne niezależny od siebie, u przyjmuje tylko jedną wartość — a wartości x są ściśle uzależnione wzorem ( od nadanych wartości zmiennym y, z.

Zadanib 9.13. Rozwiązać układ czterech równań z trzema niewiadomymi:

5x + 3y- z = 3 , 2x+ y- z = 1 ,

3x —2y +2z= —4 , x- y + 2z= —2 .

r

§ 9.6. Ogólny uktad równań liniowych

163

Rozwiązanie. Macierz współczynników

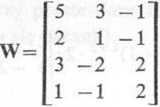
może być co najwyżej rzędu 3, natomiast macierz uzupełniona

5    3 -1    3'

u- ²    1 -¹    1

3-22-4 1-1 2-2

może być rzędu co najwyżej 4. Gdyby okazało się, że r(U)=4, od razu wnioskowalibyśmy, wobec r(W)#r(U), że układ jest sprzeczny. Ustalmy więc najpierw rząd macierzy U. Aby obliczyć wartość wyznacznika det U, do wyrazów drugiej kolumny dodajmy wyrazy trzeciej kolumny:

5 2	-1	3
2 0	-1	1
3 0	2	-4
1 1	2	-2

a następnie do wyrazów czwartej kolumny dodajmy wyrazy trzeciej kolumny:

detU =

5 2	-1	2
2 0	-1	0
3 0	2	-2
1 1	2	0

Następi

nie rozwińmy otrzymany wyznacznik według elementów drugiej kolumny:

detU=( —i)^{ł +} 2 -2

~ —2•( —1)² + 3 -( — 2)

2	-1	0		5	-1	2
3	2	-2	+(-l)^4 + 2-l-	2	-1	0
1	2	0		3	2	-2

+(-l)

r + 3.

2 -1 1 2

2 -1 3    2

+ (-l)^{3 + 3}-(-2)

5 -1 2 -1

ĄtyjęC

Sad;

= -4(4 + 1) +2-(4 + 3) —2( —5+2)= -20 + 14 + 6 = 0. rząd r (U) <4.

j_ej|j ^amy dalej rzędy macierzy W i U. Celowe jest badanie rzędu macierzy W. gdyż Jest °^kazałoby się, że r(W) = 3, to również r(U) = 3, ponieważ każdy minor macierzy W kdrtocześnie minorem macierzy U.

6»