091

180 IX. Macierze, wyznaczniki, równania liniowe

180 IX. Macierze, wyznaczniki, równania liniowe

9.26.

9.27.

2 1 4 3 5 3

5    6 8 7 4 2 8 9 7 6 0 0 2 3 5 4 0 0 4 3 0 0 0 0

6    5 0 0 0 0

7 6 5 ^42 9 7 8 9 3 3 7 4 9 7 0 0 5 3 6 1 0 0 0 0 5 6 0 0 0 0 6 8 0 0

9.28.

2	3	0	0	1	-1
9	4	0	0	3	7
4	5	1	-1	2	4
3	8	3	7	6	9
1	-1	0	0	0	0
3	7	0	0	0	0

Nie rozwijając wyznaczników wykazać, że przy dowolnych wartościach liczbowym a, b, c, m, n, p, r, s, t zachodzą równości (zad. 9.29 - 9.30):

a — b	m — n	r — s			a	b+c	m
b-c	n-p	s-t	= 0.	9.30.	b	c+a	m
c — a	p — m	t-r			c	a+b	m

Obliczyć wyznaczniki (zad. 9.31 - 9.34):

	2	1 2	3	2				3	4	-3 -1	2
	3	-2 7	5	-1				-5	6	5 2	3
9.31.	3	-1 -5 -	-3	-2	.		9.32.	4 -	9	-3 7	-5
	5	-6 4	2	-4				-1 -	4	1 1	-2
	2	-3 3	1	-2				-3	7	5 2	3
	1	1 1 0	0
	1	2 3 0	0
9.33.	0	1 1 1	1
	0	*2 ^x3	x4
	0	2 2 2 XI X2 X3	xl
	011 012		013			• 01,2/1 — 2	01,2/1-1	01, 2/i
	0	022	023			• 02,2/1-2	^fl2, 2n-l	0
	0	0	033		.	• 03,2/1-2	0	0
9.34.
	0	0	a	2n — 2	3 •	• 02//-2.2/I-2	0	0
	0	02/1—1,2	02n-l,3 •			•• 02/1-1,2/1-2	02n-l, 2/1-1	0
	02n, 1 02n, 2		02/., 3			• 02n,2n-2	02/1, 2n-l	02/1, 2/1

Rozwiązać następujące układy równań (zad. 9.35 - 9.38):

9.35. 2x — 3y = 3, x+2y=5.    9.36. 6x-4y = 5, 9x - 6y=2.

9.37. 3x + 5y = 5, x-2y = 9.    9.38. 2x-4y = 10, 5x-10j'=^2:’'

Rozwiązać i przedyskutować w zależności od parametru k następujące układy tó^w°^afl (zad. 9.39 - 9.40):

9.39.    (fc — 2) x +(2 — fc) y = 3fc — 6, (2fc²-8)x-(3/c-6)y = 10-5fc.

9.40.    fcx+4y = 2fc, 9x+fcy=18.

Rozwiązać następujące układy równań (zad 9.41 - 9.44):

9.41.    x+2y + 3z = 14, 3x+y+2z = ll, 2x + 3y+z = ll.

9.42.    2x-y+z=l, 3x+y-2z = 0, x-3y-z = 2.

9.43.    5x-3y+2z = 3, 4x + 5y-3z = 21, 5x-2y-3z = -12.

9.44.    3x + 12y + 5z+43 = 0, 5x —3y-10z+76 = 0, 4x —17y+2z —23=0.

Rozwiązać następujące równania jednorodne (zad. 9.45 - 9.46):

9.45. 4x —3y = 0    9.46. 2x+5y — 4z = 0.

Rozwiązać i przedyskutować w zależności od parametru k równania jednorodne (zad. 9.47 - 9.48):

9.47. (k — 2)x +(12 — 3/c²)y = 0.    9.48. (k-5)x-3y = 0.

Rozwiązać następujące układy równań jednorodnych (zad. 9.49 - 9.56):

9.49. 4x-6y = 0, 6x-9y = 0.    9.50. 2x+3y = 0, 3x-5y = 0.

9.51. fcx+9y = 0, 4x + fcy = 0.    9.52. 2x-/cy = 0, fcx+4y = 0.

9.53.    2x —12y+6z = 0, 5x —30y+ 15z = 0.

9.54.    4x-6y + 10z = 0, 6x-9y-15z = 0.

9.55.    2x —4y = 0, 5x-10y = 0, 3x + 5y = 0.

9.56.    4x —6y = 0, 6x-9y = 0, 2x-3y = 0.

Rozwiązać następujące układy równań (zad. 9.57 - 9.66):

9.57.    2x + 5y-8z = 8, 4x + 3y —9z = 9, 2x + 3y —5z = 7, x+8y —7z = 12.

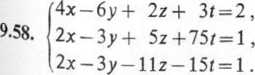
x+ y+3z — 2t+3u = l, 9.6o. ^2x+2y+4z- t +3u = 2,

3x + 3y + 5z — 2f + 3u = 1, 2x + 2y + 8z — 3f + 9u = 2.

x + 2y + 3z-2t + u=4, 3x + 6y + 5z - 4t + 3w = 5, x+2y+7z-4t+ w=11 2x + 4y + 2z — 3f 4- 3« = 6.

3x +2y +2z +2t = 2, 2x + 3y + 2z + 5f = 3,

⁹‘⁶²' 9x+ y +4z —5/ = l,

2x+2y + 3z+4f = 5, 7x+ y+ 6z— r = 7.

7x + y +6z —

8x + 6y + 5z +2t — 21, 3x+3y + 2z+ t = 10,

9.63.    4x+2y+3z + t= 8,

3x + 5y+ z+ t = 15, 7x+4y + 5z+2ł = 18.