088 2

174 IX. Macierze, wyznaczniki, równania liniowe

Nietrudno jest wyprowadzić następujące wnioski z podanych aksjomatów:

1. Jakiekolwiek weźmiemy dwa elementy przestrzeni liniowej a i b, to zawsze 0 _a_ =0 b. Ten element przestrzeni liniowej X równy 0 a, gdzie a jest dowolnym eleine_nt_ei)) przestrzeni X, nazywamy elementem zerowym przestrzeni X (lub krótko: zerem przestrój X) i oznaczamy symbolem 0. Łatwo wykazać, że dla każdego elementu b przestrzeni X zachodzi równość b+0=b.

2.    Jakikolwiek weźmiemy element a przestrzeni X, to mamy a+(-l)a=0. Element (-l)a nazywamy elementem przeciwnym do elementu a i oznaczamy symbolem L_a

3.    Równanie a+x=b, gdzie a i b oznaczają dane elementy przestrzeni X, natomiast x oznacza taki poszukiwany element przestrzeni X, dla którego zachodzi podana równość ma zawsze dokładnie jedno rozwiązanie: *=£>+( — l)o. Stąd wynika, że w przestrzeni liniowej można zawsze określić w sposób jednoznaczny operację odwrotną do operacji dodawania, którą nazywamy operacją odejmowania, a którą określamy w następujący sposób: a—b=a+(-\)b.

W analogiczny sposób jak przestrzeń liniową nad ciałem liczb rzeczywistych definiuje się przestrzeń liniową nad ciałem liczb zespolonych.

Czytelnik może sam łatwo udowodnić, że zbiór wszystkich macierzy ustalonego wymiaru mxn przy działaniach określonych wzorami (9.7.1) i (9.7.3) jest przestrzenią liniową nad ciałem liczb zespolonych.

Weźmy teraz z kolei pod uwagę zbiór wszystkich macierzy kwadratowych pewnego ustalonego stopnia n. W zbiorze tym oprócz działań dodawania elementów i mnożenia elementu przez liczbę możemy wykonywać działanie mnożenia elementów tego zbioru przy użyciu wzotu (9.7.4). Przy tak określonych działaniach zbiór wszystkich macierzy kwadratowych ustalonego stopnia n jest pierścieniem liniowym. Podajmy ogólnie definicję pierścienia liniowego.

Pierścieniem liniowym nad ciałem liczb rzeczywistych (zespolonych) nazywamy zbiór r. który jest przestrzenią liniową nad ciałem liczb rzeczywistych (zespolonych) i w którym jest określona dodatkowo

c) operacja mnożenia elementów zbioru P w ten sposób, że oprócz siedmiu aksjomatów przestrzeni liniowej są spełnione następujące dodatkowe aksjomaty:

8° (ab)c = a(bc), czyli mnożenie elementów jest łączne,

9° a(b+c)=ab+ac, czyli mnożenie jest rozdzielne względem dodawania lewostronnie. 10° (a+b)c=ac+bc, czyli mnożenie jest rozdzielne względem dodawania prawostronnie-

Natomiast mnożenie elementów pierścienia jest na ogół nieprzemienne, tzn. na og® jest abi=ba.

Jednością pierścienia nazywamy taki element pierścienia e, że dla dowolnego elenien¹® pierścienia a zachodzi równość ae=ea=a. Pierścień liniowy może (ale nie musi) posia jedność.

Czytelnik sam udowodni, że zbiór wszystkich macierzy kwadratowych ustalon®^ stopnia « przy działaniach określonych za pomocą wzorów (9.7.1), (9.7.3) i (9.7.4) J pierścieniem liniowym nad ciałem liczb zespolonych z jednością, którą jest macierz jed®® kowa I„ (patrz str. 166).

§ 9.8. ZAPIS MACIERZOWY UKŁADU RÓWNAŃ LINIOWYCH

Wykorzystamy obecnie nasze wiadomości o macierzach do układów równań liniowych. Zauważmy, że układ n równań liniowych (jednorodnych albo niejednorodnych)

, _n niewiadomymi

a_lix₁+a₁₂X2+...+a_lnx_H=b₁, a_2lx₁+a₂₂x₂ + ... +a_2n x„=b₂,

(9.8-0

^anl^xl+a„₂ X₂ + ... + ^am^x„ = b_n,

może być zapisany w tzw. postaci macierzowej

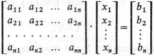
(9.8.2)

Oznaczając macierz współczynników przez W, macierz kolumnową niewiadomych przez X, a macierz kolumnową wyrazów wolnych przez B, możemy zapis układu (9.8.1) lub równoważny mu zapis macierzowy (9.8.2) ująć krótko:

(9.8.3)    WX=B.

Pomnóżmy równanie (9.8.3) lewostronnie przez macierz W^-1 (przy założeniu, że macierz W jest nieosobliwa, tzn. det W^O), tzn. przez macierz odwrotną względem macierzy współczynników W, obie strony tego równania macierzowego; otrzymujemy (9.8.4)

Ale według (9.7.10) W^_,W = I, a według (9.7.6) IX = X, więc (9-8.5)    X=W-'B.

Jest to rozwiązanie układu (9.8.1) (przy założeniu, że wyznacznik współczynników det W?s0) w postaci macierzowej.

Otrzymane rozwiązanie (9.8.5) jest oczywiście identyczne z rozwiązaniem za pomocą Azorów Cramera (9.4.3), ale w znacznie prostszej postaci.

§ 9.9. PRZEKSZTAŁCENIA LINIOWE

k Powróćmy do układu n równań liniowych (9.8.1) z n niewiadomymi z tą różnicą, Prawe strony tych równań będziemy traktowali jako zmienne, dlatego oznaczmy je przez

........

a_llx_l+a₁₂x₂ + ... +ai„x„ = y₁,

(9-9.li

'    ^an^xi+‘^I22x₂ + ...+a_2nx_n = y₂,

.=>»•

,,x,+a„ ₂ x₂ + ...+a„