093 2

184 XX. Macierze, wyznaczniki, równania liniowe

184 XX. Macierze, wyznaczniki, równania liniowe

1	2	3	4 ..	. n — 1	n
0	1	2	3 .	. n — 2	n-1
0	0	1	2 .	co 1 c	n—2
0	0	0	0 .	. i	2
0	0	0	0 .	. 0	1

9.100.

Rozwiązać równania macierzowe (zad. 9.101 - 9.103):

r-^12i.	9.102. r* 91
L-^56J	L^6 9J

f3 6"| [2 4" 9.103. X- _{4 g} - _{9 lg}J-

BADANIE PRZEBIEGU ZMIENNOŚCI FUNKCJI

§ 10.1. TWIERDZENIA ROLLE A I LAGRANGE’A

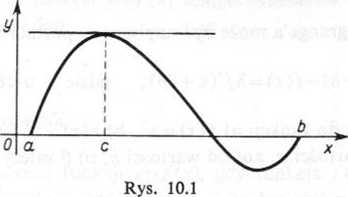
(10.1.1) Twierdzenie Rolle’a. Jeżeli funkcja f(x) jest ciągła w przedziale a^x^b i jest różniczkowalna wewnątrz tego przedziału, przy czym f (a) = 0, f(b) = 0, to istnieje co najmniej jeden punkt wewnętrzny tego przedziału x = c taki, że pochodna w tym punkcie f’(c) jest równa zeru:

/'(c) = 0    (a<c<b).

Geometrycznie oznacza to, że istnieje co najmniej jeden punkt wewnętrzny taki, że styczna w tym punkcie krzywej jest równoległa do osi Ox (rys. 10.1).

m-m

b-a

=/'(c)