22064 MATEMATYKA189

368 Vn. Macierze. Wyznaczniki. Układy równań liniowych

368 Vn. Macierze. Wyznaczniki. Układy równań liniowych

	'2	0	4	0	1		'2	0	1
R(B)* R	0	1	0 -1		0	= R	0	1	0
	1 -1		2	1	°J		1 -1		0

= 3.

Ponieważ R(A)*R(B), więc, zgodnie z twierdzeniem Kroneckcra-Capcllicgo, układ ten nic ma rozwiązań.

b) Dla danego układu

x-y+2u	- 0,
2x + y + 3z + u + 3v	= 3,
X + Z + U + V	- l;

(1)

obliczamy rzędy macierzy A i B:

R(A) = R

l -1	0	2	0"		1	-1	0	2
2 I	3	1	3	= R	2	1	3	1
1 0	1	1	1		ł	0	I	1

(tworzymy zera w 1-ej kolumnie] przy pomocy 1-ego wiersza J

•ii -j ; Jb

R(B)=R

1-10200 2    13 13 3

1 0 1111

{po opuszczeniu 6- tej kolumny 1 ₌ Rz a ) —2 otrzymamy macierz A

Mamy zatem R(A)=R(B) = r=2, n = 5, czyli ren. Z twierdzenia Kroncckera - Capclliego wynika, źc układ ten ma nieskończenie wiele rozwiązań i są one zależne od n - r = 3 parametrów.

Aby znaleźć rozwiązania w takim przypadku należy' spośród równań układu (1) wybrać r ró\Vnań o r niewiadomych (pozostałe niewiadome traktujemy jako parametry) w ten sposób, aby wyznacznik główny otrzymanego układu pomocniczego (2) był różny od zera. (Jest to możliwe, gdyż R(A) = r, a to oznacza, że istnieje minor stopnia r macierzy A różny od zera). Układ (2) ma , zgodnie z twierdzeniem Cramera, dokładnie jedno rozwiązanie. Wykazuje się, że rozwiązanie układu (2), uzupełnione przez parametry, jest rozwiązaniem układu (1).

W naszym przykładzie przyjmijmy z = z₀,u = u_o,v = v_o i z dwóch pierwszych równań danego układu utwórzmy pomocniczy układ z niewiadomymi x i y:

W»|]    =0*0.

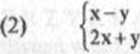
“ -2u₀.

= 3-3/.o -Uq -3v₀,

Rozwiązaniem układu (2) jest para liczb:    x*l-Zfl-u₍₎ -v₀,

y s 1- zo + u₀ - v₀. Natomiast rozwiązaniem danego układu (1) jest każda

piątka liczb:    x = 1-zo-u₀-v₀, y = l-Zo+uo-v₀, ^/m/o ^{u = u}o»

v - v₀, gdzie z₀.u₀,v₀ są dowolnymi liczbami rzeczywistymi.

c) Dla danego układu

2x+y »	1.
x + y =	1,
x-2y *	-2.
2x-y =	-1

(1)

obliczamy rzędy macierzy A i B:

R(A) = R	2 1 1 1 1 -2	= 2, R(B)= R	2 1 1 1 1 1 1 -2 -2	= R	2 I 1 1 1 -2
	2 -1		2 -1 -1		2 -1

Mamy więc R(A) = R(B) = r = 2, n = 2, czyli r = n. Z twierdzenia Kroneckera - Capcllicgo wynika, że rozpatrywany układ równań ma dokładnie jedno rozwiązanie.

Aby znaleźć to rozwiązanie w takim przypadku należy spośród równań danego układu (I) wybrać r równań o r (r = n) niewiadomych w ten sposób, aby wyznacznik główny otrzymanego układu pomocniczego (2) był różny od zera (wiemy już, że to jest możliwe, gdyż R(A) = r). Zgodnie z twierdzeniem Cramera układ (2) ma dokładnie jedno rozwiązanie. Wykazuje się, że jest to jednocześnie rozwiązanie układu (1).

W naszym przykładzie - utwórzmy układ pomocniczy (2) z dwóch pierwszych równań układu (1):

(2)

2x + y x + y

I.

I

W =

2 1 1 1

* 0 .

Rozwiązaniem układu (2), a zatem i rozważanego układu (1), jest para liczb: x = 0, y = I.