090

178 IX. Macierze, wyznaczniki, równania liniowe

Gdy macierz A jest macierzą ortogonalną, wówczas

(9.10.5)    AA^t = AA~‘=I oraz A^TA = I.

Z tych równości wynikają następujące własności macierzy ortogonalnej:

(9.10.6)    Suma kwadratów wszystkich elementów dowolnego wiersza oraz dowolnej kol_Urni[ macierzy ortogonalnej równa się 1, tzn.

aft + af₂ +...+af_n=l    dla i = l,2,...,n

oraz

°i*+°2Jr + --- +^ank ⁼ 1 dla k=],2,...,n.

(9.10.7) Suma iloczynów wszystkich, odpowiednich elementów dwóch różnych wierszy oraz dwóch różnych kolumn macierzy ortogonalnej równa się zeru, tzn.

fl/i a_jl+a_i2aj₂+...+a_ina_jn = 0 dla i*j, i,j=l,2,..., n

oraz

a_]ka_u + a_2ka_2l + ...+a_nka„, = 0    dla k^l,k,l = 1,2.....n.

Czytelnik zechce sprawdzić te własności na przykładzie macierzy ortogonalnej W określonej wzorem (9.10.1).

Na koniec zauważmy, że z równości (9.10.5) wynika równość dotycząca wyznaczników:

det A-det A^T = detI,

ale detA^T=detA, det 1=1, więc (detA)² = l, skąd

(9.10.8)    det A = +1.

Wykazaliśmy więc, że wyznacznik macierzy ortogonalnej może być tylko równy +1 albo — 1.

§ 9.11. RÓWNANIE CHARAKTERYSTYCZNE (WIEKOWE) MACIERZY

Z danej macierzy kwadratowej A stopnia n o elementach a_ik (i, k = 1, 2,.... ń) utwórzmy nową macierz, odejmując zmienną X od wszystkich wyrazów położonych na przekątnej głównej, a pozostałe wyrazy pozostawiając bez zmiany; otrzymujemy nową macierz Przyrównując do zera wyznacznik tej macierzy

et 11 k	a 12	• aln
^a21	#22 — ^	■ a2n
ani	a„ 2	•• ^ann~

(9.11.1)

otrzymujemy równanie stopnia n względem X, które nazywamy równaniem tycznym (lub wiekowym) macierzy A. Pierwiastki tego równania, różne od zera óla cierzy nieosobliwej, nazywamy wartościami własnymi macierzy A.

Zadanie 9.21. Znaleźć wartości własne macierzy

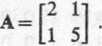
Rozwiązanie. Tworzymy równanie charakterystyczne tej macierzy

2-a 1 1    5 —A

= 0,

skąd

(2—A) (5 — A) —1=0, czyli A²-7A+9=0.

ponieważ ,4 = 49-36= 13>0, więc równanie charakterystyczne ma dwa pierwiastki rzeczywiste    _    _

A, = ±(7-Vl3), A₂ = d(7+Vl3).

Są to wartości własne macierzy A.

Zadanie 9.22. Sprawdzić, że macierz A z poprzedniego zadania jest pierwiastkiem macierzowym swojego równania charakterystycznego.

Rozwiązanie. Mamy wykazać, że spełnione jest równanie macierzowe

A² —7A+9I=0,

gdzie I oznacza macierz jednostkową, a O — macierz zerową. Wykonajmy działania na macierzach po lewej stronie ostatniego wyrażenia:

A=—7A₊9I-(j |]-p j]-7-p ;]+9-[J ?]-

2-2 + 1 • 1 2-1 + 1' 2 + 5-1 1-1+5'

14H5 ?H? o]-

godnie z treścią zadania. Nie jest to bynajmniej przypadek, zachodzi bowiem następujące Sierdzenie Cayley-Hamiltona:

^•11.2) Dowolna macierz kwadratowa jest pierwiastkiem swego równania charakterystycznego.

Zadania

1	3	4	5		0	5	0	2		0	a	b	c
3	0	0	2	9.24.	8	3	4	5	9.25.	1	X	0	0
5	1	2	7		7	2	1	4		1	0	y	0
2	0	0	3		0	4	0	1		1	0	0	z

Obliczyć wyznaczniki (zad. 9.23 - 9.28): 9.23.

I