086

170 IX. Macierze, wyznaczniki, równania liniowe

Można wykazać ogólnie, że dla dowolnej macierzy A zachodzą związki

(9.7.6)    AI=A oraz IA=A.

W obu równościach I oznacza macierz jednostkową, ale w każdej z tych dwóch rów ności I może być macierzą innego stopnia.

Uwaga. Macierz jednostkowa przy mnożeniu macierzy spełnia więc analogiczną rolę jak liczba jeden przy mnożeniu liczb:

a • 1 = a oraz    1 • a = a.

Zadanie 9.18. Znaleźć iloczyn macierzy

A =

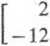
-4

6

B =

1 2

5    10

6    12

*o.

Rozwiązanie. Macierz A jest wymiaru 2 x 3, a macierz B wymiaru 3x2, więc iloczyn jest wykonalny; w wyniku otrzymamy macierz typu 2x2, tzn. macierz kwadratową. Stosujemy schemat Falka

1 2 5 10

_; 6 12

’ 2 -4    3    0    )

-12    6 -3    0 0

a więc AB = 0.

Otrzymaliśmy interesujący wynik, mianowicie, że iloczyn dwóch macierzy niezerowych może być równy macierzy zerowej.

Uwaga. Analogiczna własność dla iloczynu dwóch liczb nie zachodzi, mianowicie iloczyn dwóch liczb, z których żadna nie jest zerem, nie może się równać zeru.

Natomiast inną własność analogiczną do własności iloczynu liczb ma iloczyn dwóch macierzy:

(9.7.7) Iloczyn dwóch macierzy, z których przynajmniej jedna jest macierzą zerową-równa się macierzy zerowej:

A0=0 oraz 0A = 0.

Zwróćmy uwagę na fakt, że każdy z czterech symboli O macierzy zerowej może ozna czać inną macierz zerową.

Zadanie 9.19. Pomnożyć macierz A przez macierz zerową O, gdzie

A=

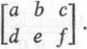
by*⁴

Rozwiązanie. Ponieważ macierz A jest wymiaru 2x3, więc aby mnożenie wykonalne, jako macierz zerową trzeba przyjąć macierz wymiaru 3 x k, gdzie k

kolumn) może być dowolna: k= 1,2, ... Mamy

	k kolumn
	0 0 ... 0 0 0 ... 0 0 0 ... 0
a b c d e f	0 0 ... 0 0 0 ... 0

, _więc AO = O, ale macierz O z lewej strony tej równości jest typu 3 x k, a macierz O z prawej strony jest typu 2xk.

Iloczyn macierzy przez macierz, przy założeniu, że wszystkie działania poniżej użyte _są wykonalne, ma własność łączności, tzn.

(9.7.8)    (AB) C=A (BC) = ABC,

oraz własność rozdzielności (zarówno względem dodawania jak i odejmowania), tzn.

(9.7.9)    (A±B)C = AC±BC, C(A±B) = CA±CB.

Weźmy macierz kwadratową A = [a,*] (/', k= l, 2, ..., n); jeśli dopełnieniem algebraicznym elementu a_ik (patrz § 9.1) jest A_ik (/, k= l, 2.....ń) i zamiast każdego elementu

macierzy A umieścimy jego dopełnienie algebraiczne A,_k, a następnie z powstałej macierzy utworzymy macierz przestawioną (transponowaną), to otrzymaną macierz nazywamy macierzą dołączoną. Krócej: macierz dołączona jest to przestawiona macierz dopełnień algebraicznych. Macierz dołączoną oznaczamy symbolem A°, tzn.

Macierzą odwrotną A ¹ macierzy kwadratowej A nazywamy macierz, która spełnia równości

(9-7.10)

AA =1, A A = I,

* oznacza macierz jednostkową odpowiedniego wymiaru. _s ^aga. Jak wiemy, odwrotnością różnej od zera liczby a nazywamy liczbę 1 /a=a~^l; ^nia ona warunek a-a~¹ = 1. Widzimy, że macierz odwrotna spełnia podobną rolę. Ustępujące twierdzenie podaje warunek wystarczający istnienia macierzy odwrotnej:

d₀ ^macierz kwadratowa A=[a_iJfe] jest macierzą nieosobliwą, tzn. det A/0, to istnieje dokładnie jedna macierz odwrotna A^-1, która jest równa macierzy dołączonej po-