083

164 IX. Macierze, wyznaczniki, równania liniowe

Obliczamy wartość jednego z minorów macierzy W, np. utworzonego z trzech piepy, szych wierszy; mamy

164 IX. Macierze, wyznaczniki, równania liniowe

5	3	-1		5	3 2
2	1	-1	=	2	1 0
3	-2	2		3	1 K> O

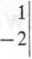
= 2-( —4 —3)= -14/0.

Zatem r(W) = 3, a tym samym r(U) = 3, więc układ jest rozwiązalny. Pomijamy więc róu. nanie nie objęte obliczonym minorem, tzn. czwarte i rozwiązujemy równoważny układ trzech pierwszych równań układu pierwotnego:

5x+3y- z = 3 ,

2x + y- z = 1,

3x-2y+2z = -4.

Ponieważ wyznacznik utworzony ze współczynników ma wartość —14 różną od zera, więc układ ten, a więc i układ pierwotny, ma jedno rozwiązanie, które znajdujemy, stosując wzory Cramera. Otrzymujemy

X ——3    v = — Z ——*“

a— ₇ ,    y ₇ , z. ₇ .

Geometrycznie oznacza to, że cztery płaszczyzny dane równaniami pierwotnego układu przecinają się w punkcie (—f,

Zadanie 9.14. Rozwiązać układ równań

4x— y= 7,

(1)    3x+ y = 14,

2x + 3y= 0.

l':

Rozwiązanie. Wypiszmy macierze współczynników W i macierz uzupełnioną

	'4 -r		'4 -1 7"
w=	3 1	, u=	3 1 14
	2 3		2 3 0

W tym przypadku rząd macierzy współczynników W może być co najwyżej równy 2 (bo nego wyznacznika stopnia wyższego niż 2 nie możemy utworzyć), gdy tymczasem . macierzy U może być co najwyżej równy 3. Ustalmy więc jej rząd. Rozwińmy w tym wyznacznik według elementów trzeciego wiersza:

	4	-1	7
det U=	3	1	14
	2	3	0

=(-l)³

-1 7 1 14

3 + 2

+(-l)    -3

4 7 3 14

= —42—105 7*0-

■

^ więc r(U) = 3, a ponieważ r(W)<3, więc warunek rozwiązałności układu nie jest speł-^ony,tzn. c^ad (1) nie ma rozwiązań (jest sprzeczny).

Geometrycznie oznacza to, że trzy proste dane równaniami (1) nie mają wspólnego unktu (w tym przypadku przecinają się parami).

§ 9.7. MACIERZE

Definicję macierzy podaliśmy w § 9.1. Dwie macierze A =[«,*], B = [ń_it] tego samego wymiaru (typu) nxm nazywamy równymi, jeśli wszystkie odpowiednie elementy obu macierzy położone na tych samych miejscach są równe, tzn.

a_ik=b_nj    dla i=l, 2,n, fc=l, 2,    , m..

Relacja równości macierzy jest

a)    zwrotna, tzn. A=A.

b)    symetryczna, tzn. jeżeli A = B, to B = A.

c) przechodnia, tzn. jeżeli A = B i B = C, to A=C.

Dwie macierze różnych wymiarów nie mogą więc być równe.

Macierzą przestawioną (lub transponowaną) nazywamy macierz, która powstaje z danej macierzy przez zamianę wierszy na kolumny, nie zmieniając ich kolejności. Macierz przestawioną względem macierzy A oznacza się symbolem A^T albo A'. Jeżeli więc A= [%],_Xm, to A^T= [ó_it]_mxn, gdzie b_ik=a_kt. Na przykład jeżeli

Macierzą zerową nazywamy dowolnego wymiaru macierz, której wszystkie elementy

H równe zeru, tzn. a_ik = 0 dla i=l, 2.....n, k=\, 2, ..., m. Macierz zerową wymiaru

^{y m} oznacza się symbolem O_nXm lub jeżeli nie prowadzi to do nieporozumień wprost -^mbolem O. Na przykład mamy

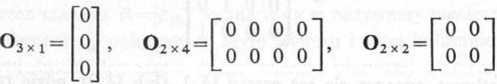
_ko|^Wśr<* macierzy prostokątnych (tzn. takich, że liczba wierszy jest różna od liczby ⁿ’ Por. § 9.1) wyróżniamy w szczególności tzw. macierz wierszową (o jednym wierszu):

Oi a₂ ... u_n]