8342937119

MAT ROFA BIN ISMAIL

luar yang harmonik dengan lembaban yang positif apabila 1x1 > 1 dan negatif apabila 1x1 < 1. Kcadaan ini dijangka menimbulkan fenomenon dwicabangan.

Levinson (1943) mcnunjukkan bahawa sistcm

(1.2) sekurang-kurangnya ada satu pcnyelesaian berkala dengan kalaan 2;r untuk semua nilai A dan jj positif. Lloyd (1972) pula membuktikan adanya penyelesaian berkala yang unik bagi sistem (1.2),

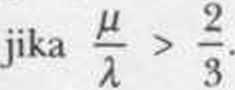
Di sini kamiakan mcnunjukkan bahawasukuan pertamasatah (/i, A) dipisahkan kepadaduarantau

olch persamaan fj = A. yang merupakan

persamaan dwicabangan bagi parameter /J dan A bagi sistem (1.2). Bilangan penyelesaian berkala dengan kalaan 2n akan berubah daripada 1 kepada 3 apabila menyeberangi

persamaan dwicabangan fJ = ——A.

«*

TATATANDA DAN TAKR1F

(2.1)    Ruang H ditakrifkan sebagai H = £ ²(0,271)

= jyl Jj*y²(r)dr < °°, y : N -» N'J

(2.2)    Subset H._2/r dari H ditakrifkan sebagai

H‘2/r ⁼{^{x e 1 x}(°) ⁼ x(2tt), x(0)=x(2/r)}; tandaan x mcnunjukkan tcrbitan x terhadap t.

(2.3)    Hasil darab terkedalam <u, v> untuk setiap u dan v di dałam H ditakrifkan sebagai

<u, v> j^utr) v(r)dr. n ^u

(2.4)    Nlisalkan A c H, A ^; mcwakili set ortogon dengan A, dan ditakrifkan sebagai

A¹ = {y g H I <y,x> = 0, Vx e A}.

(2.5)    Misalkan g(r,/i,A) sebagai suatu fungsi nyata tiga pembolehubah. Set (r,/i, A) yang memenuhi persamaan

g(r, ii_% A) = 0

dinamai set penyelesaian g. Jika b(/i, A) menunjukkan bilangan penyelesaian r bagi persamaan g = 0, dan

g(^r0> ^o’ ^ ⁼

maka titik (/i₍₎, A_Q) dirujuk tilik dwicabangan jika b(/i, A) berubah apabila (//, A) berubah dałam kejiranan (fj₍₎, A₍₎). Set semua titik

dwicabangan dikenali sebagai set dw cabangan atau persamaan dwicabangan.

IDEA DWICABANGAN PERSAMAAN VAN

DER POL

Kewujudan penyelesaian berkala persamaan Vai der Pol memang menjadi pengetahuan umun lihat misalnya Jordan dan Smith (1977) tctaf bilangan penyelesaian berkenaan masih menjad perbincangan. Guckenheimer dan Holmes (1983 memperlihatkan secaraberangkabahawa bilangaj penyelesaian tersebut bertukar daripada 1 kepacL 3 bergantung kepada nilai parameter ju dan ż Harapan kami ialah untuk menjustifikasikan hasi berangka ini melalui analisispenghampiran melalu teoremyangdikemukakan oleh Hale dan Rodrigues (1977) seperti yang dinyatakan di dałam bahagiai 3.1.* Untuk tujuan ini, kami mengikut contol prosesgangguan mencari penyelesaian berkala bag sistem tak linear daripada sistem linear seperti yang dilakukan oleh Jordan dan Smith (op.at). Hal in mungkin dilakukan berdasarkan sifat umum yang sudah dikenali iaitu sistem tak linear berkelakuar hampir serupa dengan sistem linear sęki rany sebutan tak linear kecil dan terbatasdi persekitarai tilik keseimbangan tertentu, lihat Lefschez (1977) Kaedah Jordan dan Smith tidak memberikai fenomenon dwicabangan sepenuhnya di sekita parameter (/i, A) = (0, 0) tetapi dałam bentul parameternya bersandar linear antara satu dengai yang lainnya. Untuk mengatasi masalah ini kain menggabungkan teori-teori di atas yang dibincangkan secara langsung di dałam ruang

vektor H.,^. Idea dwicabangan penyelesaian berkal. persamaan Van der Pol secara kasarnya seperi berikut:

Ruang I dipecahkan melalui pengoperasil (ditakrifkan oleh persamaan 3.1) kepada inti Ldar pelengkapnya, yakni julat L. Inti L ialah penyele saian persamaan Van der Pol dengan /i = A = 0. Inti L diberi oleh a kos (t + 0). Penyelesaian persa maan Van der Pol dengan fj, A #0 jika wujud dalan

H_2;r mestilah berbentuk hasil tambah langsung di antara inti dan julat L. Untuk menjadi penyelesat an kepada persamaan tersebut unsur tersebui mestilah memenuhi syarat dałam teorem Hale dan Rodrigues (1977). Syarat ini menerbitkan masalah dwicabangan yang diharapkan jika penyelesaian wujud.

Masalah ketaklineran persamaan Van der Po vang dipadankan dengan teorem Hale dan Ri> drigues di atas di atasi dengan mengambil /i dan > yang cukup kecil sehingga faktor ini didominankar

70

PERTANIKA VOL. 14 NO. 1.1991