117827953

To polecenie solve przyjmuje następującą postać: solve(rowl , row2, row3), inaczej mówiąc poszczególne równania rozdzielamy przecinkiem. Podobnie jak pojedynczym równaniu jeśli postać układu jest następująca:

/i(x) = qi (x) hi^x) = 92 (x)

/„(x) = 9₃(x)

To poszczególne równania rozdzielone przecinkami dodatkowo obejmujemy cudzysłowami.

2.7 Zadania

1. Wyznaczyć za pomocą Matlaba (nie liczyć na kartce!) wartości następujących granic:

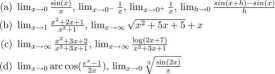
2. Obliczyć pochodne poniższych funkcji:

(a)    f(x) = 2x^{1 2} + x² — 5, f(x) = ax^{3 4 5} + 3x³ — c

(b)    f(x) = sin(x), f(x) = log_ax, /(x) = e*

(c)    f(x) =    /(x) = _Ifj, f(x) = ^

3. Rozwiązać następujące równania bądź układy:

(a)    ax — b = 0, x² — 2x + 5 = 0, x² — x + 1 = 0, ax³ + bx² + cx + d

(b)    cos(2x) + sin(x) = 1, p cos(x) = r, sin(2x) = r, sin(2x) = 1

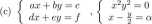
14

1

   W jakim przypadku funkcja Matlab’a taylor istotnie generuje szereg Taylor’a, a w jakim MacLaurina?

2

   Wyznaczyć szeregi Taylora (5 i 10 elementów szeregu) następujących funkcji:

(a) f(x) = sin(x), /(x) = cos(x), /(x) = lnx, f(x) = e^x, f(x) = -jf—

3

   Wyznaczyć szeregi Taylora, przyjmując że Xo = 1 i n = 3, dla następujących funkcji:

(a) f(x) = e^x, f{x) = e~^x, f(x) = lnx

4

   Za pomocą polecenia taylortool zbadać jak rząd rozwinięcia szeregu wpływa na jakość odwzorowania następujących funkcji:

(a)    /(x) = x cos(x)

(b)    /(x) = e^x, dla jakiej wartości n otrzymujemy na przedziale —27T < x < 2ir, „rozsądne” przybliżenie

5

   Przygotować wykres bez użycia narzędzia taylortool funkcję f(x) = e^xSln(^x) oraz odpowiadający jej szereg Taylora dla parametrów:

(a)    n = 5, x₀ = 2

(b)    n = 10, xo = 2

(c)    n = 15, xq = 2