1257951390

22

zatem ustalić na podstawie kryteriów mechaniki pękania omawianych w punkcie 3.3.

3.2.1. Kryteria naprężeniowe

Do opisu zniszczenia ciągliwego zazwyczaj wykorzystuje się kryterium Hof-fa, który założył warunek nieściśliwości oraz nieskończoną wartość odkształcenia w chwili zniszczenia. W przypadku jednoosiowo rozciąganego pręta o wymiarach 1 (długość), A (przekrój) wykorzystując prawo Nortona (2.3) opisujące proces pełzania oraz warunek nieściśliwości i logarytmiczną miarę odkształceń otrzymujemy następujące wyrażenia do obliczenia czasu zniszczenia ciągliwego [130]:

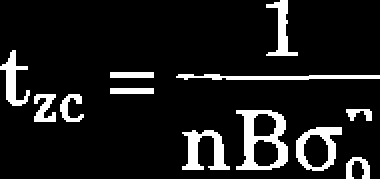
(3.5a)

Po uwzględnieniu w obliczeniach odkształcenia sprężystego, czas zniszczenia ciągliwego określa zależność:

t -

nBoJ

n o₀ _ n - 1 E n

(3.5b)

gdzie: a₀ - naprężenie w pręcie.

W analizie zniszczenia kruchego wykorzystuje się wprowadzony przez Ka-czanowa parametr ciągłości \|/ lub też parametr uszkodzenia w (co = 1 - \|/). W chwili początkowej co = 0, w momencie zniszczenia co = 1. Równanie opisujące propagację parametru uszkodzenia ma postać [88]:

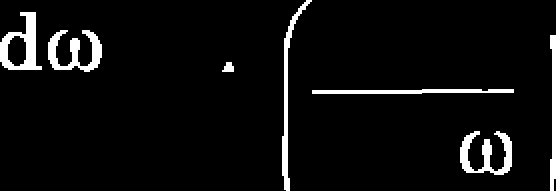
(3.6)

gdzie: A, m - stałe materiałowe.

Dla stałego jednoosiowego naprężenia Gi otrzymujemy po scałkowaniu zależności (3.6) następujące wyrażenie na czas zniszczenia kruchego

A(1 + m) of

(3.7)

W przypadku działania zmiennego naprężenia a₀(t) całkując wyrażenie (3.6) mamy:

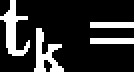
A(1 + m)(a₀(t))^m

(3.8)

Ostatnia zależność jest znaną zasadą ułamków trwałości Robinsona.

W przypadku wystąpienia zniszczenia typu mieszanego obowiązują założenia dotyczące zarówno zniszczenia ciągliwego, jak i kruchego. Wówczas dla jednosiowego pręta czas zniszczenia możemy obliczyć z zależności:

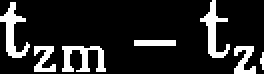
n - m t_zk n

(3.10)

która jest słuszna dla t_zm < t_2C.

Zastosowanie wymienionych kryteriów w odniesieniu do złożonych elementów oraz złożonych stanów naprężeń wymaga stosowania odpowiednio zmodyfikowanych równań konstytutywnych. Zagadnienie to zostanie omówione w pkt. 5.

3.2.2. Kryteria odkształceniowe

Wyniki badań prowadzonych przez wielu badaczy omówione m.in. w pracy [100] wskazują, że brak jest bezpośredniej korelacji pomiędzy czasem zniszczenia a odkształceniem całkowitym w chwili zniszczenia.

Jednocześnie Monkman i Grant stwierdzili poprawność następującej formuły [111]:

^£min tz = const    (3.11)

mówiącej, że iloczyn minimalnej prędkości pełzania w stanie ustalonym i czasu zniszczenia pozostaje stały. Zależność ta umożliwia obliczenie czasu zniszczenia próbki przy znajomości wyników przyśpieszonego testu na pełzanie w wysokiej temperaturze. Uogólnieniem tej zależności jest formuła

(3.12)

^£min COnst