1257951401

44

rych funkcja ta przyjmuje wartości ujemne, a przez 1 całkowitą liczbę symulacji, prawdopodobieństwo zniszczenia obliczymy jako:

Pf = y    (4-57)

Dokładność powyższego oszacowania rośnie ze wzrostem liczby symulacji 1. Generalnie wymagana liczba symulacji powinna wynosić co najmniej 10/Min(p_f), gdzie Min(p_f) oznacza minimalną wartość prawdopodobieństwa zniszczenia uzyskaną w obliczeniach [38].

4.5.2. Metoda estymacji punktowej (PEM)

Metoda estymacji punktowej pozwala obliczać pierwsze 2 momenty, tzn. wartość oczekiwaną i odchylenie standardowe opierając się na stosunkowo niewielkiej liczbie symulacji [106, 139].

W przypadku funkcji Y jednej zmiennej losowej X o wartości oczekiwanej |i_x i wariancji s_x wyrażenie na moment zwyczajny rzędu k zmiennej Y ma postać:

(4.58)

E(Y^k) = P₊ y* + P_

gdzie: P₊ = P_ =    y₊ = Y(^_x + s_x),    y_ = Y(^_x - s_x)

A zatem wartość oczekiwaną nowej zmiennej losowej Py oraz jej wariancje s_y obliczymy jako:

(4.59)

Hy = E(Y) = - (y₊ + y_)

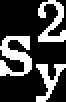
y+-y-

(4.60)

Dla nie skorelowanych m zmiennych losowych wyrażenie (4.58) ma postać:

^E(^Yk)=^ (y^+■ ■ ■+y^)    w-od

gdzie: y odpowiada wartości funkcji Y określonej dla wartości argumentów

hxi + s_xi, p_x2 + s^,-.. natomiast y_oznacza wartość funkcji Y w punkcie

hxi " Sxi> Px2 ^- Sx2,. - - dla wszystkich m zmiennych losowego wektora X.