1257951431

98

Na podstawie zależności (7.37) i (7.38) można stworzyć diagram (rys. 7.4) o

osiach — £f oraz C obejmujący wyniki badań doświadczalnych. Granice tego

obszaru wyznaczone są przez krzywe propagacji w płaskim stanie naprężenia (psn) i płaskim stanie odkształcenia (pso). Zależność podana na rys. 7.4 jest niezależna od rodzaju materiału.

Przy braku informacji o wartości odkształcenia pełzania przy zniszczeniu, prędkość propagacji można oszacować na podstawie następujących formuł wiążących tempo propagacji ze współczynnikiem intensywności naprężeń K, naprężeniami bazowymi Gr oraz czasem zniszczenia t_z(R_} przy naprężeniu Gr [135]:

— dla płaskiego stanu naprężenia

da

dt

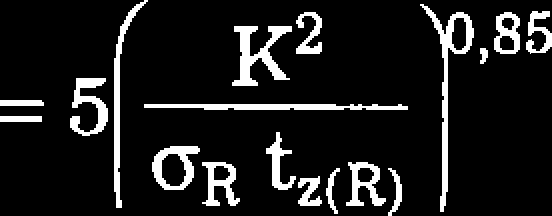
(7 39)

C* (MJ/m² h)

Rys. 7.4. Diagram do oceny propagacji pęknięć w warunkach pełzania Fig. 7.4. Creep crack growth assessment diagram

(7.40)

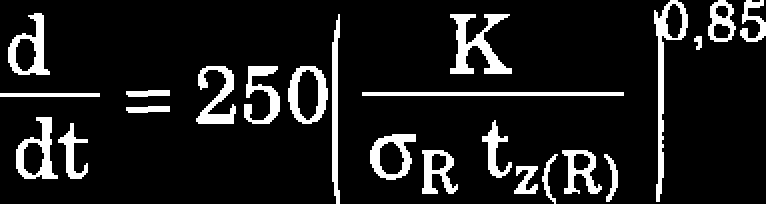
Podane powyżej formuły są przybliżonymi zależnościami pozwalającymi dla celów praktycznych obliczać tempo propagowania pęknięcia. Dokładniejsze rezultaty można osiągnąć wyznaczając parametry równania (7.34) na podstawie badań doświadczalnych przeprowadzonych na próbkach z danego materiału.

Jeżeli rozwój pęknięcia następuje w obszarze, w którym równocześnie zachodzą intensywne pełzaniowe procesy degradacyjne charakteryzowane parametrem zniszczenia co, to tempo propagacji może opisywać zmodyfikowana zależność [96, 135]

(7.41)

- dla płaskiego stanu odkształcenia

da_ DoC*⁹ dt 1 - co

Równanie powyższe należy uzupełnić zależnością opisującą tempo wzrostu parametru zniszczenia co.

7.2.3. Propagacja pęknięć w warunkach obciążeń cyklicznych

W warunkach obciążeń cyklicznych wywołanych rozruchami lub zmianą mocy turbiny propagację pęknięć opisuje równanie Parisa lub jego modyfikacje [45, 71, 81]

H o

dN

= AAK^<P

N

(7.42)

gdzie:

A, (p — stałe,

AK — zakres zmian współczynnika intensywności naprężeń.

Całkowity przyrost pęknięcia w danym cyklu pracy możemy obliczyć jako sumę przyrostów wywołanych obciążeniem cyklicznym oraz przyrostów powodowanych pełzaniem materiału

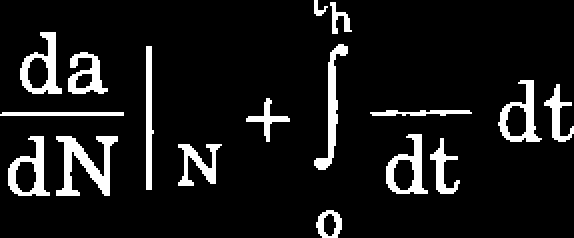
(7.43)

gdzie: t^ jest czasem pracy ustalonej w danym cyklu.