1629290284

Journal of Aeronautica Integra

1/2006 (1)

PT

UJĘCIE BILANSOWE I WARIACYJNE BELKI BERNOULLIEGO-EULERA JAKO MODELU LOTNICZYCH ELEMENTÓW KONSTRUKCYJNYCH

Krzysztof Arczewski, Józef Pietrucha

1.    WSTĘP

Belka jest modelem fizycznym wielu elementów konstrukcji lotniczych, np. skrzydła, łopat śmigłowca, czy łopatek turbin gazowych i dlatego znajomość modelu matematycznego drgań belki jest istotnym fragmentem wykształcenia w zakresie specjalności lotniczych. Belka jest więc obiektem ważnym, a zarazem prostym, dla którego można (bez nadmiernego wysiłku) zaprezentować dwie podstawowe metody tworzenia modeli matematycznych, tj. bilansową i wariacyjną. Tworzenie modelu matematycznego belki jest zarazem dobrą okazją do zaprezentowania podstaw metodyki racjonalnego modelowania układów technicznych (zob. [1]).

2.    DWIE METODY TWORZENIA PRZYCZYNOWYCH MODELI MATEMATYCZNYCH ZJAWISK FIZYCZNYCH

W licznych publikacjach dotyczących dynamiki układów ich ważną częścią jest model matematyczny zjawiska. Bywa tak, że jest on z góry postulowany i dalej analizowany, bywa też tak, że jest on tworzony na podstawie wcześniej sformułowanych przesłanek, w tym przede wszystkim przyjętego modelu fizycznego. Wśród publikacji tego drugiego rodzaju spotkać można prace, w których model matematyczny jest rezultatem racjonalnego, uporządkowanego procesu, są wszakże prace wskazujące na brak metodyki tworzenia modelu, w których model wydaje się dziełem przypadku, a nierzadko bywa nawet błędny.

Cel niniejszej publikacji jest zatem wyłącznie dydaktyczny - chodzi o wskazanie racjonalnego podejścia i przedstawienie metodyki modelowania na przykładzie belki, mogącej wykonywać drgania.

Istnieją dwie podstawowe metody tworzenia modeli zjawisk fizycznych makroskopowych (w naszych rozważaniach pomijamy procesy z mikroświata). Jedna to metoda bilansowa, u podstaw której znajdują się bilanse wielkości ekstensywnych. W mechanice jest to bilans masy, pędu, krętu, a w razie konieczności także energii.

Druga z metod - wariacyjna - polega na bezpośrednim zastosowaniu zasad wariacyjnych, zwłaszcza zasady Hamiltona.

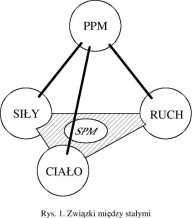
Dla wyjaśnienia metody bilansowej posłużymy się schematem przedstawionym na rys. 1, który umownie będziemy nazywać piramidką modelarską W piramidce głównym wyróżnikiem są Podstawowe Prawa Mechaniki (PPM), które mogą być wykorzystywane w tworzeniu modelu dowolnego zjawiska dynamicznego. W podstawie piramidki znajdują się Szczegółowe Prawa Mechaniki (SPM), znane także pod nazwą prawa konstytutywne, specyfikujące rodzaj ciała biorącego udział w zjawisku, którego model tworzymy. W dolnych wierzchołkach piramidki występują zbiory, do których odwołujemy się w procesie modelowania. Na przykład w zbiorze Ruch tkwią m.in. związki między przemieszczeniami a odkształceniami, zaś w zbiorze Ciało tkwią związki między stałymi charakteryzującymi materiał, np. modułem Youn-ga E i liczbą Poissona v a stałymi Lamćgo dla materiałów izotropowych.

charakteryzującymi materia!

3