1650025962

Jednowymiarowy stan naprężenia

Przez każdy punkt pręta rozciąganego można przeprowadzić nieskończona liczbę przekrojów pod różnymi kątami do jego osi i każdemu przekrojowi będzie odpowiadało inne naprężenie.

Rozpatrywany jest pręt pryzmatyczny rozciągany siłami osiowymi P.

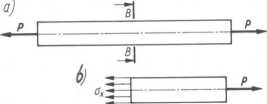
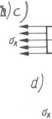
W przekroju B-B, prostopadłym do osi pręta, naprężenia normalne rozkładają się równomiernie

(26)

P

°^x ~ A

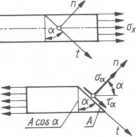
Do dalszej analizy wycina się, myślowo, element pręta dwoma równoległymi do siebie przekrojami, prostopadłymi do osi pręta. W obu tych przekrojach występują naprężenia normalne a_x, rozłożone równomiernie w tych przekrojach, element ten jest następnie przecinany płaszczyzną przechodzącą pod kątem a do przekroju poprzecznego.

Taki sam kąt a będzie tworzyła normalna n do przeciętego przekroju z osią pręta. Aby odcięta część elementu pręta pozostawała nadal w równowadze to naprężenia normalne a_a i styczne x_a działające w tym przekroju muszą zrównoważyć naprężenia a*.

Warunki równowagi, z rzutu siła na osie n - normalną i t - styczną wynoszą:

/ P_n = a_aA — a_xA cos a cos a = 0

(27)

P_t = t„A — a_rA cos a sin a = 0

stąd

a„ = a_xAcos²a

T_a = a_x sin a cos a — 0,5a_x sin 2a (28)

jak widać to wielkości tych naprężeń zależą od kąta a naprężenia normalne (maleją ze zwiększaniem kąta a)