1935182603

14

SPIS TREŚCI

Definicja 0.3.3 (Ciąg ograniczony) Niech będzie dany ciąg liczbowy (a_n)_nem> to powiemy że jest on

ograniczony z góry: gdy (3M G R)(Vn G N)    < M,

ograniczony z dołu: gdy (3m G R)(Vn G N) m < a_n,

ograniczony: gdy jednocześnie jest ograniczony z góry i jest ograniczony z dołu.

Oczywiście mamy następujący fakt

Fakt 0.3.1 Ciąg liczbowy (on)neN jest ograniczony wtedy i tylko wtedy gdy

(3M G R)(Vn G N) |o„| < M.

Przykład 0.3.3 Rozważmy dwa ciągi (a_n)_n6N,

•    jeżeli dla dowolnego n G N a_n = ^y, to wtedy 0 < ^y < 1, więc (a_n)neN jest ograniczony,

•    jeżeli dla dowolnego n G N b_n = n², to wtedy dla każdego n G N mamy 0 < b_n i dla dowolnej liczby rzeczywistej M G R istnieje no G N takie że M < % ale mamy również n < n² dla każdej liczby naturalnej n. Więc ostatecznie dla każdej Mg R istnieje no G N takie że M < n% = b„₀. Reasumując, (b_n)_n€n jest ciągiem ograniczonym z dołu ale nie jest ciągiem ograniczonym z góry.

Twierdzenie 0.3.3 (Weierstrassa) Każdy ciąg ograniczony zawiera podciąg zbieżny.

Dowod. Załóżmy, że ciąd (a„)neN jest oganiczony, weźmy pod uwagę następujący zbiór:

P=|iGR: |{n G N : a_n < z}| < N₀

Zauważmy, że nasz zbiór jest niepusty i nie jest całą prostą R, co wynika z tego, że istnieje takie m, M G R, że m < a_n < M dla dowowlnego n G N (ciąg ograniczony). Niech x G P i y < x, to wtedy prawdziwa jest inkluzja

{n G N : a_n < y} C {n G N : a_n < x}

ale ten większy zbiór jest skończony, więc {n G N : a_n < y} jest skończony a stąd y G P, więc P jest przedziałem ograniczonym z góry. Stąd istnieje kres górny g G R zbioru P. Niech k G N to {n (żN : On < g — £} jest skończony oraz {nGN:a„<j + |} jest nieskończony, więc

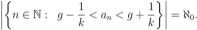
Więc istnieje mk > k, że a_mk G (ff —    + f), ale k € N jest dowolne, co kończy dowód naszego

twierdzenia. ■

Zachodzi w pewnym sensie twierdzenie odwrotne do poprzedniego.