3179027801

Elementy Badań Operacyjnych

nego możliwie najbliżej początku układu współrzędnych). Jak widać F(xx₂) = 30x_t + 20x₂ = 6000 można przesunąć równolegle tak, że będzie ona styczna do zbioru rozwiązań dopuszczalnych w punkcie D o współrzędnych:

Xi* = 200; x₂* = 600; F(x,*, x₂*) = 30 • 200 + 20 • 600 = 18000.

Zatem należy produkować 200 sztuk wyrobu Wi i 600 sztuk wyroby W₂, co da przychód ze sprzedaży (maksymalny przy istniejących ograniczeniach) w wysokości 18000 zł.

Ad b) Jeżeli cena wyrobu Wi zostanie podwyższona do 40 zł, zbiór rozwiązań dopuszczalnych nie ulegnie zmianie, może natomiast zmienić się rozwiązanie optymalne, bo zmienia się kąt nachylenia (współczynnik kierunkowy) funkcji celu. Nowa funkcja kryterium przyjmuje postać: F’(x\, x₂) = 40xi +20x₂, a po przyjęciu jej początkowej wartości np. 8000 wykres funkcji F’(xi, x₂) = 40xi + 20x₂ = 8000 zaznaczono także na rys. 1.2.

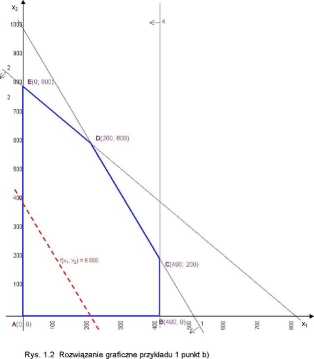
Przesuwamy ją następnie w górę szukając punktu należącego do wieloboku ABCDE położonego możliwie najdalej od początku układu. Jak widać najwyższe jej położenie pokrywa się z odcinkiem CD zbioru rozwiązań dopuszczalnych [nietrudno zauważyć, iż funkcja F’(xi, x₂) jest równoległa do prostej (1), do której należy odcinek DE, tzn. ich współczynniki są odpowiednio proporcjonalne], zatem cały odcinek CD będzie obecnie zbiorem rozwiązań dopuszczalnych. Jak łatwo sprawdzić, wartość funkcji celu w obu punktach jest taka sama: F’(C)=40-400 + 20-200 = 20000 i F’(D) = 40-200 + 20-600 = 20000. Taką samą wartość przyjmie funkcja celu w dowolnym innym punkcie odcinka CD. W tym przypadku mamy nieskończenie wiele rozwiązań optymalnych, dwa przykładowe to:

Antoni Goryl, Anna Walkosz: Programowanie liniowe strona 9