4189283847

48 Konrad Eckes

W opisie modeli będzie stosowany następujący schemat charakteryzujący zapis obiektów i relacji:

O zapis geometrii elementów strukturalnych,

O zapis topologii (jeżeli w danym modelu relacje topologiczne są stosowane),

O zapis obiektów rzeczywistości geograficznej.

Model obiektowy nietopologiczny

Model obiektowy nietopologiczny nazywany jest także w literaturze prostym modelem wektorowym (Gaździcki, 1990). W zapisie tym obiekty punktowe nie wymagają dalszej redukcji, natomiast obiekty liniowe i powierzchniowe podlegają rozwinięciu do postaci list liniowych. Pełny zapis w tym modelu składa się z katalogu współrzędnych punktów (tab.l), powiązań punktów w wektory (tab.2) oraz trzech plików z zapisem obiektów punktowych, liniowych i powierzchniowych. Oznaczenia do zapisów zostały przedstawione na rysunku 3.

Tabela 1. Katalog współrzędnych punktów    Tabela 2. Plik powiązania punktów w wektory

Oznaczenie wektora	Punkt początkowy	Punkt końcowy
^V3-4	3	4
^V4-5	4	5
^V20-2I	20	21

Numer punktu	X	Y
1	x,	y,
2		y2
21	^X2,	y2i

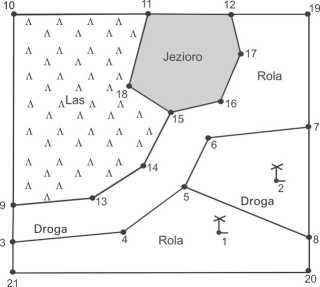
Rys. 3. Wycinek mapy zawierającej trzy grupy obiektów, z oznaczeniami - do zapisu obrazu obiektów w modelu obiektowym nietopologicznym

Zapis obiektów punktowych składa się z oznaczenia obiektu oraz określenia miejsca położenia za pomocą współrzędnych (tab. 3). Zapis obiektów liniowych polega na zestawieniu kompletnej listy wektorów, które ten obiekt tworzą (tab. 4).

W podobny sposób zapisywane są obiekty powierzchniowe, przy czym w tym przypadku zestawiana jest lista wektorów granicznych obiektów (tab. 5).

Przedstawiony tutaj zapis, zawierający wektory, został zastosowany celowo - dla podkreślenia faktu, że w tym modelu wektory stanowią jednostki strukturalne obiek-