5167288051

Analiza rozkładu pola temperatury w tkance nowotworowej _w RF hipertermii

Eugeniusz KURGAN, Piotr GAS

Akademia Górniczo-Hutnicza, Katedra Elektrotechniki i Elektroenergetyki

Czas przeżywalności pacjentów z różnymi rodzajami guzów nowotworowych nie jest duży między innymi dlatego, że występują częste nawroty. Hipertermia w zakresie fal o częstotliwościach radiowych poniżej 100MHz noże być pomocna, jako uzupełnienie tradycyjnej radio- i chemioterapii. Dotyczy to głównie tkanek nowotworowych położonych dostatecznie blisko powierzchni ciała, ponieważ przenikanie pola w głębsze warstwy ciała jest utrudnione z powodu indukowania się prądów wirowych oraz strat dielektrycznych. Przeprowadzone badania kliniczne wskazują, że hipertermia może być efektywnym narzędziem zapobiegającym rozrastaniu się guza.

Stosowanie hipertermii polega an ogrzewaniu tkanki nowotworowej do temperatury większej niż 42°C nie powodując przy tym przekroczenia normalnej fizjologicznej temperatury tkanek sąsiednich, która jest niższa niż 42°C. Zakres temperatury, jaką mamy tu do dyspozycji jest zwykle bardzo mały. Jeśli temperatura guza jest niższa niż 42°C, działanie terapeutyczne praktycznie nie występuje, jeśli natomiast temperatura jest większa od 44°C, wtedy tak tkanka zdrowa, jak i chora są uszkadzane. Zwykle średnica naczyń krwionośnych w tkance nowotworowej jest większa niż w otaczających tkankach i dlatego temperatura guza jest podczas hipertermii też większa od temperatury otoczenia. Jest to spowodowany przede wszystkim większą przewodnością krwi, niż komórek nowotworowych.

W analizie rozkładu temperatury mamy do czynienia z polem sprzężonym elektromagnetycznym i temperatury. Pola te są opisane następującymi równaniami:

V x H = J_s + J_c + jco D ^

gdzie J_s jest niezależnym prądem wymuszającym a J_c prądem przewodzenia. Po wprowadzeniu potencjału magnetycznego B = V x A oraz przy założeniu, że J_c = o E, D = e E oraz VxE = —jcoB, otrzymujemy:

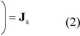
{-OS + j<j)co\ + Vx|— Vx A

Pole magnetyczne jest sprzężone z polem temperatury poprzez równanie Pennesa:

V(~kVT) = p_bC_b0)_b(T„ -T)+Q„ + Q_ma (3)

gdzie Qexi = a E² jest wydzielającym się w wyniku indukcji w ciele, Q_met jest ciepłem metabolizmu ciała ludzkiego, co* jest współczynnikiem przepływu krwi, C* ciepłem właściwym krwi, k jest współczynnikiem przewodności cieplej tkanki.

17