5282745665

Staty styczna ocena wyników pomiam do analizy błędów i oceny niepewności otrzymywanych wyników wykorzystuje się modele i metody rachunku prawdopodobieństwa i statystyki matematycznej.

Przeprowadzenie serii pomiarów- czyli n-krotne powtórzenie pomiaru tej samej wielkości , daje szansę na wyznaczenie błędów o charakterze przypadkowym i nadmiernym. Zmiana metody pomiaru pozwala na zauważenie błędu systematycznego. Sposób doboru metod pomiarowych i powtórzenia pomiaru musi być wybrany świadomie, dając szansę na wykrycie błędów jednej z wymienionych kategorii.

Błędy systematyczne w pomiarach tej samej wartości pewnej wielkości , w niezmiennych warunkach, tym samym narzędziem i metodą pomiarową, przeprowadzonych przez tego samego obserwatora pozostają stałe. Wykrycie tych błędów jest możliwe przez powtórzenie pomiarów po zmianie jednego z czynników wpływających na wynik, np. innym narzędziem, w innej temperaturze, w innym miejscu, w przypadku pomiarów pośrednich przez skorzystanie z innej zależności funkcyjnej między wynikiem a wielkościami mierzonymi bezpośrednio. ( w ćwiczeniu wyniki pomiaru pola trójkąta można okręcić z różnych wzorów i- z długości podstawy i wysokości lub tylko długości boków trójkątajtp.

Błąd przypadkowy powoduje , że wyniki kolejnych pomiarów zmieniają się w sposób losowy, mimo, że mierzona jest ta sama wartość wielkości w warunkach praktycznie niezmiennych. Wynikami pomiarów obarczonymi błędami przypadkowymi rządzą prawa statystyki i ich modelem matematycznym jest rozkład normalny (Gaussa).

Błędy nadmierne (grube, omyłki) powodują wyraźne odstępstwo wyniku pomiaru w serii od pozostałych wyników otrzymanych w praktycznie niezmiennych warunkach. Bardzo często ich bezpośrednim źródłem jest wykonujący pomiary człowiek.

Opracowanie serii wyników pomiarów Xj ( dla i = 1,2......n ) i wnioskowanie o ich

niepewności rozpoczyna się od wyznaczenia podstawowych parametrów statystycznych danej serii n-elementowej:

wartości średniej arytmetycznej z n pomiarów:

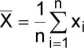
- odchylenia standardowego ( odchylenia średniokwadratowego ) wyników pomiarów od wartości średniej:

Zfx_i-Xj²

s

n-1

Różnica miedzy wartością średnią z wyników pomiarów i wartością, którą można uznać za poprawną wyznacza błąd systematyczny popełniany w każdym z pomiarów w serii.

Modelem matematycznym błędów przypadkowych jest rozkład normalny (Gaussa) opisany funkcją rozkładu gęstości prawdopodobieństwa f(x) zdarzeń losowych, którymi są kolejne wyniki pomiarów x :

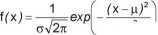
2c^: