604000759

podczas badań laboratoryjnych. Model matematyczny opisany równaniem (5.3) [102] posiada dwa elementy składowe. Pierwsza część (równanie 6.1) jest iloczynem funkcji krzywej sigmoidalnej i funkcji ekwipotencjalnej, która opisuje obwiednię sygnału EA, formując kształt jej czoła i wygaszenie. Druga część (równanie 6.2) opisuje periodyczność sygnału EA przy pomocy sumy harmonicznych kosinusoidalnych, kształtując w ten sposób wypadkową częstotliwość.

ysECO =

l+e~^A2(^c~Pi)

A₃(.t H2) | Część pierwsza.

(5.1)

(5.2)

(5.3)

y_sc(t) = cos(2nfit) } Część druga,

i

¹    _e—i4₃(t—#ł₂) ^ A_cosicos (2nft),

gdzie: y(t) - sygnał EA generowany przez WNZ, A/ - amplituda funkcji sigmoidalnej [—], A2 - współczynnik skali funkcji sigmoidalnej, Aj - współczynnik skali funkcji ekspotencjalnej, Pi~ współczynniki lokalizacji funkcji sigmoidalnej, ^-współczynniki lokalizacji funkcji ekspotencjalnej, Acost-współczynniki amplitudy kolejnych i-tych funkcji kosinusoidalnych, /- częstotliwość kolejnych i-tych funkcji kosinusoidalnych, / 6 {10,20,30,... 600} kHz, k - liczba harmonicznych tworzących sygnał, dla modeli symulacyjnych przyjmowana była wartość k = 60, t - zmienna niezależna, czas [s] [102],

Zjawisko WNZ ma charakter wieloźródłowy [56, 104]. Matematyczny opis wieloźródłowości sygnału EA uzyskano za pomocą złożenia ^-pojedynczych sygnałów (opisanych równaniem 5.2), definiując dla każdego z nich inne wartości częstotliwości, fazy i amplitudy. Ze względu na falowy charakter sygnałów EA generowanych przez WNZ zastosowano zasadę superpozycji, sumując wartości amplitud dla dyskretnych wartości czasowych [55, 104, 105],

Do zamodelowania sygnału wykorzystano kilkadziesiąt sygnałów (tzn. parametr k = 60) o różnej wartości parametrów, estymując takie wielkości jak: częstotliwość i amplituda przy zastosowaniu opracowanego przez autora oprogramowania.

a)

b)

■ lilii

I-

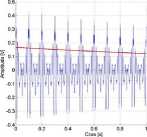
Rys. 5.4 Przebiegi czasowe sygnału EA generowanych przez WNZ zarejestrow'ane podczas pomiarów' laboratoryjnych a), modelu matematycznego z estymowanymi parametrami b), opracowanie własne.