7270841593

17. Właściwości liniowości i stacjonarności systemów.

Opracowano na podstawi wykładu 3 i 4 z SD, materiału z ćwiczeń z PA,

Liniowość systemów:

Mówimy, że system jest liniowy jeżeli spełnia on zasadę superpozycji, to znaczy, że posiada on następujące właściwości:

• Jednorodność: Wyjście systemu pobudzanego pojedynczym wejściem u(t) wzmocnionym w stopniu jest wzmocnionym w takim samym stopniu wyjściem systemu odpowiadającym wejściu u(t).

v(t) - 0(a»(/)) = aO(u(t))

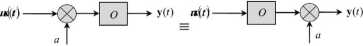
• Addytywność: Wyjście systemu pobudzanego przez sumę wejść jest taką samą sumą jego wyjść obserwowanych dla każdego z tych wejść oddzielnie.

<¥W

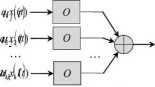
y(t)--Ollu,(t) = •| o |—* y(0 =

Łącznie zasada superpozycji: Jeśli wejście Xi(t) daje wyjście yi(t) i wyjście x₂(t) daje wyjście y2(t), to wejście aiXi(t)+a₂x₂(t) daje wyjście aiyi(t) + a₂y2(t)

•    Liniowość badamy w warunkach początkowych

•    Układ liniowy musi być taki dla dowolnych sygnałów wejściowych.

Na nieliniowość wskazują:

•    jakiekolwiek niezerowe stałe w opisie systemu,

•    jakiekolwiek nieliniowe wyrażenia związane z sygnałami takie np. jak x²(t) , x(t)y(t) i pochodnymi sygnałów ciągłych czasu w równaniu różniczkowym lub różnicowym

Inne właściwości liniowości:

•    system opisany jest tylko równaniami liniowymi

•    nie ma żadnych ograniczeń zmiennych.

Stacjonarność systemów

Mówimy, że system jest stacjonarny, jeżeli dowolne przesunięcie czasu 0 dla sygnału wejścia u(t+0) powoduje takie samo przesunięcie czasu dla sygnału wyjścia, to znaczy:

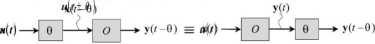
przy założeniu, że wyjście dla wejścia u(t) wynosi y(t) i warunki początkowe są identyczne.

Na niestacjonarność wskazują:

•    jakiekolwiek niejednostkowe stałe związane z argumentem czasu np. u(2t), u(-t), u[2n], u[-n]

•    jakiekolwiek współczynniki będące funkcjami czasu w równaniu różniczkowym lub różnicowym

Stacjonarne

Przykłady —*    >    ,

po lewej ciągłe    —ylA -    v[«l = — (w[«- l] + ll[n\ t w[«+ ii)

po prawej stacjonarne    dt    3    ⁷

Niestacjonarne

4-y(t)= MO-ĄM* “M    y\n\= -y\n- z]+«[«]

dt    n