7292100743

(21)

444 Miernictwo.

Długość łuku wynosi przy kącie środkowym a:

ł

P. K

r •

180°

Wytyczenie punktów głównych kontrolujemy, mierząc na p. tflcąty PS W i WSK, które powinno być równe 90°-(--a. Błędy do l^r zw. tolerujemy.

Ponieważ punkty główno nie leżą zw. na miedzach itp. i mogą być z tego rodu zniszczone, należy jo starannie ubezpieczyć, ozuaczająe poprowadzone

w nich prostopadłe do osi trasy dwoma, wzgl. czterema punktami przy równoczesnem zmierzeniu odpowiednich odległości.

- Sposoby wytyczania punktów pośrednich łuków kołowych. 1. Metoda spółrzednych prostokątnych.

a) Tyczenie od stycznej^ (patrz lig. 111).

Znając w dowolnym punkcie łuku A kierunek stycznej, obieramy go za oś a-ów, a punkt A za początek układu.

Punkty pośrednie łuku wyznaczamy, odcinając dla obranych odciętych x rzędne tj, obliczone z wzoru dokładnego:

_ Yr*~—    .............(22)

.(23)

pou

Fig. 111.

y *= >*

X

V

lub uproszczonego: y ■■    ~ -j--,

r

b) Tyczenie od cięciwy (patrz fig. 112).

przyczem y

2 r

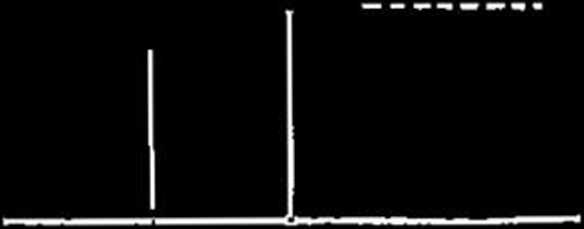
Tycząc luk od cięciwy (A — początkowy układ, kierunek cięciwy — oś

a--ów), otrzymamy ze względu, że y'    ■    -

x' —--x, związek:

u ’

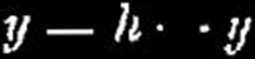
lub w przybliżeniu    y

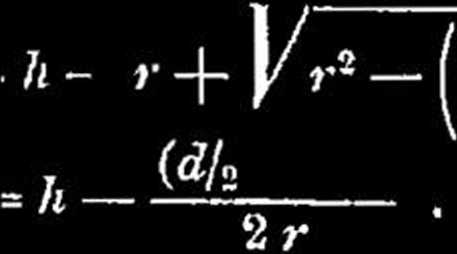
(24)

(24*)

przyczem    h — 2 r sin² - , zaś — d - - r sin «k/₂.

Tt    Łi

Metody tej można użyć przy wytyczaniu punktów głównych, o ile kąty proste będziemy tyczyli przy pomocy teodolitu; przy wytyczaniu punktów pośrednich używa się w tym celu węgieluicy pryzmatycznej.

2. Metoda biegunowa (kątów obwodowych). Równym odcinkom 7 łuku tego samego koła odpowiadają równe kąty obwodowe z>, przyczem (patrz fig. 113):