8181341963

152

PKZMłLAD TECHNICZNY

1908.

Urót .1 "Ar-vs jv,ecHANi!;i

w języku wektorów.

Przez Ludwika Silbersteina.

^Ciąg dalszy do str. 129 w Aś 10 r. b.1.

Związki kinematyczne.

Aby określić chwilowe położenie obracającej się bryły względem układu 0, t. j. względem układu „nieruchomego*, wprowadza się zazwyczaj, w wypadku ogólnym trzech stopni swobody, trzy powszechnie znano kąty Euler'a: 0, <|>, cp. Składowe prędkości obrotowej bryły p_v p_v p₃ wyrażają się wów- ^;

(46),

czas przez liniowe funkcyo pochodnych 0, »{>, <p o współczynnikach zależnych od samych 0, <]>, <p. w sposób dość prosty zresztą (por. wyżej cytowane dzieła). Związki to noszą nazwę równań kinematycznych Euler a.

Kąty Eulkka są bardzo dogodnymi parametrami, szczególniej, że jest icli trzy, a więc tyle, ile obracająca się bryła posiada stopni swobody. Wybór ich opiera się jednak na pewnem uprzywilejowaniu jednej z osi względem dwóch innych; innemi słowy, kąty 0. <p bynajmniej nie są równorzędne sobie co do znaczenia geometrycznego; dzięki tomu zaś znika sy metry a wzorów.

Przy wektorowym sposobie przedstawienia rzeczy, związki kinematyczne są już właściwie zawarte w równaniu (22), zastosowanem do dowolnego wektora w związanego nierozerwalnie z bryłą (dw^dt — 0), a więc w równaniu

• dli) _T/

W =    = Vpw .

dt *

Możemy w niem położyć za w wektor r odpowiadający dowolnemu punktowi bryły, a więc napisać

r = Vpr.

Możemy też położyć kolejno lv = JO,,    JO_:i, przy znaczeniu

symbolów powyżej objaśnionem. YVówczas otrzymamy trzy równania różniczkowe woktorowe:

JC_X = Vpj[' 1 JL\ = Vpj0₂

*•■3 = ^T> -*--₃

które możemy uważać jako wyraz związków kinematycznych. W tym układzie równań rola wszystkich trzech osi głównych jest jednakowa. Mamy tu wprawdzie trzy wektory jednostkowe, równoważne sześciu skalarom, podczas gdy bryła posiada trzy tylko stopnie swobody; innemi słowy, jc_Xy jo._iy jo_z nie stanowią zmiennych wzajemnie niezależnych, jak 0, «[», <p; lecz zato żadna z osi ruchomych nie jest uprzywilejowana.

Przypomnijmy sobie, że wektory jo_X) jc₂, JO₃ są nietyl-ko jednostkowe, lecz wzajemnie do siebie prostopadłe, tak iż oprócz

jl\² — jr₂² = jc_z² = 1, mamy jeszcze trzy warunki skalarne:

JO JO z — JO 3 mM* j —- JO j JO 2 — 0 ,

0

a więc istotnie tylko trzy wzajemnie niezależno parametry skalarne. Możemy jednak pozostawić ao_lt J0_2i JC_Z w związkach kinematycznych, pamiętając o tych warunkach skalarnych, acz nio wyzyskując ich z góry i raz na zawsze.

I

W związkach (40) prędkości JO_x i t. d. są wyrażone przez prędkość obrotową bryły p i przez same JO_x i t. d. Opierając się na tych związkach, możemy toż wyrazić natychmiast składowe p_x i t. d. wektora p wzdłuż osi ruchomych przez

prędkości JO_x etc. i przez same wektory JO_x etc. Istotnie mnożąc skalarnie ostatnie równanie (46) przez JO.,, otrzymamy:

J0₂ JC ₃ = JO., V p jo ₃ = pVjP₃J0₂] lecz    V JO2 J0₂ =— JO_x, pjo_x=p_x,

a więc:    J0₂ J0₃ = — p_v.

Różniczkując zresztą JC₂ JCj -= 0 ze względu na czas, mamy • • •

JOr, J0₃ = ' — JO■, J0₃, a więc p_x = J0₂ jv₃. Podobne dwa równania wynikają stąd przez cykliczne przestawienie wskaźników. Otrzymamy tedy żądane związki w postaci

Pi —

P i — JC\

f

p₃ = JD_X JC,

w której żadna z osi nie jest wyróżniona, czyli uprzywilejo-, wana.

• Nie chciałbym przez to powiedzieć, że jo_x, jo₂, JO_z będą : dla celów specyalnie rachunkowych również dogodne jak pa-| rametry O, '{>, cp.

I

Całka liniowa i curl wektora, ilustrowane na przykładzie

poruszającej się bryły.

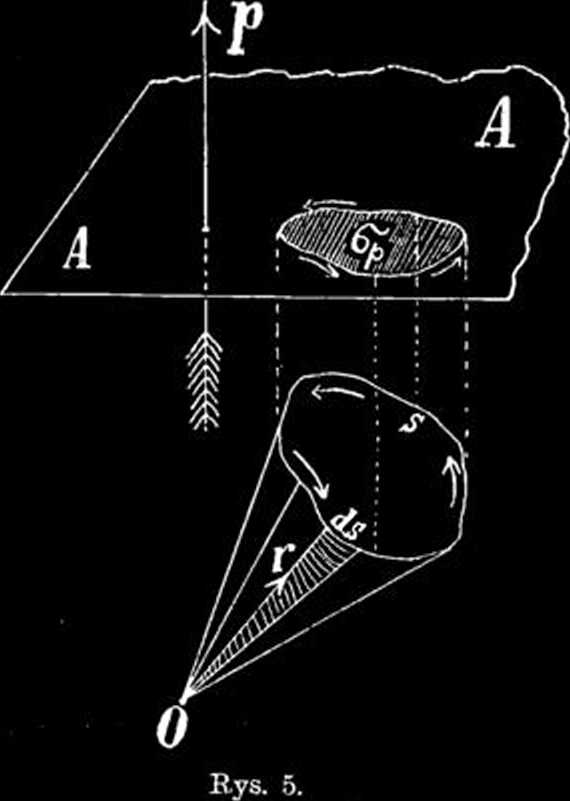
Pomyślmy sobie dowolny obwód, czyli krzywą zamkniętą *• przebiegającą w bryle; niechaj d% będzie jej elementem co do długości i kierunku. Oznaczmy znowu przez 1? prędkość wypadkową dowolnego punktu bryły względem O i rozważmy całkę liniową wektora V wzdłuż obwodu s:

1 = fv d».

Jeżeli bryła obraca się naokoło punktu stałego (Z = O, mamy V = Vpr_y gdzie p jest chwilową prędkością obrotową; w ogólniejszym wypadku bryła może też posiadać prędkość postęjtoiuą w dowowolnyra kierunku, powiedzmy r₀; wówczas j będzie

V = v₀ -f- Vpr_y

gdzie wektor t?₀ jest jednakowy dla wszystkich punktów bryły, t. j. niezależny od r. Przy sługuje on całej bryle, podobnie jak wektor p.

Mamy

v ds = r₀ ds + ds. Vpr = v₀ ds -f- p Vrds\ j lecz    /r₀ ds = v₀J’d% = 0,

1 albowiem całka obejmuje krzywą zamkniętą, czyli zamknięty w sobie łańcuch wektorów elementarnych ds\ ponieważ zaś

wektor p jest jednakowy dla wszystkich punktów bryły, możemy umieścić go przed znakiem całki; otrzymamy przoto

I = pWP, gdzie §^ = /Vrds, czyli    I — pW_Pi

gdzie W_p oznacza składową wektora JW wzdłuż chwilowej osi obrotu.

Natężenie wektora Vrds nie jest niczem innem jak po-dwójnem polem trójkąta Or ds (rys. 5); .1 W_p jest więc polem