8254445110

49

CHARAKTERYSTYCZNE CECHY KRZYWEJ BRUCKNERA.

Z rysunku 36 widzimy, że krzywa otrzymała kształt falisty i że w stosunku do poziomej ah przechodzi przez swe maksymalne i minimalne wartości w punktach b’, c’, d’, e’........i to wszędzie tam, gdzie falista

linja terenu (rys. 35) przecina się z uprzednio zaprojektowanym spadkiem podłużnym AH w punktach B, C, D, E........Widzimy dalej, że

od a do b’ idą nasypy (linja cieńsza), od b’ przez mdoc’ — idą wykopy (linja grubsza), przyczem dla nasypów a—2’—b’ maksymalna wartość ich (kubatura) mierzy się wysokością bb’, a tą samą wysokością bb’ również mierzą się wykopy dla krzywej łb’m, a zatem mówimy, że w punkcie m nasypy zrównoważyły się z wykopami. Inaczej mówiąc (rys. 35), na długości AP pomiędzy profilami A i P kosztem wykopów BMP są wykonane nasypy AKB.

Widzimy dalej, że krzywa Brucknera z poziomą ah twiorzy szereg segmentów, jak: ab’m, mc’d’e’n, nf’p,....., dla których fragmenty krzywej : ab’, c’d’, e’f,......(cieńsze) ze strzałką do góry oznaczają nasypy,

a ze strzałką wdół: b’c’, d’e’, f’g’,..... (grubsize) — oznaczają wykopy.

Wyodrębnimy jeden sygment ABC (rys. 37), dla którego nasypy i wykopy równoważą się.

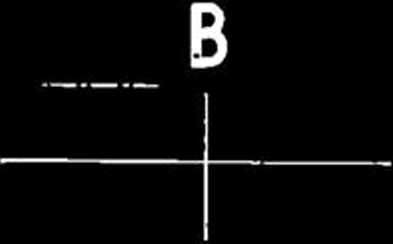
Rys. 37.

Powyżej ustalono, że nasypy AB równoważą się wykopami BC, a ponieważ krzywa ABC w stosunku do prostej AC tworzy zamknięty segment, ustalamy zatem wniosek, że w każdym zamkniętym segmencie następuje równowaga nasypów z wykopami. Poprowadzimy szereg równoległych do podstawy AC, jak: ab, cd, ef, gh,.........Na podstawie tylko

co sformułowanego wniosku możemy powiedzieć, że również następuje równowaga nasypów z wykopami dla segmentów aBb, cBd, eBf,.....