8377355038

xy

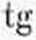
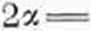
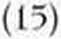
(16)

3. Oś obo j ę t n a p r zy z a 1 o żon i u, ż e siła p o p r z e c z n a p r z e c h o (1 z i p r z e z ś r o cl e k cięż k o ś c i p r z elcro j u.

W tym wypadku prowadzimy zwykle przez środek ciężkości 2 proste: jedna równoległą do cięciwy, drugą prostopadłą. Czasami już te proste uważamy za główne osi bezwładności. Chcąc je znaleźć dokładnie, obliczamy momenty bezwładności wszystkich pól przekrojów obliczeniowych „Ko** względem tych 2 osi l_x i l_y i moment zboczenia l_xy. Kąt nachylenia osi głównych do osi przyjętych da nam wzór:

2 I

lv - 1*

Następnie obliczamy główne momenty bezwładności i kreślimy centralną elipsę bezwładności. Z kolei przez środek ciężkości prowadzimy prostą o kierunku danej siły poprzecznej będzie to kierunek płaszczyzny momentu pary zginającej i dla tej prostej /.nachodzimy przy pomocy prostych stycznych lub przez powinowactwo z kołem przy pomocy metod geometrii wykreślnej średnicę sprzężoną z daną. Będzie to szukana oś obojętna. Prościej można postąpić w ten sposób, że rozkłada się dany moment na 2 kierunki głównych osi bezwładności.

4. Oś oho j ę t n a p r z y założeniu, ż e siła p o p r z e c z n a nie p r z e e h o d z i p r z e z środek sił p o p rzec z n y c h p r z e k r o j u.

W edług zdań niektórych badaczy należy w tym wypadku przesunąć kierunek płaszczyzny momentu pary zginającej równolegle do środka ciężkości i znaleźć oś obojętną jak w przypadku poprzednim przy pomocy elipsy bezwładności. Wynikałoby z tego, że położenie osi obojętnej nie zależy od tego, czy środek sił ścinających pokrywa się ze środkiem ciężkości, czy też nie.

111. Wyznaczanie naprężeń

1. Na p r ę żenią o d m omentó w zgiń a j ą c y eh

Naprężenia te wyznacza się przy pomocy znanych wzorów wytrzymałościowych. Zwykle zgię-

LITERATURA

[1]. Aleksander Grzędziclski. O pewnym wypadku współdziałania dźwigarów skrzydłowych. Sprawozdania IBTL. Nr. 1 (13) 1934.

[2J. W. Billewiez i A. Grzędziclski. Obliczanie skrzydła jednodźwigarowego. Sprawozdania IBTL. Nr. 2 (17). 1935'.

j3| Leon Kirslc, inż.-dok. Sur Ic cnleul des poutres en eaisson. L'A6rolechni({ue — Nr. 169 i Nr. 173, 16 Rocznik. Styczeń i Maj 1937. L'Aćronaulique. Nr. 212 i 210. Styczeń i Mai 1937.

[4) . Dr. Ing. A. Fiippl i Dr. L. Foppl. Drang und Zwang. Monachium 1923.

[5] . C. Weber. Z. £. nngew. Mailu u. Mech. 1924. Tom 4. Sir. 334.

(6) . R. Maillarl. Der Schubmillclpunkl. Sehweiz. Bauz. 1924. Tom 83.

[7] . C. Weber. Z. f. ang. Maili. u. Mech. 1920. t. 6. str. 85.

cic kesonu następuje w 2 płaszczyznach: jednej prostopadłej do cięciwy, drugiej równoległej do cięciwy czyli od 2 obciążeń: normalnego i stycznego. Dla każdego elementu należy znaleźć sumę normalnych naprężeń. Według (8) naprężenia od zginania silami stycznymi nic przewyższają 10% naprężeń od zginania silami normalnymi. Zginanie w płaszczyźnie równoległej do cięciwy w wypadku np. skrzydła wiclodźwigarowcgo będzie głównie obciążać dźwigar pierwszy i ostatni.

2. Naprężenia ścinającc.

Sposób /.nachodzenia naprężeń ścinających od momentów skręcających i od sil poprzecznych podają dokładnie i dla skrzydeł wiclodżwigaro-wycli np. Grzędzielski, Billewiez, Kisielcw, Kbner i inni. Tu tylko podam pewne uproszczenia stosowane przy obliczaniu tych naprężeń.

a)    Przy obliczaniu naprężeń ścinających od momentów skręcających bardzo często stosuje się nawet dla skrzydeł wielodżwigarowych prosty wzór dla przekroju pierścieniowego bez uwzględnienia ścianek wewnętrznych, wychodząc z założenia, że grubość pokrycia (blachy czy sklejki) musi być dostosowaną do grubości „handlowej¹⁴, zmieniającej się przecież skokami. W rezultacie więc obliczenia dokładne i przybliżone prowadzą bardzo często do tych samych praktycznych wyników.

b)    Przy obliczeniu naprężeń ścinających od sil poprzecznych np. skutkiem obciążenia normalnego bierze się pod uwagę tylko ścianki pionowe wewnętrzne, nic uwzględniając tego, że pokrycie również przenosi część tych sił. Zatem we wzorze:

__ QS

za „o‘* przyjmujemy tylko grubości ścianek pionowych wewnęt rznych.

Przy dokładniejszym obliczaniu należałoby uwzględnić zginanie w pionowych płaszczyznach poszczególnych przekrojów, co możnaby nazwać „zginaniem poprzecznym".

Komisja Pomocy Naukowych

KołR Goodotóv St W

(8|. Sprawocznaja knigu po rasczctu samolela pa proezność. Onti NKTR CCCR. 1937.

|9J. W. F. Kisielcw. Obliczenie skrzydeł wielodżwigarowych na skręcanie. Notatki techniczne C. A. G. I. Ńr. 89.

[10] . Dr. Inż. W. Billewiez. Obliczanie skrzydeł wie-lodźwigarowych. Techniczne Nowości Lotnicze. 1930. Nr. 4, 5, 7, 9.

[11] . Inż. S. I. Makarów. Obliczanie cienkościennych konstrukcji, Technika Wozdusznogo Flota. 1935. Nr. 7.

[I2|. M. 7'. Hubcr. Wytrzymałość na czyste zginanie prętów metalowych. Przegląd Techniczny. Nr 7. 1934.

[13|. 11. Ebner. Zur Fesligkcil von Schalen -und Rohr-holmlltlgeln. L.uftłahrliorschung. Lfg. 4/5. B. 14. 1937.

|14). Inż. P. Bielkowicz. Nowe metody obliczeń kadłubów skorupowych. Techniczne Nowości Lotnicze. Kwiecień, maj 1937.

275

ZYCIE TECHNICZNE