Metody matematyczne w technologii materiałów

Krzysztof Szyszkiewicz

C

AŁKOWANIE PRZEZ PODSTAWIENIE

(

CAŁKOWANIE PRZEZ ZAMIANĘ ZMIENNEJ

)

W niektórych przypadkach obliczenie całki

( )

f x dx



może się uprościd, gdy wprowadzimy

pomocniczą zmienną, tzn. zastosujemy podstawienie

( )

x

t





(lub

( )).

t

x





Stosując formalny

rachunek:

( )

dx

t dt







możemy napisad równośd

( )

( ( )) ( ) ,

f x dx

f

t

t dt













(0.1)

gdzie po obliczeniu całki występującej po prawej, która będzie funkcją zmiennej

,

t

podstawiamy

zmienną

x

wyliczoną z zależności

( ).

x

t





P

RZYKŁADY

1) Obliczyd przez podstawienie całkę

2

.

x

xe

dx





W tym przypadku zastosujemy podstawienie

2

.

t

x



(Można też patrzed na tę zamianę jak na

podstawienie

.

x

t



Oba podejścia dają oczywiście ten sam rezultat koocowy.) Obliczamy

2

1

1

(

)

2

.

2

2

dt

x

dx

xdx

dx

dt

dt

x

t













Mamy teraz

2

2

1

1

1

(

)

.

2

2

2

2

x

t

t

t

x

dt

xe

dx

xe

e dt

e

C

e

C

x



















  









2) Obliczyd całkę

1

.

sin

dx

x



W tym przypadku stosujemy specjalne podstawienie, które całkę typu

(sin , cos )

,

R

x

x dx



gdzie

1

2

( ,

)

R x x

jest funkcją wymierną (iloraz dwóch wielomianów), sprowadzi do całkowania funkcji

wymiernej. Podstawienie to ma postad:

tg .

t

x



Do wykonania tego podstawienie będą potrzebne

pewne tożsamości trygonometryczne, które są wyprowadzone poniżej. Bazują one na następujących
podstawowych zależnościach

sin(

)

sin

cos

cos sin ,

cos(

)

cos

cos

sin

sin .

 









 

















(0.2)

W szczególności z powyższych wzorów otrzymujemy wyrażenie na

tg(

)

 



sin(

)

sin

cos

cos sin

tg

tg

tg(

)

.

cos(

)

cos

cos

sin

sin

1 tg tg

 













 

 









 

















(0.3)

Metody matematyczne w technologii materiałów

Krzysztof Szyszkiewicz

W szczególności mamy

2

2

2

2

2

2

2

2

2

2

2

1

2

2

2

2

2 1

2

2

cos

sin

cos

sin

cos 2

cos

sin

1

cos

sin

sin

1

1 tg

1 tg

cos

. Stąd: cos

.

sin

1 tg

1 tg

1

cos






































































Podobnie

2

2

1
2

2

2

2 1

2

2

2sin

cos

2sin

cos

sin 2

2sin

cos

1

cos

sin

sin

2

2tg

2tg

cos

. Stąd: sin

.

sin

1 tg

1 tg

1

cos



























































(0.4)

Ponadto przydatne będą tożsamości

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

sin

1 cos

1

1

tg

1

cos

.

cos

cos

cos

1 tg

sin

sin

tg

tg

, (1 sin

)tg

sin

sin

.

cos

1 sin

1 tg















































 





















(0.5)

Podstawienie

1
2

tg

t

x



daje

2

2

1

1

2

2

2 1

2

2

2

1
2

1

1

1

,

cos

2

2 cos

2

2

2 cos

.

1 tg

1

x

dt

dx

dx

x

x

dt

dx

xdt

t

















Ponadto z (0.4) mamy

1
2

2

2

1
2

2tg

2

sin

,

1 tg

1

x

x

t

x

t









zatem

2

1
2

2

1

1

2

1

ln | |

ln | tg

|

.

sin

2

1

t

dx

dt

dt

t

C

x

C

x

t

t

t









 











3) Obliczyd całkę

2

1

.

1

dx

x





W tym przypadku stosujemy podstawienie

ctg .

x

t



Mamy

2

1

.

sin

dx

dt

t

 

Ponadto

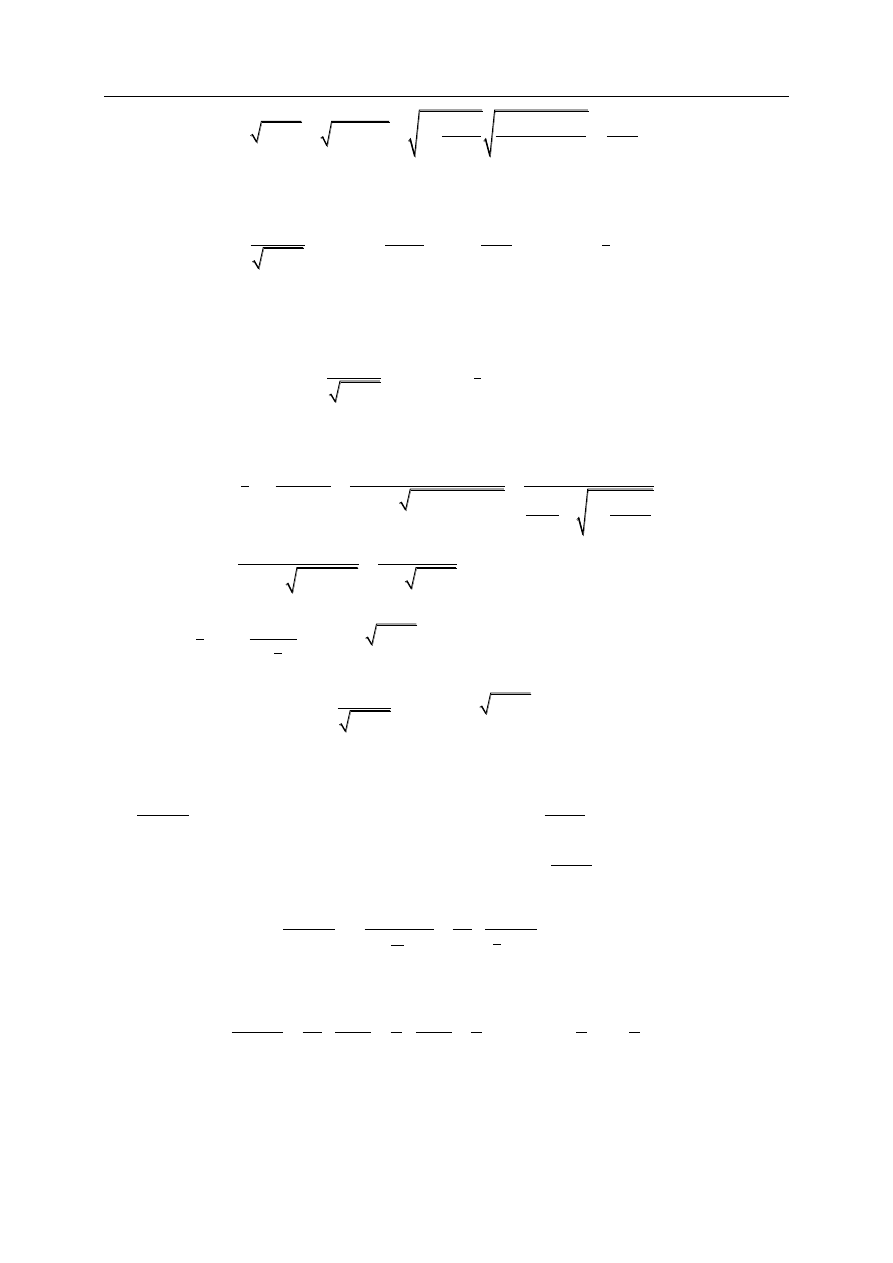
Metody matematyczne w technologii materiałów

Krzysztof Szyszkiewicz

2

2

2

2

2

2

2

cos

sin

cos

1

1

1 ctg

1

.

sin

sin

sin

t

t

t

x

t

t

t

t















Podstawienie jest dla

(0,

),

t





więc w ostatniej równości nie musimy pisad

| sin | .

t

Mamy więc

1
2

2

2

1

1

1

sin

ln | tg

|

.

sin

sin

1

dx

t

dt

dt

t

C

t

t

x





 

 











(0.6)

Ostatnia całka jest na podstawie punktu 2). Musimy jeszcze wrócid do pierwotnej zmiennej

.

x

Formalnie z równości

ctg

x

t



mamy

arcctg

t

x



co daje następujące wyrażenie na całkę

1
2

2

1

ln | tg arcctg |

,

1

dx

x

C

x

 







ale wyrażenie to można zapisad prościej. Mamy bowiem

1
2

2

2

2

2

2

2

sin

sin

1

tg

cos

1

cos

sin

cos

cos

cos

1

sin

sin

1

1

.

ctg

1 ctg

1

t

t

t

t

t

t

t

t

t

t

t

t

t

x

x































Stąd

2

1
2

1
2

1

ln | tg

| ln

ln |

1

| .

| tg

|

t

x

x

t











Ostatecznie otrzymujemy

2

2

1

ln |

1

|

.

1

dx

x

x

C

x













4)

2

2

.

dx

x

a





Obliczenie tej całki sprowadza się do znanej całki

2

arctg

.

1

dx

x C

x









Ta druga całka

wynika oczywiście z pochodnej funkcji arcus tangens:

2

1

(arctg )

.

1

x

x

 



Całkę przepisujemy tak





2

2

2

2

2

2

2

1

( )

1

1

x

x

a

a

a

dx

dx

dx

x

a

a

















i stosujemy podstawienie

/ .

t

x a



Mamy

,

dx

adt



więc

2

2

2

2

2

1

1

1

1

arctg

arctg

.

1

1

dx

adt

dt

x

t

C

C

x

a

a

t

a t

a

a

a







 















C

AŁKOWANIE FUNKCJI WYMIERNYCH

Metody matematyczne w technologii materiałów

Krzysztof Szyszkiewicz

Funkcją wymierna nazywamy funkcję postaci

( )

( )

,

( )

P x

f x

Q x



gdzie

( )

P x

i

( )

Q x

są wielomianami.

Interesowad nas będą tylko funkcje wymierne rzeczywiste, tak więc

x



oraz współczynniki

wielomianów

( )

P x

i

( )

Q x

są rzeczywiste. Oczywiście funkcja wymierna określona jest wszystkich

x



z wyjątkiem miejsc zerowych wielomianu

( ).

Q x

Przykłady funkcji wymiernych

2

5

5

3

2

3

5

3

6

2

1

2

1

,

,

,

,

, 4

1.

1

2

1

1

x

x

x

x

x

x

x

x

x

x

x

x









 



 





Zauważmy, że funkcja wielomianowa jest szczególnym przypadkiem funkcji wymiernej.

Obliczenie całki

( )

( )

P x

dx

Q x



z funkcji wymiernej jest „w zasadzie możliwe” pod warunkiem, że

potrafimy wyznaczyd pierwiastki wielomianu

( ).

Q x

Inaczej mówiąc całka ta wyraża się poprzez

funkcje elementarne oraz pierwiastki równania

( )

0.

Q x



Aby obliczyd całkę funkcji wymiernej, rozkładamy ją na tzw. ułamki proste, które można już całkowad
w sposób elementarny. Ułamki proste są to wyrażenia wymierne następującej postaci

2

2

,

gdzie

4

0 oraz

,

.

(

)

(

)

m

n

A

Bx C

b

c

n m

x

x

bx c





 













(0.7)

Pierwszy typ ułamków prostych całkuje się bardzo prosto:

1

(

)

,

dla

1,

1

(

)

ln |

|

,

dla

1.

m

m

A

x

C

m

A

dx

m

x

x

C

m







 











  

















Na przykład

4 1

4

3

5

5

5

(

2)

.

(

2)

4 1

3(

3)

dx

x

C

C

x

x

 





  





 





Całkowanie ułamków prostych drugiego typu jest bardziej złożone. Po pierwsze warunek

0

 

oznacza, że wyrażenie

2

x

bx c





nie ma miejsc zerowych (pierwiastków) i może byd zapisane

następująco

2

2

,

2

4

b

x

bx c

x









 













(0.8)

gdzie składnik

4



jest dodatni. Mamy więc

2

2

2

2

2

,

1 .

2

4

4

b

x

b

x

bx c

x



























 

































(0.9)

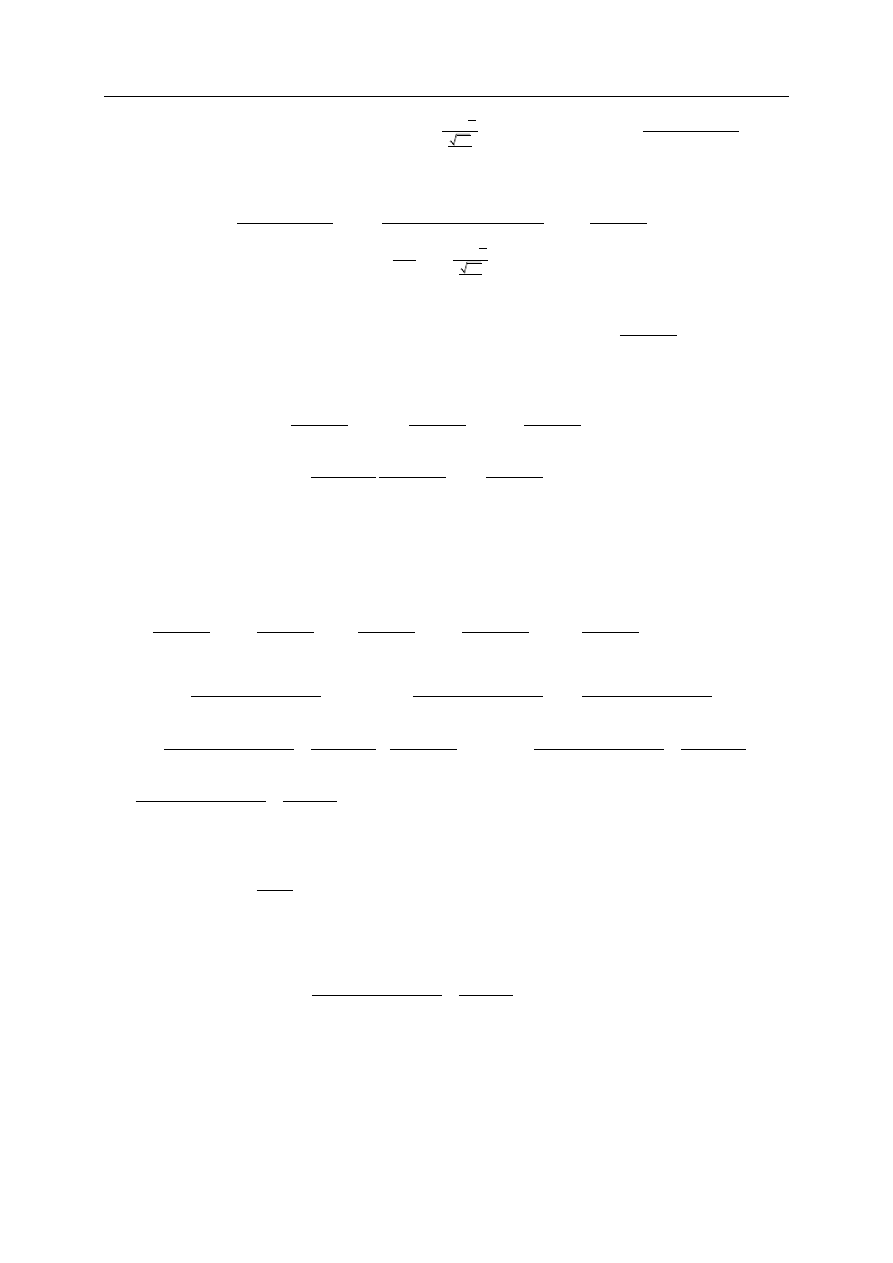
Metody matematyczne w technologii materiałów

Krzysztof Szyszkiewicz

Stosując teraz proste, liniowe podstawienie

2

2

b

x

t







sprowadzamy całkę

2

(

)

n

Bx C

dx

x

bx c









do

prostszej postaci

2

2

2

2

2

.

(

)

(

1)

1

4

n

n

n

n

b

x

Bx C

Bx C

Dt

E

dx

dx

dt

x

bx c

t

































 















 

















(0.10)

Jak widad jedyną trudnością którą teraz mamy jest obliczanie całki postaci

2

.

(

1)

n

Dt

E

dt

t







Całka ta jest

sumą dwóch całek, przy czym jedną z nich oblicza się wprost

2

2

2

2

1

2

1

(

1)

(

1)

(

1)

1

1

.

2(

1) (

1)

(

1)

n

n

n

n

n

Dt

E

t

dt

D

dt

E

dt

t

t

t

t

D

E

dt

n

t

t





















 













Ostatnią całkę można – całkując przez części – sprowadzid do pewnej następującej zależności
rekurencyjnej

2

2

2

2

2

2

1

2

1

1

2

1

2

1

2

1

1

2

1

2

1

1

1

1

(

1)

(

1)

(

1)

(

1)

(

1)

1

1

2(

1)(

1)

2(

1)(

1)

2(

1)(

1)

1

1

2(

1)(

1)

2(

1) (

1)

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

t

t

t

I

dt

dt

dt

dt

t

dt

t

t

t

t

t

t

I

t

dt

I

t

dt

n

t

n

t

n

t

t

I

dt

I

n

t

n

t





































































 



 



 















 



 



















1

1

2

1

1

2

1

1

2(

1)(

1)

2(

1)

2

3

.

2(

1)(

1)

2(

1)

n

n

n

n

t

I

n

t

n

t

n

I

n

t

n















 



 



 



 





Ponadto mamy

1

2

1

arctg

.

1

I

dt

t

C

t











Podsumowując mamy

1

2

1

2

3

,

dla

1,

2(

1)(

1)

2(

1)

arctg

,

dla

1.

n

n

n

t

n

I

n

n

t

n

I

t

C

n















 





 









(0.11)

P

RZYKŁADY

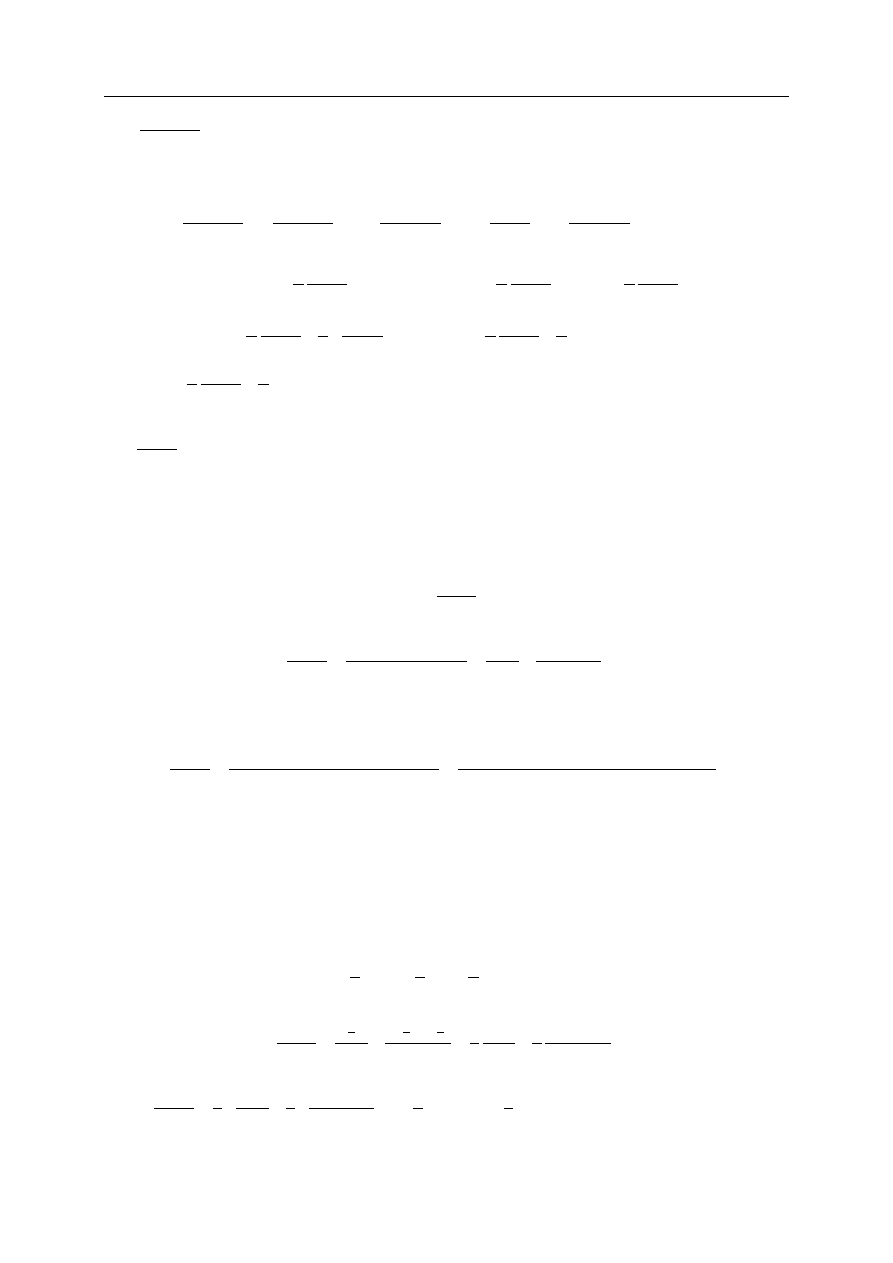
Metody matematyczne w technologii materiałów

Krzysztof Szyszkiewicz

1)

2

2

.

(

1)

dx

x





Możemy tę całkę obliczyd tak jak się wyprowadza zależnośd (0.11) lub po prostu

skorzystad z tych wzorów.

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

1

(

1)

(

1)

(

1)

1

(

1)

1

1

1

1

1

1

arctg

arctg

2

1

2

1

2

1

1

1

1

1

1

=arctg

arctg

arctg

2

1

2

1

2

1

2

1

1

arctg .

2

1

2

dx

x

x

dx

x

dx

dx

x

dx

x

x

x

x

x

x

x

dx

x

x

x

dx

x

x

x

x

x

x

dx

x

x

x

x

x

x

x

x































































































































2)

3

.

1

dx

x





Dokonujemy rozkładu mianownika na czynniki nierozkładalne

3

2

1 (

1)(

1),

x

x

x

x

 



 

a następnie szukamy rozkładu funkcji wymiernej

3

1

1

x



na ułamki proste postaci (0.7):

3

2

2

1

1

.

1

(

1)(

1)

1

1

A

Bx C

x

x

x

x

x

x

x













 



 

Stąd mamy

2

2

3

2

3

1

(

1) (

)(

1)

(

)

(

)

(

)

,

1

(

1)(

1)

1

A x

x

Bx C x

A B x

A B C x

A C

x

x

x

x

x

  







   













 



co po porównaniu współczynników wielomianów z licznika daje

0,

0,

1.

A

B

A B C

A C

 



   



  



Rozwiązaniem tego układu jest

1

1

2

,

,

,

3

3

3

A

B

C



 



zatem

1

1

2

3

3

3

3

2

2

1

1 1

1

2

,

1

1

1

3

1

3

1

x

x

x

x

x

x

x

x

x





 













 



 

skąd

3

2

1

1

2

1

1

ln |

1|

.

1

3

1 3

1

3

3

x

dx

dx

dx

x

I

x

x

x

x

 







 





 







Dalej

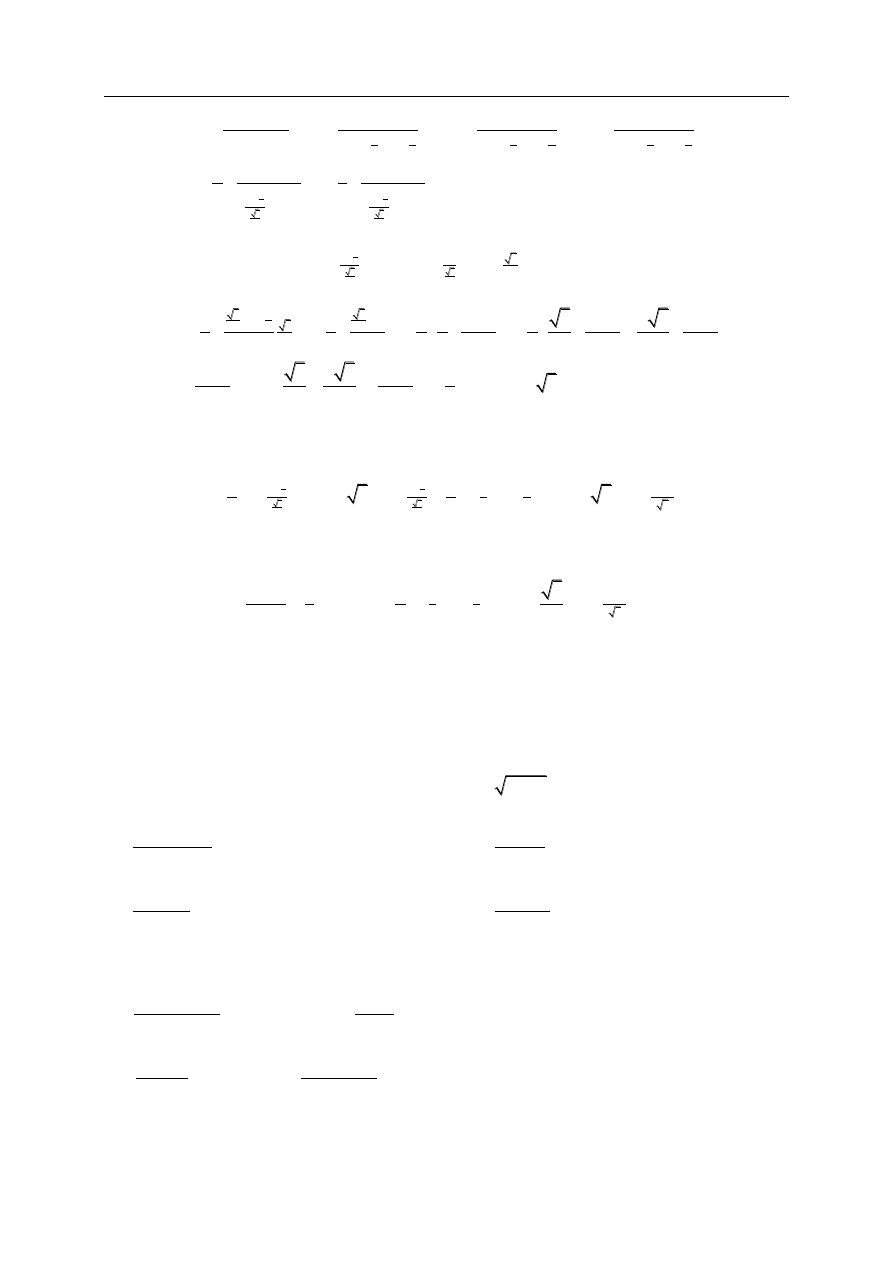
Metody matematyczne w technologii materiałów

Krzysztof Szyszkiewicz

 

 

1

1

2

2

3

3

2

2

2

2

2

2

2

2

3

3

3

1

1

1

2

4

2

4

2

4

1

1

2

2

2

1

(

)

(

)

(

)

4

8

.

3

3

x

x

x

x

x

dx

x

dx

I

dx

dx

dx

x

x

x

x

x

dx





 

 









 





 













 















Teraz stosujemy podstawienie

1
2

3

2

,

x

t





więc

3

2

3

2

.

,

dx

dt

dx

dt





Zatem

2

2

2

2

2

2

2

3

3

1

3

2

2

2

2

2

1

1

1

1

1

1

1

4

8

4 3

4

3

4 3

3

3

3 4

3

4

3

3

4 3

1

ln(

1)

3arctg .

3

3

2

t

dt

t

dt

dt

I

dt

dt

t

t

t

t

t

t

dt

dt

t

t

t

t

















 



  

 









 

 



 

 



























Wracając do „starej” zmiennej

x

otrzymujemy

 

1

1

2

2

3

3

2

2

2

2

2

1

4

4

3

3

3

1

1

ln(

1)

3arctg

ln(

2)

3arctg

.

2

2

x

x

x

I

x

x

C







 

 





 



Ostatecznie mamy

2

2

1

4

4

3

3

3

3

1

1

3

ln |

1|

ln(

2)

arctg

.

1

3

6

3

x

dx

x

x

x

C

x





 



 







Z

ADANIA

A) Obliczyd całki nieoznaczone

1)

7

.

x

e

dx





3)

2

sin

.

xdx



5)

2

.

2

2

dx

x

x







7)

.

1 sin

dx

x





2)

.

ax

xe dx



4)

3

1 5

.

xdx





6)

2

.

3 5

dx

x





8)

.

x

x

dx

e

e







B) Obliczyd podane całki z funkcji wymiernych.

2

3

1)

.

2)

.

2

3

2

1

x

dx

x

x

x











3

4

2

1

3)

.

4)

.

4

2

x

dx

x

x

x

x











