
3.4. Badanie funkcji – analiza pierwszej pochodnej
(1) Wyznaczanie przedziałów monotoniczności funkcji
Twierdzenie
Niech f: x
→
f(x) będzie funkcją określoną w zbiorze D
f
oraz różniczkowalną
w przedziale
( )
b
a,
zawartym w dziedzinie.
a) Jeżeli dla każdego
( )
b
a
x
,
∈
mamy
( )
0
<
′
x
f
, to funkcja
f
jest malejąca w
( )
b
a,
.
b) Jeżeli dla każdego
( )
b
a
x
,
∈
mamy
( )
0
>
′
x
f
, to funkcja
f
jest rosnąca w
( )
b
a,
.
c) Jeżeli dla każdego
( )
b
a
x
,
∈
mamy
( )
0
=
′
x
f
, to funkcja
f
jest stała w
( )
b
a,
.
Praktyczna reguła
Aby wyznaczyć przedziały monotoniczności funkcji różniczkowalnej
f
wystarczy:
•
ustalić dziedzinę funkcji f,
•
wyznaczyć funkcję pochodną
f
′
,
•
wyznaczyć te przedziały, w których pochodna f ’ jest dodatnia (ujemna), czyli
rozwiązać nierówność
( )
0
>
′
x
f
(rozwiązać
( )
0
<
′
x
f
),
•
ustalić, które rozwiązania tych nierówności nie należą do dziedziny funkcji f,
•
zinterpretować otrzymane podzbiory dziedziny: rozwiązania nierówności
f ’(x) > 0 wyznaczają zbiór, w którym funkcja jest rosnąca, a rozwiązania nierówności
f ’(x) < 0, w którym funkcja jest malejąca.
Przykład 1.
Wyznacz przedziały monotoniczności funkcji
f
, określonej w zbiorze liczb
rzeczywistych wzorem
( )
2
4
4
2
3
+
−
+
−
=
x
x
x
x
f
.
D
f
= R
Mamy :
( )
4
8
3
2
−
+
−
=
′
x
x
x
f
;
( )
(
)
0
2
3
2
3
0
4
8
3
0
2
>
−
−
−
⇔
>
−
+
−
⇔
>
′
x
x
x
x
x
f
, więc
( )
∈
⇔
>
′
2
,
3
2
0
x
x
f
;
( )
(
)
(
)
+∞
∪
−
∞
−
∈
⇔
<
−
−
−
⇔
<
′
,
2
3
2
,
0
2
3
2
3
0
x
x
x
x
f
.

Stąd na mocy podanego twierdzenia funkcja
f
jest malejąca w przedziałach:
−
∞
−
3
2
,
oraz
(
)
+∞
,
2
i
f
jest rosnąca w przedziale
2
,
3
2
.
(2) Wyznaczanie ekstremów lokalnych
Definicja
Niech funkcja
f
będzie określona w pewnym otoczeniu punktu x
0
.
Mówimy, że funkcja f w punkcie x
0
ma ekstremum lokalne równe f(x
0
), przy czym;
a) jest to maksimum lokalne, gdy dla każdego punktu x z sąsiedztwa punktu x
0
zachodzi
warunek f(x)
≤
f(x
0
),
b) jest to minimum lokalne, gdy dla każdego punktu x z sąsiedztwa punktu x
0
zachodzi
warunek f(x)
≥
f(x
0
).
Uwaga
Ekstremum funkcji w punkcie x
0
jest pojęciem lokalnym, tzn. związane jest z
zachowaniem się funkcji w pewnym dostatecznie małym otoczeniu punktu x
0
, a nie
zależy od wartości funkcji poza tym otoczeniem. Aby dać temu wyraz mówimy o
ekstremum lokalnym.
Pojęcia te należy odróżniać od pojęcia największej lub najmniejszej wartości funkcji w
pewnym zbiorze. To ostatnie jest pojęciem integralnym, gdyż odnosi się do całego zbioru,
w którym rozpatrujemy funkcję, np. do dziedziny tej funkcji.
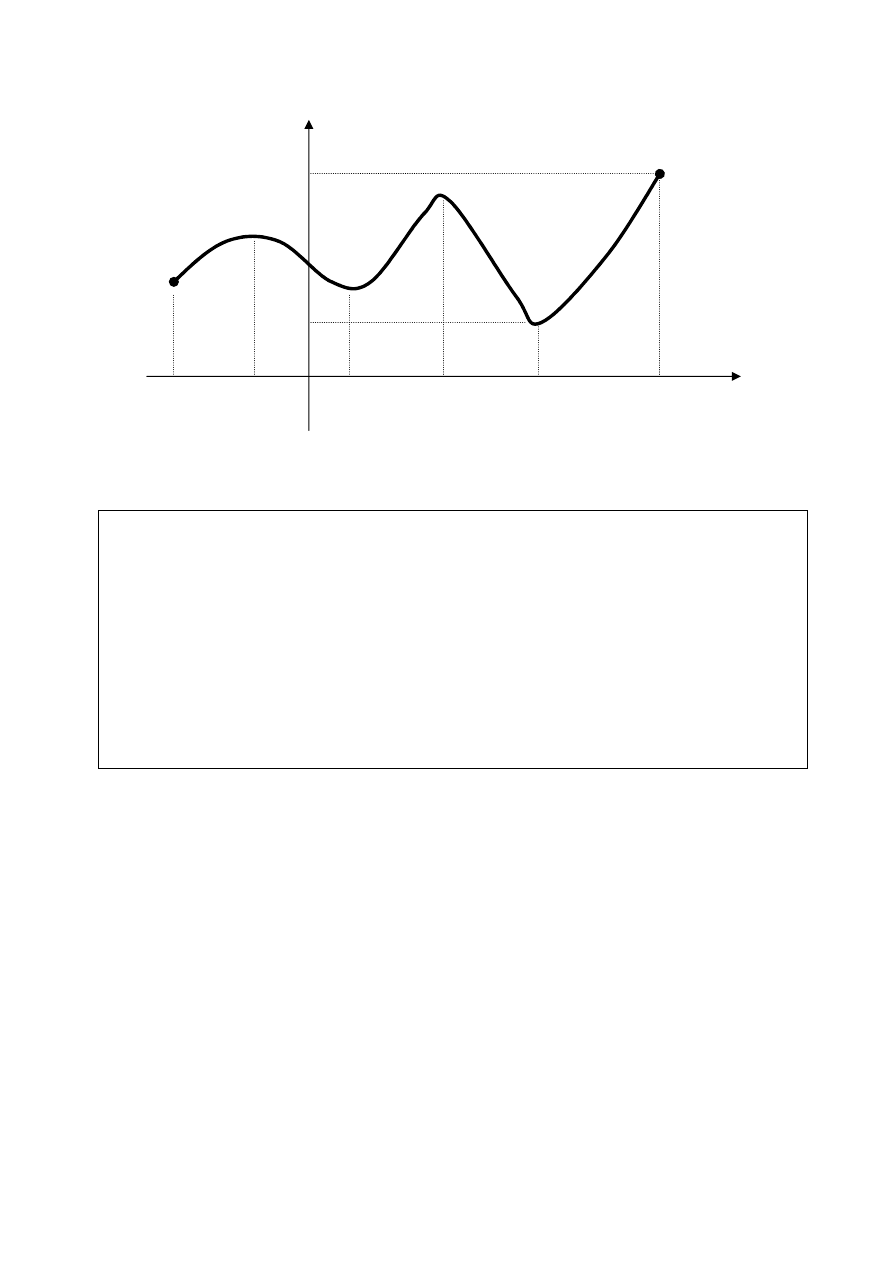
Rysunek przedstawia wykres funkcji określonej w przedziale domkniętym [a, b], ilustruje jej
maksima lokalne: w punkcie x
1
równe f(x
1
), w punkcie x
3
równe f(x
3
), w punkcie b
równe
f(b), minima lokalne: w punkcie x
2
równe f(x
2
), w punkcie a
równe f(a), w punkcie x
4
równe
f(x
4
). Ma jednocześnie wartość największą w punkcie b
równe f(b) oraz najmniejszą w punkcie
a
równe f(a).
Twierdzenie
Jeżeli funkcja f jest różniczkowalna w przedziale (a, b) oraz w punkcie x
0
tego
przedziału jest f ’(x
0
) = 0 oraz w pewnym:
a) podprzedziale ( x
0
-
ε
, x
0
) pochodna f ’ jest dodatnia a w przedziale ( x
0
, x
0
+
ε
)
pochodna f ’ jest ujemna (
ε
> 0) , to w x
0
funkcja ma maksimum lokalne równe
f(x
0
),
b) podprzedziale ( x
0
-
ε
, x
0
) pochodna f ’ jest ujemna a w przedziale ( x
0
, x
0
+
ε
)
pochodna f ’ jest dodatnia, to w x
0
funkcja ma minimum lokalne równe
f(x
0
).
Uwaga
Ciągłość funkcji f w punkcie x
0
oraz istnienie pochodnej f’ różnych znaków w
lewostronnym sąsiedztwie i prawostronnym sąsiedztwie punktu x
0
jest warunkiem
wystarczającym do tego, aby funkcja f miała w tym punkcie ekstremum lokalne.
Praktyczna reguła
Aby wyznaczyć ekstrema lokalne funkcji różniczkowalnej f wystarczy:
•
ustalić dziedzinę D
f
funkcji f,
•
wyznaczyć funkcję pochodną
f
′
,
•
rozwiązać równanie
( )
0
=
′
x
f
, czyli wyznaczyć miejsca zerowe funkcji pochodnej f’,
•
jeśli równanie to nie ma rozwiązań, to funkcja
f
nie posiada ekstremów lokalnych,
y
x
f(x
4
)
f(b)
maksimum lokalne
maksimum lokalne
maksimum lokalne
minimum lokalne
minimum lokalne
minimum lokalne
x
2
x
3
x
4
x
1
b
a

•
gdy istnieją rozwiązania tego równania ustalić, które z nich należą do dziedziny D
f
funkcji f, wybrać te rozwiązania,
•
zbadać znak pochodnej f ’ w pewnym otoczeniu każdego argumentu x
0
, który jest
rozwiązaniem równania f ’(x) = 0, czyli rozwiązać nierówności f ’(x) > 0, f ’(x) < 0,
•
ustalić, czy w otoczeniu punktu x
0
pochodna f ’ zmienia znak,
•
zinterpretować otrzymany rezultat:
a) jeśli w otoczeniu punktu x
0
pochodna f ’ zmienia znak, wówczas w x
0
funkcja ma
ekstremum lokalne (ustalić, czy jest to maksimum, czy minimum lokalne oraz
wyznaczyć jego wartość),
b) jeśli w otoczeniu punktu x
0
pochodna f ’ nie zmienia znaku, wówczas w x
0
funkcja
nie ma ekstremum lokalnego.
Przykład 2.
Wyznacz ekstrema lokalne funkcji
f
określonej wzorem
( )
4
3
2
3
+
−
=
x
x
x
f
.
Oczywiście D
f
= R.
Mamy:
( )
x
x
x
f
6
3
2
−
=
′
, więc
( )
(
)
2
0
0
2
3
0
=
∨
=
⇔
=
−
⇔
=
′
x
x
x
x
x
f
;
( )
(
)
(
) (
)
+∞
∪
∞
−
∈
⇔
>
−
⇔
>
′
,
2
0
,
0
2
3
0
x
x
x
x
f
;
( )
( )
2
,
0
0
∈
⇔
<
′
x
x
f
.
Wynik badania wartości i znaków pochodnej
f
′
przedstawiamy schematycznie:
0 2
Stąd i z podanego twierdzenia wynika, że funkcja
f
osiąga minimum lokalne w punkcie 2
(
2
0
=
x
) równe
( )
0
2
min
=
f
oraz
f
osiąga maksimum lokalne w 0 (
0
0
=
x
) równe
( )
4
0
max
=
f
.
Praktyczna reguła
W zadaniach praktycznych (i nie tylko) ważne jest wyznaczenie najmniejszej i
największej wartości funkcji
f
w przedziale domkniętym [a, b] zawartym w jej dziedzinie. W
tym celu wystarczy:
−
+
+
−
+
+
0
0

0
1
wyznaczyć pochodną
f
′
i rozwiązać równanie
( )
0
=
′
x
f
,
0
2
jeśli równanie
( )
0
=
′
x
f
ma rozwiązania należące do przedziału ( a, b), to obliczyć
wartość funkcji
f
dla wyznaczonych rozwiązań,
0
3
obliczyć wartości: f(a), f(b) funkcji f
0
4
spośród wartości funkcji obliczonych w punktach
0
2
i
0
3
wybrać wartość najmniejszą
i największą.
Przykład 3.
Wyznacz ekstrema lokalne, wartość największą, najmniejszą funkcji f określonej wzorem
f(x) = 2x
3
+ 3x
2
– 12x + 7.
Rozwiązanie
a) Dziedziną funkcji f jest zbiór liczb rzeczywistych.
b) Pochodna funkcji f(x) = 2x
3
+ 3x
2
– 12x + 7 wynosi f’(x) = 6x
2
+6x - 12 = 6(x+2)(x-1).
c) f’(x) = 0
⇔
x = -2 lub x = 1.
d) f’(x) < 0 w przedziale (-2, 1), a w obu przedziałach ( -
∞
, -2) oraz (1,
∞
) pochodna f’ jest
dodatnia.
e) Na mocy twierdzenia, funkcja f jest rosnąca w przedziale ( -
∞
, -2), następnie maleje w
przedziale (-2, 1) i znowu rośnie w przedziale (1,
∞
). Wobec tego w punkcie x = -2 osiąga
maksimum lokalne równe f(-2) = 27, a w punkcie x = 1minimum lokalne równe f(1) = 0.
f) Ponieważ
∞
→
x
lim (2x
3
+ 3x
2
– 12x + 7) =
∞
oraz
−∞
→
x
lim (2x
3
+ 3x
2
– 12x + 7) = -
∞
, zatem
funkcja f nie ma ani wartości najmniejszej, ani wartości największej.
Odpowiedź
Funkcja f ma w punkcie -2 maksimum lokalne równe 27 oraz w punkcie 1 ma minimum
lokalne równe 0. Nie ma wartości najmniejszej, ani największej.
Przykład 4.
Wyznacz najmniejszą i największą wartość funkcji
( )
x
x
x
f
+
=
3
2
w przedziale [
−
1, 4].
0
1
Dziedziną D
f
funkcji
f jest R\ {
−
3}; zatem [
−
1, 4]
⊂
D
f
.

2
o
Dla
3
−
≠
x
,
( )
(
)
(
)
(
)
2
2
2
2
3
6
3
3
2
x
x
x
x
x
x
x
x
f
+
+
=
+
−
+
=
′
.
3
o
( )
6
0
0
6
0
2
−
=
∨
=
⇔
=
+
⇔
=
′
x
x
x
x
x
f
, ale tylko
(
)
4
,
1
0
−
∈
, więc obliczamy
( )
0
0
=
f
.
4
o
( )
2
1
1
3
1
1
=
−
=
−
f
,
( )
7
16
4
3
16
4
=
+
=
f
.
5
o
Z rozważań w punktach 3
o
i 4
o
wynika, że najmniejsza wartość
f
w tym przedziale jest
równa
0
, a największa
7
16
.
Zadania do samodzielnego rozwiązywania
Zadanie 1.
Wyznacz przedziały monotoniczności funkcji f, gdy:
a) f(x) = x
3
– 7,5 x
2
+ 18x +4 , b) f(x) = 3 x
4
- 6x
2
+ 7 , c) f(x) = 0,2 x
5
-
3
1
x
3
+ 11 ,
d) f(x) =
4
2
−
x
x
, e) f(x) =
2
3
−
x
x
, f) f(x) =
1
2
2
2
+
x
x
, g) f(x) = x+
5
4
−
x
.
Zadanie 2.
Wyznacz przedziały monotoniczności funkcji f, gdy:
a) f(x) = x + sin x , dla x
∈
[ 0, 2
π
] , b) f(x) = x – cos x, dla x
∈
[ 0, 2
π
] ,
c) f(x) = sin x + cos x dla x
∈
[ 0, 2
π
] , d) f(x) = tg
2
x dla x
∈
[-
π
/2 ,
π
/2 ] ,
e) f(x) = x ln x dla x > 0 , f) f(x) = x (ln x)
-1
dla 0 < x
≠
1.
Zadanie 3.
Wyznacz te wartości parametru a, dla których funkcja f w całym zbiorze R jest:
a) rosnąca, f(x) = x
3
+ ax
2
– ax + 2 ,
b) malejąca , f(x) = - x
3
+ 6(a+2)x
2
+60(a+2)x + 12 .
Zadanie 4.
Wyznacz ekstrema lokalne funkcji f, jeżeli:
a) f(x) = x
3
– 6x
2
+ 9x – 4 , b) f(x) = - x
4
+2x
2
, c) f(x) = x x – 3x + 1 ,
d) f(x) =
2
2
x
x
−
, e) f(x) = x
2
(x
2
– 4)
3
, f) f(x) = x x –
3
5
,
1
x
.
Zadanie 5.
Wyznacz ekstrema lokalne funkcji f, jeżeli:
a) f(x) =
x
x
−
3
3
, b) f(x) =
4
2
+
x
x
, c) f(x) =
2
2
9
x
x
−
, d) f(x) = x + x
-1
,
e) f(x) =
x
x
2
1
2
−
, f) f(x) =
1
2
+
x
x
, g) f(x) = x ln x , h) f(x) = x e
-x
.
Zadanie 6.
Wyznacz największą i najmniejszą wartość funkcji f w podanym przedziale:
a) f(x) = 2x
3
+3x
2
– 12x +1 , [-1, 5], b) f(x) = x
2
(x
2
-1) , [-2, 3] ,
c) f(x) =
x
4
5
−
, [-1, 1], d) f(x) = 2x
4
– x , [-1,1] , e) f(x) = x(32 + x
3
) , [-3, 1],
f) f(x) =
2
1
2
x
x
+
,[-2, 2] , g) f(x) =
2
2
4
3
x
x
x
−
−
, [-1,1] , h) f(x) = x
2
ln x, [-1, e].
Zadanie 7.
Wyznacz przedziały monotoniczności i ekstrema lokalne funkcji
f
, jeśli:
a)
( )
4
3
2
3
−
+
=
x
x
x
f
, b)
( )
2
3
2
2
−
+
−
=
x
x
x
x
f
.
Zadanie 8.
Wyznacz najmniejszą (m) i największą (M) wartość funkcji
f
, jeśli:
a)
( ) (
)
x
x
x
f
4
−
=
, w przedziale [0, 4], b)
( )
x
x
x
f
−
−
=
4
2
1
, w przedziale [0, 2].
Odpowiedzi
Zad. 1.: a) rosnąca w ( -
∞
, 2], [3,
∞
), malejąca w [2,3], b) rosnąca w [-1,0] , [1,
∞
),
malejąca w ( -
∞
, -1], [0,1], c) rosnąca w ( -
∞
, -1], [1,
∞
), malejąca w [-1,1],
d) malejąca w ( -
∞
, -2), (2,
∞
), (-2,2), e) rosnąca w (1,5; 2), (2,
∞
), malejąca
w ( -
∞
, 1,5), f) rosnąca w ( -
∞
, -1], (0, 1), malejąca w (-1, 0), (1,
∞
),
g) rosnąca w ( -
∞
, 3), (7,
∞
), malejąca w (3,5), (5,7).
Zad. 2.: a) rosnąca, b) rosnąca, c) rosnąca w (0; 0,25
π
), (1,25
π
; 2
π
) ,
malejąca w (0,25
π
; 1,25
π
), d) rosnąca w (0: 0,5
π
), malejąca w (- 0,5
π
;0),
e) rosnąca w [e
-1
,
∞
) , malejąca w (0, e
-1
] , f) rosnąca w [e,
∞
), malejąca w (0,1), (1,e).
Zad. 3.: a) a
∈
(-3, 0) , b) a
∈
(-7,-2) .
Zad. 4.: a) max: f(1) = 0, min: f(3) = - 4, b) max: f(1) = f(-1) = 1, min: f(0) = 0,
c) min: f(4) = - 3, d) max: f(1) = 1, e) max: f(0) = 0, f) min: f(
9
1
) =
27
2
−
.
Zad. 5.: a) max: f(4,5) = 60,75, b) min: f(-2) = -0, 25 ,max: f(2) = 0,25,
c) min: f(0) = 0, d) max: f(0) = 0, e) max: f(1) = -1, f) nie ma ekstremum,
g) min: f(e
-1
) = - e
-1
, h) max: f(1) = e
-1
.
Zad. 6.: a) max: f(5) = 266, min: f(-1) = - 6, b) max: f(3) = 72,
min: f(0) = f(-1)= f(1) = 0, c) max: f(-1) = 3, min: f(1) = 1,
d) max: f(-1) = 3, min: f(0,5) = - 0, 375, e) max: f(1) = 33, min: f(-2) = - 48,
f) max: f(1) = 1, min: f(-1) = - 1, g) max: f(1) =-
3
2
, min: f(-1) = -
3
4
,
h) max: f(e) = e
2
, min: f(1) = 0.
Zad.7.: a)
x
−
∞
….
−
1 … 0 … 1 …
∞
f’
−
0 + 0
−
0 +
f
1 4 1
Funkcja f jest malejąca w przedziałach (
−
∞
,
−
1), (0, 1), rosnąca w przedziałach
(
−
1, 0), (1,
∞
) ; f
max
(0) = 4; f
min
(
−
1) = 1, f
min
(1) = 1.
b)
x
−
∞
…. 2
−
3
… 2 … 2+
3
…
∞
f’
+ 0
−
*
−
0 +
f
2
−
2
3
* 2 +2
3
D
f
= R\{2} ; funkcja f jest rosnąca w przedziałach (
−
∞
, 2
−
3
), (2 +
3
,
∞
),
malejąca w przedziałach ( 2
−
3
, 2), (2, 2 +
3
); f
max
(2
−
3
) = 2
−
2
3
;
f
min
(2 +
3
) = 2 +2
3
.
Zad. 8.: a) M = 0; m =
9
3
16
−
; b) M = 0,25 ; m =
−
1,5.
Wyszukiwarka
Podobne podstrony:
Testowanie, TEST Badania funkcjonalne
3 5 Badanie funkcji 2
Badanie funkcjonalne narzÄ…du ruchu
a6 badanie funkcji Nieznany (2)
060 Tw de L'Hospitala, badanie funkcji
5 Badanie funkcji id 39644 Nieznany (2)
Badanie Funkcji Logicznych
Badanie funkcji
Badanie funkcji
Badanie funkcji2c
arkusz BADANIE FUNKCJI
matematyka badanie funkcji, WSEI, SEMESTR 2, Matematyka
badanie funkcji
badanie funkcji przyklad
08 Badanie funkcji organizmu zdrowego człowieka
am przyklady badanie funkcji lista6
Badanie funkcji
badanie funkcji różniczkowalnych
badanie funkcji
więcej podobnych podstron