WM
5. Ćwiczenie projektowe numer 5 – przykład 1
1
5. Ćwiczenie projektowe numer 5 – przykład 1
5.1. Ćwiczenie projektowe numer 5
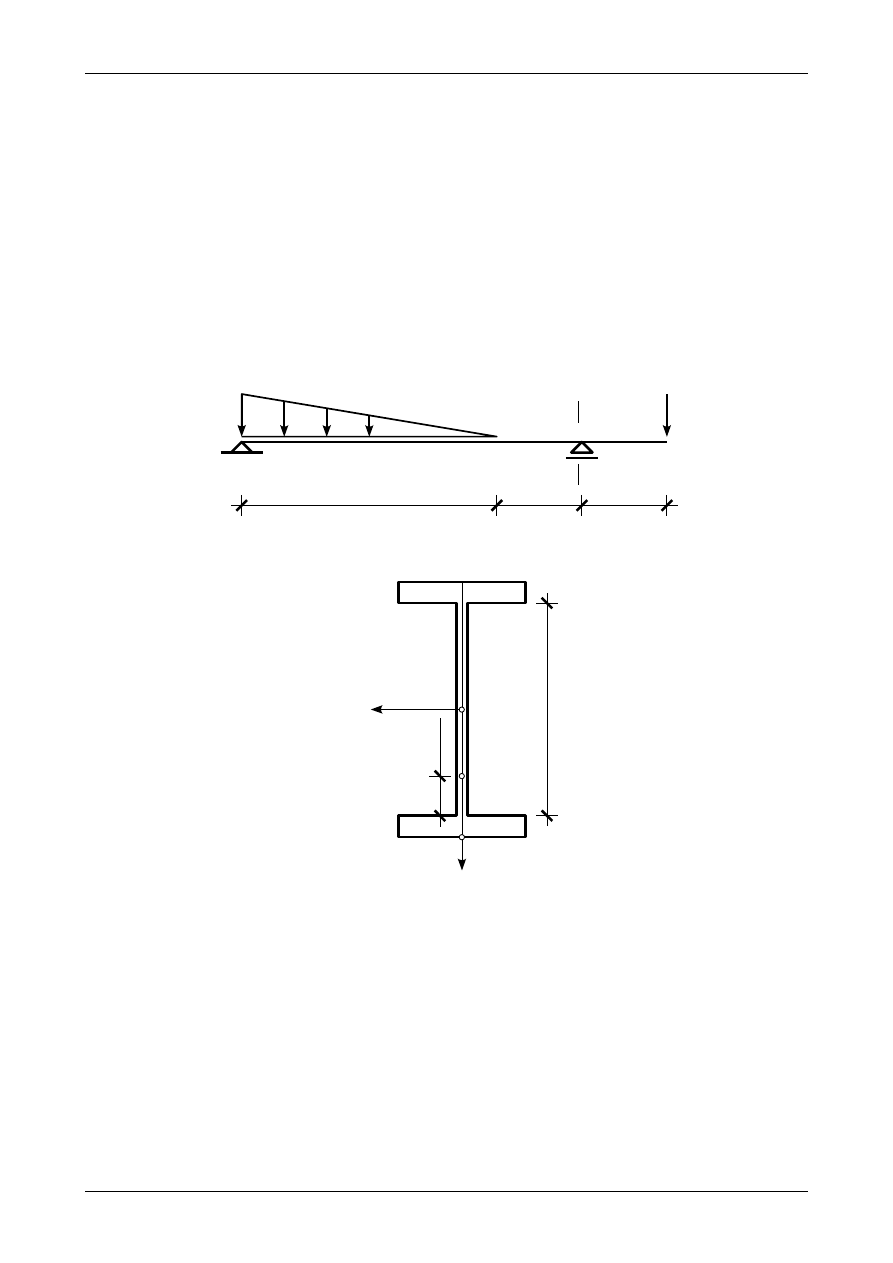
Wykazać geometryczną niezmienność oraz narysować wykresy siły poprzecznej i momentu zginają-
cego dla belki przedstawionej na rysunku 5.1. Zaprojektować przekrój pręta jako blachownicę dwuteową.
W przekroju
α
-
α
wyznaczyć wartości oraz zwroty sił przekrojowych. Narysować wykresy naprężenia
normalnego
σ
X
oraz naprężeń stycznych
τ
XZ
i
τ
XY
. W punktach A, B i C, przedstawionych na rysunku 5.2,
wyznaczyć kierunek oraz naprężenia główne. Naprężenia w układach ZX oraz osi głównych przedstawić
graficznie na elementarnych kwadratach. W punkcie B wyznaczyć stan odkształcenia odpowiadający
stanowi naprężenia w układzie ZX oraz w układzie osi głównych. Na koniec w punkcie B wyznaczyć
naprężenia zredukowane według hipotez Treski i H-M-H (Hubera).
Wytrzymałość stali, z której wykonana jest belka złożona, przyjąć równą 215 MPa. Wartość modułu
Younga wynosi 205 GPa natomiast wartość współczynnika Poissona 0,3.
A
B
C
D
12,0 kN
24,0 kN/m
6,0
2,0
2,0
[m]
α
α
Rys. 5.1. Belka
Y=Y
gl
Z=Z
gl
h
S
A
B
C
0,
3∙
h
S
Rys. 5.2. Przekrój belki
5.2. Analiza kinematyczna belki
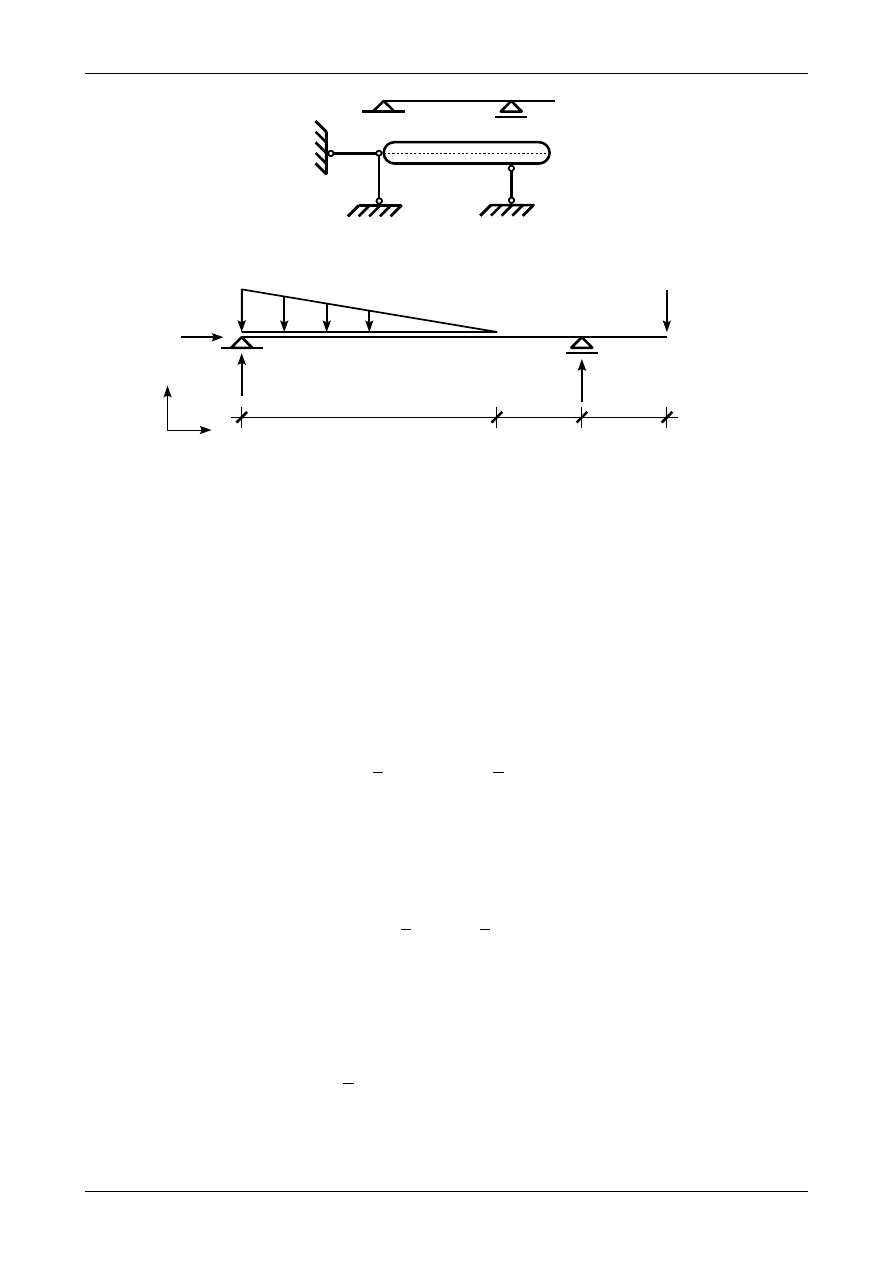
Rysunek 5.3 przedstawia belkę prostą traktowaną w analizie kinematycznej jako płaską tarczę
sztywną. Jak widać tarcza sztywna posiada trzy stopnie swobody. Tarcza ta jest podparta trzema prętami
podporowymi 1, 2 i 3. Wszystkie te więzy odbierają razem trzy stopnie swobody. Został więc spełniony
warunek konieczny geometrycznej niezmienności. Belka może więc być układem geometrycznie
niezmiennym i statycznie wyznaczalnym. Tarcza numer I jest podparta trzema prętami podporowymi numer
1, 2 i 3, których kierunki nie przecinają się w jednym punkcie. Został więc spełniony także i warunek
dostateczny geometrycznej niezmienności dla tej tarczy sztywnej. Jest więc ona geometrycznie niezmienna
i statycznie wyznaczalana.
Dr inż. Janusz Dębiński
BNS-I
WM
5. Ćwiczenie projektowe numer 5 – przykład 1
2
1
2
3
I
A
C
D
Rys. 5.3. Belka jako tarcza sztywna
A
B
C
D
12,0 kN
24,0 kN/m
6,0
2,0
2,0
[m]
X
Y
V
A
H
A
V
C
Rys. 5.4. Założone zwroty reakcji podporowych
5.3. Wyznaczenie reakcji podprowych
Rysunek 5.4 przedstawia założone zwroty reakcji podporowych. Pozioma reakcja na podporze A
wynosi
X =H
A
=
0
H
A
=
0,0kN
.
Pionowa reakcja na podporze A wynosi
M
C
=
V
A
⋅
8,0−
1
2
⋅
24,0⋅6,0⋅
2,0
2
3
⋅
6,0
12,0⋅2,0=0
V
A
=
51,0 kN
.
Pionowa reakcja na podporze C wynosi
M
A
=−
V
C
⋅
8,0
1
2
⋅
24,0⋅6,0⋅
1
3
⋅
6,012,0⋅10,0=0
V
C
=
33,0 kN
.
Równanie sprawdzające ma postać
Y =V
A
V
C
−
1
2
⋅
24,0⋅6,0−12,0=51,033,0−72,0−12,0=0
.
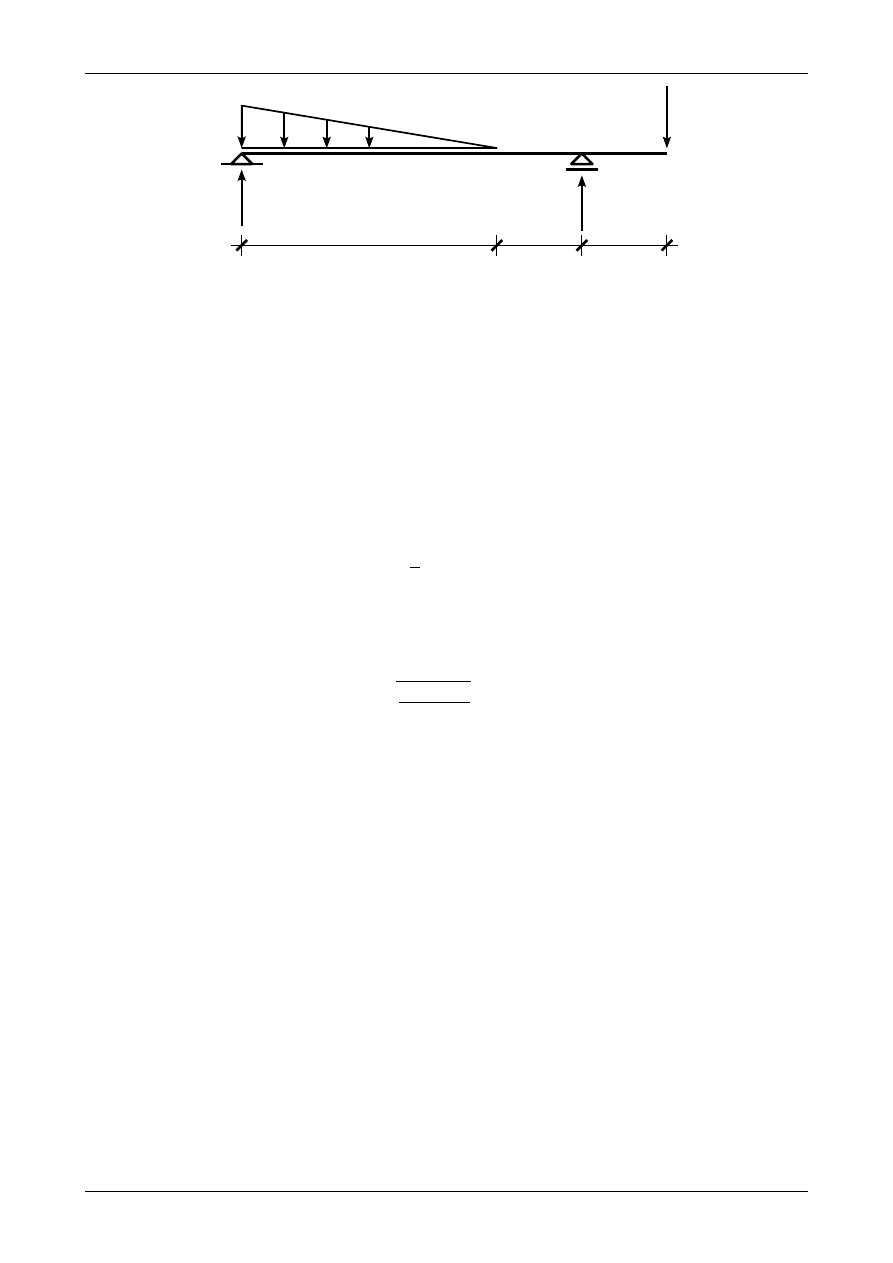
Rysunek 5.5 przedstawia prawidłowe wartości i zwroty reakcji podprowych.
Dr inż. Janusz Dębiński
BNS-I
WM
5. Ćwiczenie projektowe numer 5 – przykład 1
3
A
B
C
D
12,0 kN
24,0 kN/m
6,0
2,0
2,0
[m]
51,0 kN
33,0 kN
Rys. 5.5. Prawidłowe wartości i zwroty reakcji podporowych
5.4. Wykres siły poprzecznej
W przedziale AB siła poprzeczna jest funkcją kwadratową natomiast w pozostałych przedziałach
funkcją stałą. Wartość siły poprzecznej w punkcie A wynosi
T
A
=
51,0 kN
.
Wartość siły poprzecznej z lewej strony punktu B wynosi
T
B
L
=
51,0−
1
2
⋅
24,0⋅6,0=−21,0 kN
.
Miejsce zerowe siły poprzecznej znajduje się w odległości
x
L
=
2⋅21,0⋅6,0
24,0
=
3,240 m
od punktu B. W punkcie tym znajduje się również ekstremum tego wykresu. Wartość siły poprzecznej
z prawej strony punktu B wynosi
T
B
P
=−
21,0 kN
.
Wartość siły poprzecznej w przedziale BC i z lewej strony punktu C wynosi
T
BC
=
T
C
L
=−
21,0 kN
.
Wartość siły poprzecznej z prawej strony punktu C wynosi
T
C
P
=−
21,033,0=12,0 kN
.
Wartość siły poprzecznej w przedziale CD wynosi
Dr inż. Janusz Dębiński
BNS-I
WM
5. Ćwiczenie projektowe numer 5 – przykład 1
4
T
CD
=
12,0 kN
.
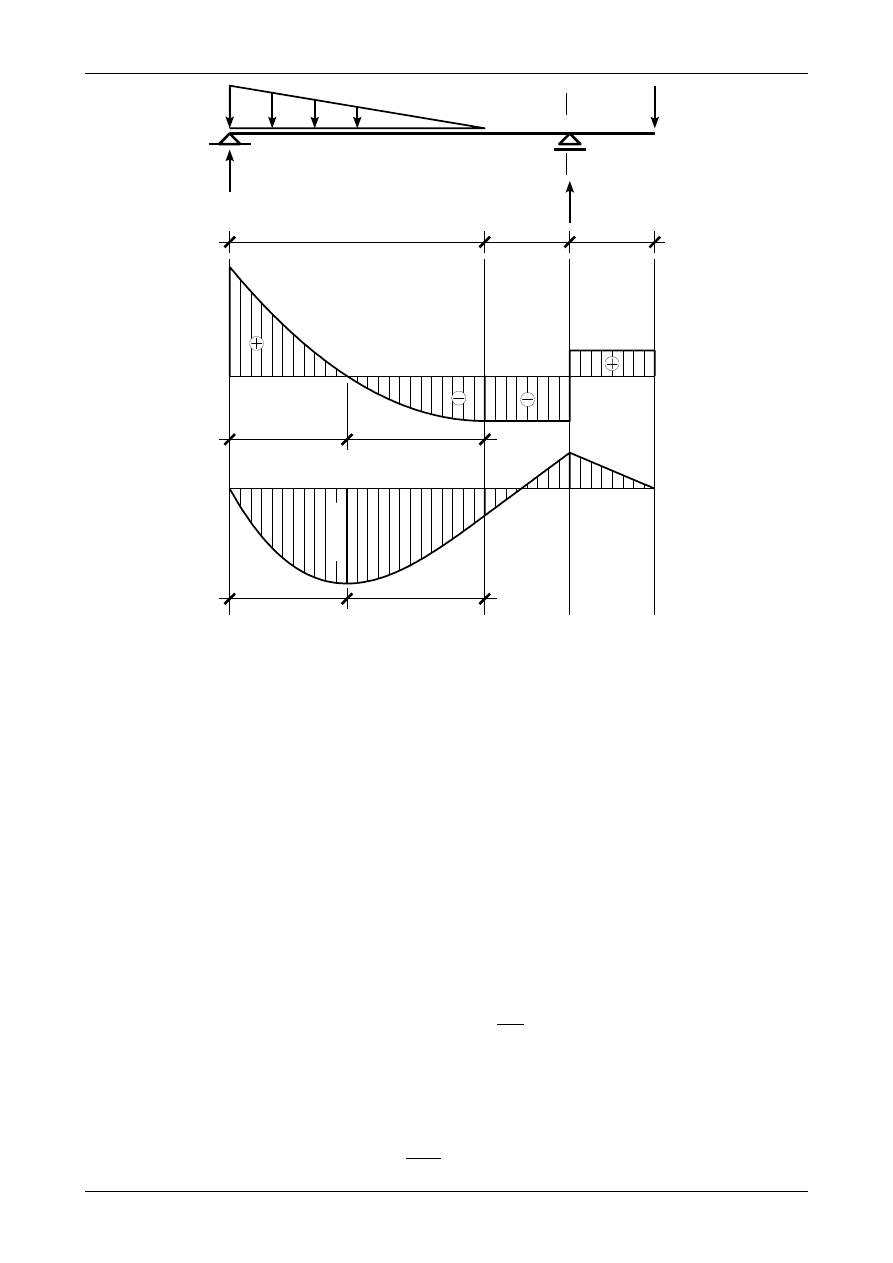
Rysunek 5.11 przedstawia wykres siły poprzecznej w belce.
5.5. Wykres momentu zginającego
W przedziale AB moment zginający jest funkcją trzeciego stopnia natomiast w pozostałych
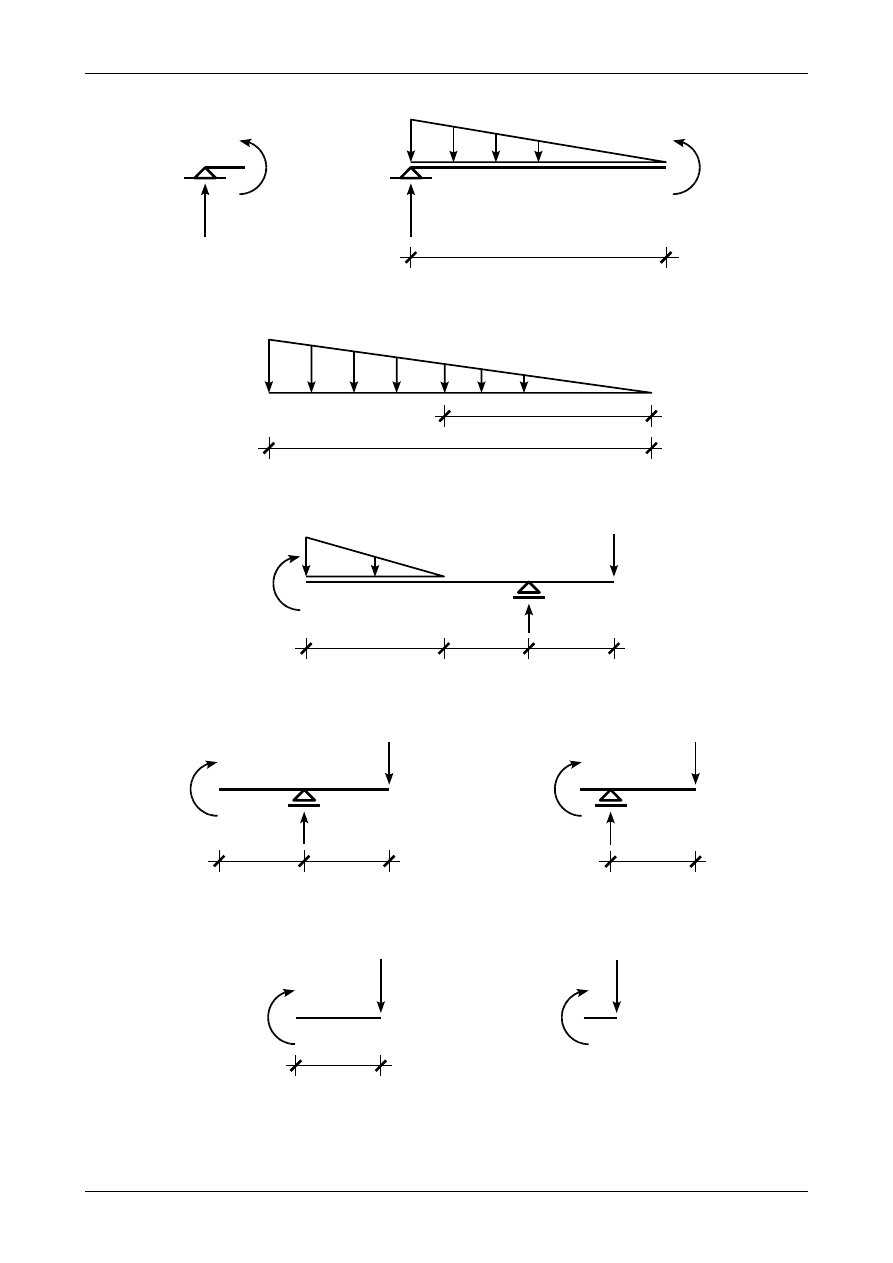
przedziałach funkcją liniową. Zgodnie z rysunkiem 5.6 a) moment zginający w punkcie A wynosi
M
A
=
0,0kNm
.
Zgodnie z rysunkiem 5.6 b) moment zginający z lewej strony punktu B wynosi
M
B
L
=
51,0⋅6,0−
1
2
⋅
24,0⋅6,0⋅
2
3
⋅
6,0=18,0 kNm
.
Zgodnie z rysunkiem 6.7 wartość obciążenia ciągłego w miejscu ekstremum momentu zginającego wynosi
q
1
3,240
=
24,0
6,0
,
q
1
=
12,96
kN
m
.
Zgodnie z rysunkiem 5.8 ekstremalny moment zginający w przedziale AB wynosi
M
1
=
33,0⋅
3,2402,0
−
12,0⋅
4,03,240
−
1
2
⋅
12,96⋅3,240⋅
1
3
⋅
3,240=63,37 kNm
.
Zgodnie z rysunkiem 5.9 a) moment zginający z prawej strony punktu B wynosi
M
B
P
=
33,0⋅2,0−12,0⋅4,0=18,0 kNm
.
Zgodnie z rysunkiem 5.9 b) moment zginający z lewej strony punktu C wynosi
M
C
L
=−
12,0⋅2,0=−24,0 kNm
.
Zgodnie z rysunkiem 5.10 a) moment zginający z prawej strony punktu C wynosi
M
C
P
=−
12,0⋅2,0=−24,0kNm
.
Dr inż. Janusz Dębiński
BNS-I
WM
5. Ćwiczenie projektowe numer 5 – przykład 1
5
A
24,0 kN/m
6,0
[m]
51,0 kN
A
51,0 kN
M
B
(L)
a)
b)
M
A
Rys. 5.6. Momenty zginające w przedziale AB
[m]
6,0
24,0 kN/m
3,240
q
1
Rys. 5.7. Obciążenie ciągłe w ekstremum momentu zginającego
B
C
D
12,0 kN
3,240
2,0
2,0
[m]
33,0 kN
M
1
12,96 kN/m
Rys. 5.8. Ekstremalny moment zginający w przedziale AB
C
D
12,0 kN
2,0
[m]
33,0 kN
2,0
M
B
(P)
C
D
12,0 kN
2,0
[m]
33,0 kN
M
C
(L)
a)
b)
Rys. 5.9. Momenty zginające w przedziale BC
D
12,0 kN
2,0
[m]
M
C
(P)
D
12,0 kN
M
D
a)
b)
Rys. 5.10. Momenty zginające w przedziale CD
Zgodnie z rysunkiem 5.10 b) moment zginający w punkcie D wynosi
Dr inż. Janusz Dębiński
BNS-I
WM
5. Ćwiczenie projektowe numer 5 – przykład 1
6
A
B
C
D
12,0 kN
24,0 kN/m
6,0
2,0
2,0
[m]
51,0 kN
33,0 kN
T(x) [kN]
M(x) [kNm]
2,760
3,240
2,760
3,240
51
,0
21,0
12,0
0,
0
1
8,
0
24
,0
0
,0
63
,3
7
α
α
Rys. 5.11. Wykresy sił przekrojowych w belce
M
D
=
0,0 kNm
.
Rysunek 5.11 przedstawia wykres momentu zginającego w belce.
5.6. Zaprojektowanie przekroju blachownicowego belki
Zgodnie z rysunkiem 5.11 wartość ekstremalnego momentu zginającego na długości belki wynosi
M
Y
EXT
=
63,37 kNm
=
6337kNcm
.
Wytrzymałość materiału wynosi
R
=
215 MPa
=
21,5
kN
cm
2
.
Wskaźnik przekroju powinien spełniać warunek
W
Y
6337
21,5
=
294,7 cm
3
.
Dr inż. Janusz Dębiński
BNS-I
WM
5. Ćwiczenie projektowe numer 5 – przykład 1
7
[cm]
10,6
24
,0
0,87
1,
3
1
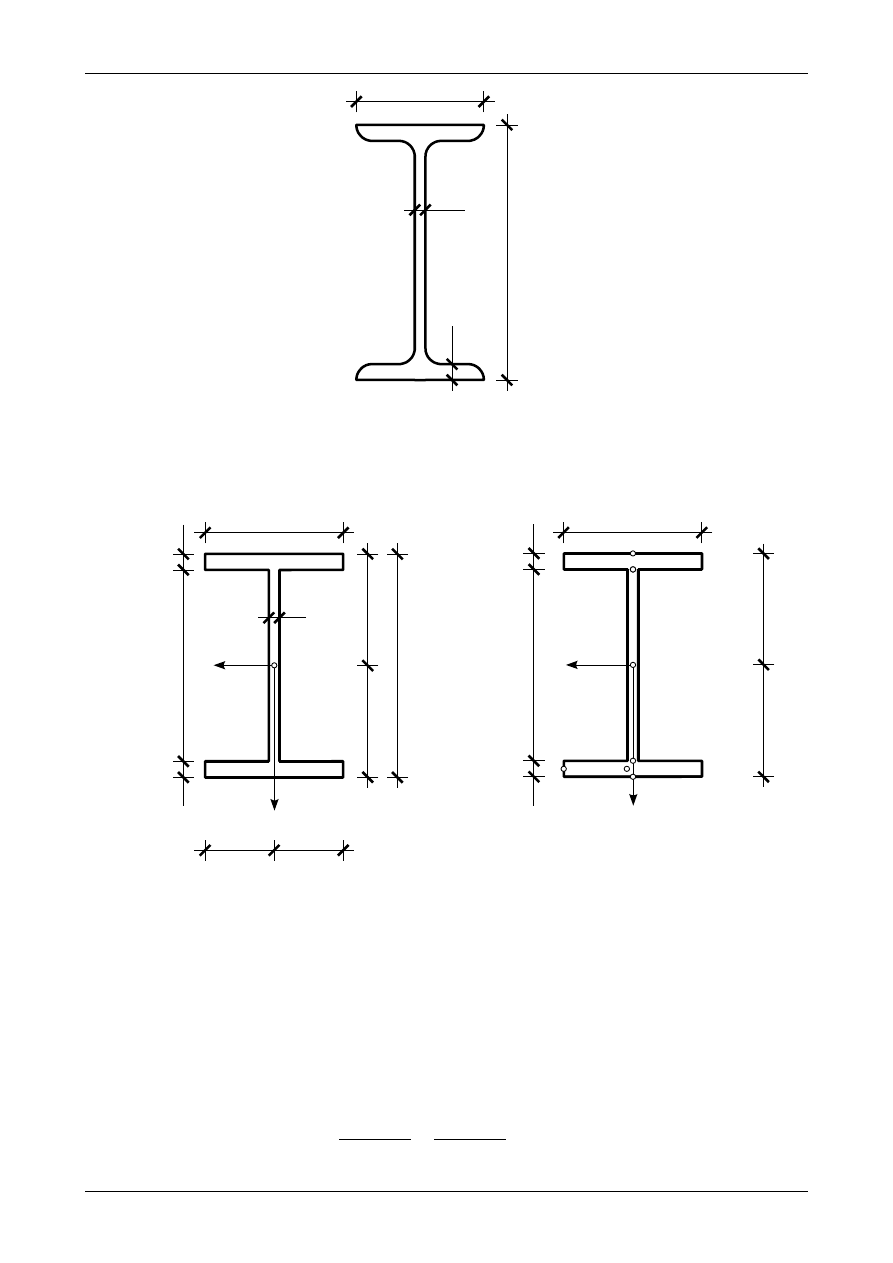
Rys. 5.12. Dwuteownik normalny 240
Y=Y
0
=Y
gl
Z=Z
0
=Z
gl
11
,9
11
,9
11,0
0,9
[cm]
5,5
5,5
2
1,
0
1
,4
1
,4
sc
2
3,
8
1
3=sc
4
5
Y=Y
0
=Y
gl
Z=Z
0
=Z
gl
21
,0
1,
4
1,
4
11,0
[cm]
6
7
2
11
,9
11
,9
a)
b)
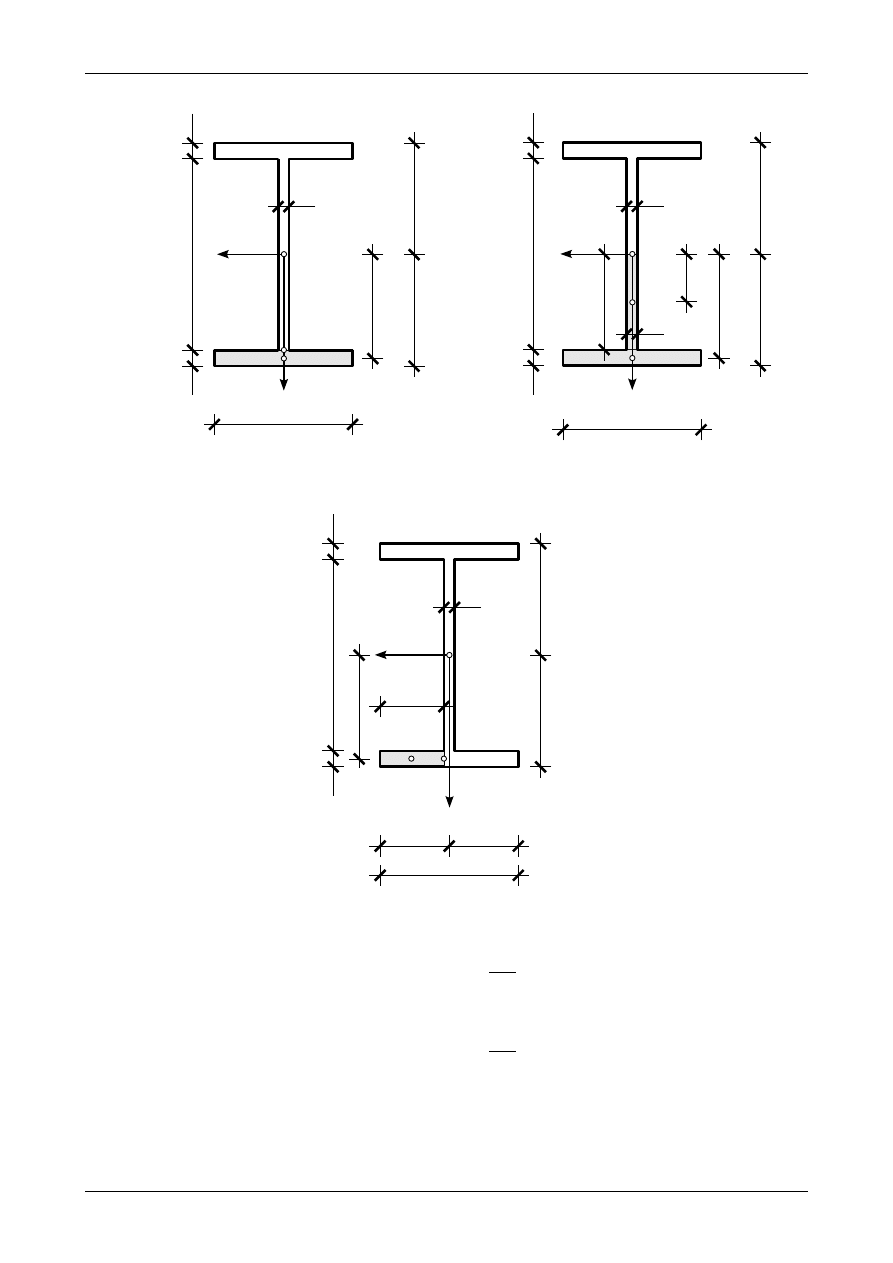
Rys. 5.13. Przekrój blachownicowy
Rysunek 5.12 przedstawia dwuteownik 240, którego wskaźnik wytrzymałości wynosi
W
Y
=
354 cm
3
.
Rysunek 5.13 przedstawia przyjęty przekrój blachownicowy. Główny moment bezwładności względem osi
Y wynosi
J
Y
=
11,0
⋅
23,8
3
12
−
10,1
⋅
21,0
3
12
=
4563cm
4
.
Dr inż. Janusz Dębiński
BNS-I
WM
5. Ćwiczenie projektowe numer 5 – przykład 1
8
24,0 kNm
2
1,
0
k
N
X
Z=Z
0
=Z
gl
Rys. 5.14. Siły przekrojowe w przekroju
α−α
Wskaźnik wytrzymałości przekroju blachownicowego wynosi
W
Y
=
4563
11,9
=
383,4 cm
3
294,7 cm
3
.
5.7. Wykresy naprężenia normalnego i stycznego w przekroju blachownicowym
Rysunek 5.14 przedstawia wartości i zwroty siły poprzecznej i momentu zginającego działające
w przekroju
α
-
α
odczytane na podstawie rysunku 5.11. Wartość bezwzględna siły poprzecznej wynosi
∣
T
Z
∣
=
21,0 kN
.
Wartość momentu zginającego wynosi
M
Y
=−
24,0 kNm
=−
2400 kNcm
.
Funkcja naprężenia normalnego ma postać
X
=
−
2400
4563
⋅
z
=−
0,5260
⋅
z
.
Zgodnie z oznaczeniami na rysunku 5.13 b) naprężenia normalne w punktach od 1 do 5 wynoszą
X
1
=−
0,5260⋅11,9=−6,259
kN
cm
2
=−
62,59 MPa
,
X
2
=−
0,5260⋅10,5=−5,523
kN
cm
2
=−
55,23 MPa
,
X
3
=−
0,5260⋅0,0=0,0
kN
cm
2
=
0,0 MPa
,
Dr inż. Janusz Dębiński
BNS-I
WM
5. Ćwiczenie projektowe numer 5 – przykład 1
9
Y=Y
0
=Y
gl
Z=Z
0
=Z
gl
11
,2
11,0
0,9
[cm]
21
,0
1,
4
1,
4
11
,9
11
,9
Y=Y
0
=Y
gl
Z=Z
0
=Z
gl
11
,2
11,0
0,9
[cm]
21
,0
1,
4
1,
4
11
,9
11
,9
5,
2
5
0,9
1
0,
5
2
sc
1
3=sc
sc
2
sc
1
sc
a)
b)
Rys. 5.15. Części przekroju do wyznaczenia naprężeń stycznych
τ
XZ
Y=Y
0
=Y
gl
Z=Z
0
=Z
gl
11
,2
11,0
0,9
[cm]
5,5
5,5
2
1,
0
1
,4
1
,4
5,05
6
11
,9
11
,9
sc
3
sc
Rys. 5.16. Część przekroju do wyznaczenia naprężenia stycznego
τ
XY
X
4
=−
0,5260⋅
−
10,5
=
5,523
kN
cm
2
=
55,23 MPa
,
X
5
=−
0,5260⋅
−
11,9
=
6,259
kN
cm
2
=
62,59 MPa
.
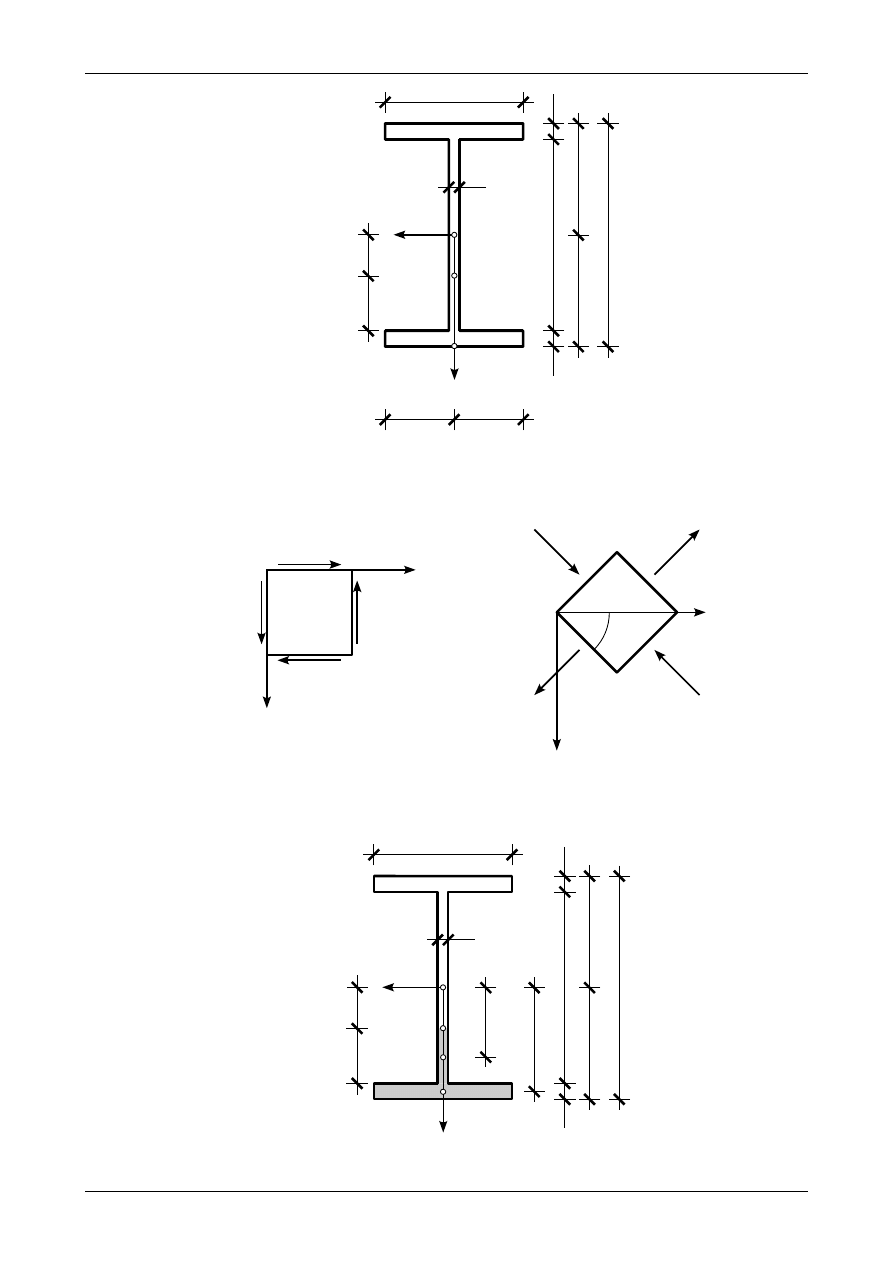
Rysunek 5.17 przedstawia wykres naprężenia normalnego na wysokości przekroju blachownicowego.
Naprężenie styczne
τ
XZ
w punkcie 1 wynosi zero. Wartość bezwzględna naprężenia stycznego
τ
XZ
w punkcie
2 znajdującym się w półce, zgodnie z rysunkiem 5.15 a) wynosi
Dr inż. Janusz Dębiński
BNS-I
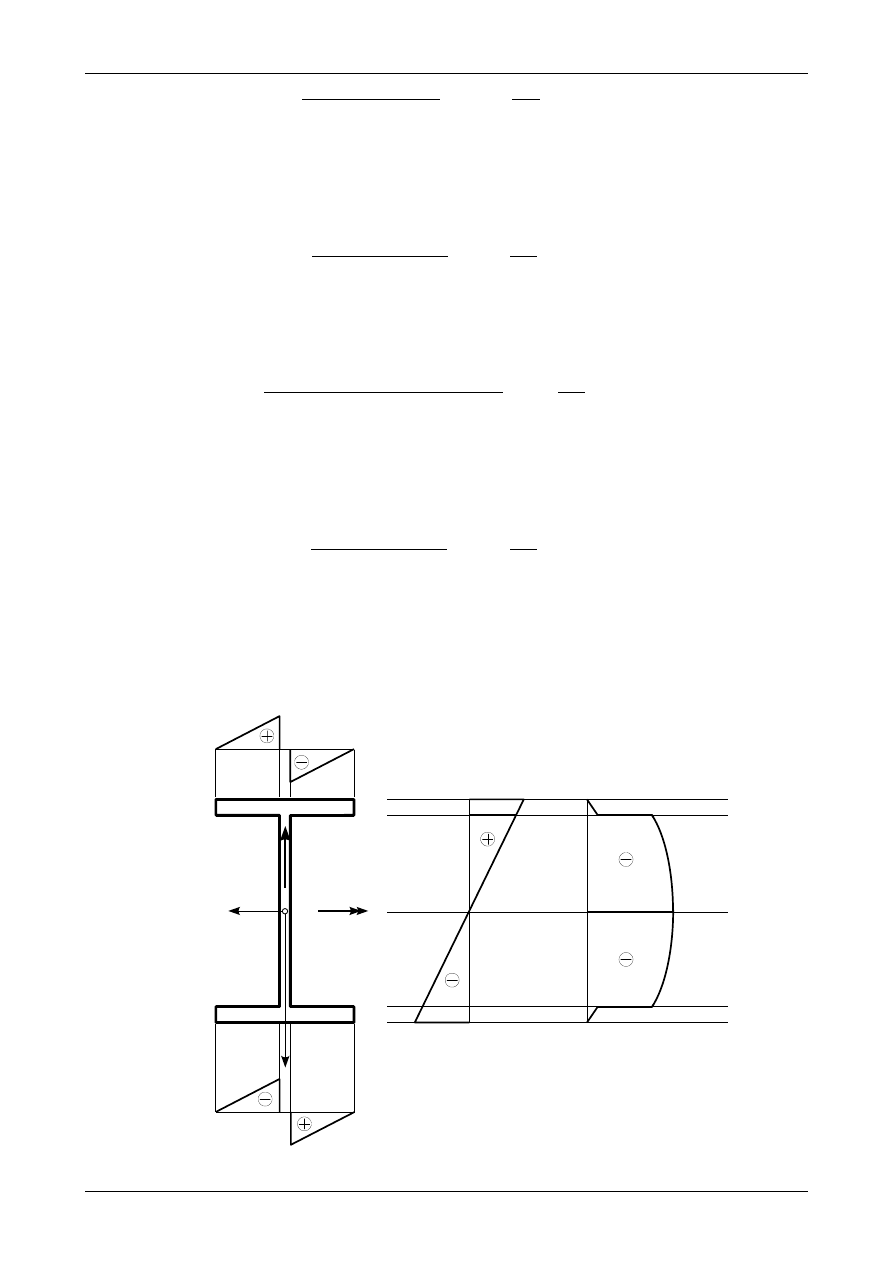
WM
5. Ćwiczenie projektowe numer 5 – przykład 1
10
∣
XZ
2p
∣
=
21,0⋅
11,0⋅1,4⋅11,2
11,0⋅4563
=
0,07216
kN
cm
2
=
0,7216 MPa
.
Wartość bezwzględna naprężenia stycznego
τ
XZ
w punkcie 2 znajdującym się w środniku, zgodnie z rysun-
kiem 5.15 a) wynosi
∣
XZ
2s
∣
=
21,0⋅
11,0⋅1,4⋅11,2
0,9⋅4563
=
0,8820
kN
cm
2
=
8,820 MPa
.
Zgodnie z rysunkiem 5.15 b) wartość bezwzględna naprężenia stycznego w punkcie 3 wynosi
∣
XZ
3
∣
=
21,0⋅
11,0⋅1,4⋅11,210,5⋅0,9⋅5,25
0,9⋅4563
=
1,136
kN
cm
2
=
11,36 MPa
.
Rysunek 5.17 przedstawia wykres naprężenia stycznego
τ
XZ
na wysokości przekroju blachownicowego.
Naprężenia te są ujemne w układzie ZX. Zgodnie z rysunkiem 5.16 naprężenie styczne w punkcie 6 wynosi
∣
XY
6
∣
=
21,0⋅
5,05⋅1,4⋅11,2
1,4⋅4563
=
0,2603
kN
cm
2
=
2,603 MPa
.
Rysunek 5.17 przedstawia wykres naprężenia stycznego
τ
XY
w półkach przekroju blachownicowego.
Y=Y
0
=Y
gl
Z=Z
0
=Z
gl
24,0 kNm
21,0 kN
N=0,0 kN
[MPa]
62,59
55,23
55,23
62,59
0,0
0,0
0,0
[MPa]
0,7216
8,820
8,820
11,36
[MPa]
2,
60
3
0
,0
0,
0
[MPa]
0
,0
0,
0
σ
X
τ
XZ
τ
XY
τ
XY
sc
0,7216
2,
60
3
2,
60
3
2
,6
03
Rys. 5.17. Wykresy naprężeń w przekroju blachownicowym
Dr inż. Janusz Dębiński
BNS-I
WM
5. Ćwiczenie projektowe numer 5 – przykład 1
11
Y=Y
0
=Y
gl
Z=Z
0
=Z
gl
11
,9
11
,9
11,0
0,9
[cm]
5,5
5,5
21
,0
1,
4
1,
4
A=sc
23
,8
B
C
0,3∙21,0=6,3
4,2
Rys. 5.18. Przekrój blachownicowy
X
Z
11,36 MPa
11,36 MPa
a)
11
,3
6
M
Pa
11
,36
M
Pa
11
,3
6
M
Pa
11
,36
M
Pa
X
Z
b)
45
0
Rys. 5.19. Graficzna interpretacja stanu naprężenia w punkcie A
Y=Y
0
=Y
gl
Z=Z
0
=Z
gl
11
,9
11
,9
11,0
0,9
[cm]
21
,0
1,
4
1,
4
sc
23
,8
B
0,3∙21,0=6,3
4,2
11
,2
7
,3
5
sc
1
sc
2
Rys. 5.20. Części przekroju do wyznaczenia naprężenia stycznego
τ
XZ
Dr inż. Janusz Dębiński
BNS-I
WM
5. Ćwiczenie projektowe numer 5 – przykład 1
12
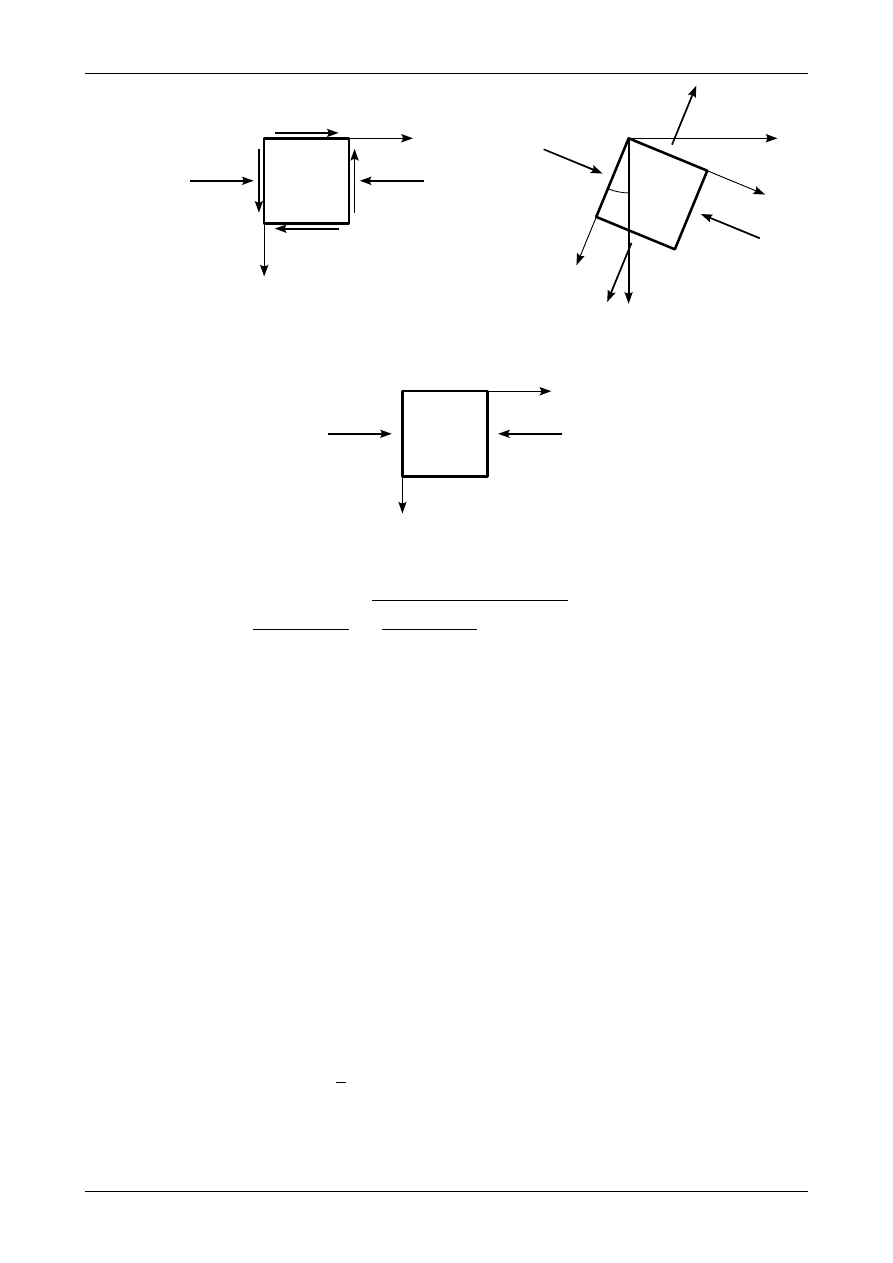
5.8. Naprężenia główne w punktach A, B i C
Rysunek 5.18 przedstawia przekrój blachownicowy z zaznaczonymi punktami A, B i C. W punkcie A
występuje czyste ścinanie. Rysunek 5.19 a) przedstawia ten stan naprężenia w układzie ZX natomiast
rysunek 5.19 b) przedstawia naprężenia i kierunek główny. W punkcie B naprężenie normalne wynosi
X
B
=−
0,5260⋅4,2=−2,209
kN
cm
2
=−
22,09 MPa
.
Zgodnie z rysunkiem 5.20 wartość bezwzględna naprężenia stycznego w punkcie B wynosi
∣
XZ
B
∣
=
21,0⋅
11,0⋅1,4⋅11,26,3⋅0,9⋅7,35
0,9⋅4563
=
1,095
kN
cm
2
=
10,95 MPa
.
Naprężenie to jest w układzie ZX ujemne czyli wynosi
XZ
B
=−
10,95 MPa
.
Tensor naprężenia ma postać
=
[
−
22,09 0
−
10,95
0
0
0
−
10,95 0
0
]
[
MPa
]
.
Rysunek 5.21 a) przedstawia graficzną interpretację tego stanu naprężenia. Kąt nachylenia osi głównych
wynosi
tg
2⋅
gl
=
2⋅
−
10,95
0,0−
−
22,09
=−
0,9914
.
Kąt nachylenia osi głównych wynosi
gl
=−
22,38 °
.
Naprężenia główne wynoszą więc
Zgl
=
0,0
−
22,09
2
0,0−
−
22,09
2
⋅
cos
2⋅
−
22,38°
−
10,95⋅sin
2⋅
−
22,38°
=
4,508 MPa
,
Xgl
=
0,0
−
22,09
2
−
0,0−
−
22,09
2
⋅
cos
2⋅
−
22,38°
−
−
10,95
⋅
sin
2⋅
−
22,09 °
=−
26,60 MPa
.
Dr inż. Janusz Dębiński
BNS-I
WM
5. Ćwiczenie projektowe numer 5 – przykład 1
13
X
Z
22,09 MPa
22,09 MPa
10,95 MPa
10,95 MPa
26,60
MPa
26,60
MPa
4,508
MPa
4,508
MPa
X
Z
Z
gl
X
gl
22,38
0
b)
a)
Rys. 5.21. Graficzna interpretacja stanu naprężenia w punkcie B
X=X
gl
Z=Z
gl
62,59 MPa
62,59 MPa
Rys. 5.22. Graficzna interpretacja stanu naprężenia w punkcie C
1/2
=
0,0
−
22,09
2
±
0,0−
−
22,09
2
2
−
10,95
2
=
{
4,508 MPa
−
26,60 MPa
.
Niezmienniki stanu naprężenia wynoszą
I
1
=
0,0
−
22,09
=−
22,09 MPa
,
I
1
=
4,508
−
26,60
=−
22,09 MPa
,
I
2
=
0,0⋅
−
22,09
−
−
10,95
2
=−
119,9 MPa
2
,
I
2
=
−
26,60
⋅
4,508=−119,9 MPa
2
.
Rysunek 5.21 b) przedstawia naprężenia główne w punkcie B. Tensor naprężenia ma postać
gl
=
[
−
26,60 0
0
0
0
0
0
0 4,508
]
[
MPa
]
.
Rysunek 5.22 przedstawia graficzną interpretację stanu naprężenia w punkcie C. Przedstawia on także
naprężenia i kierunek główny.
Dr inż. Janusz Dębiński
BNS-I
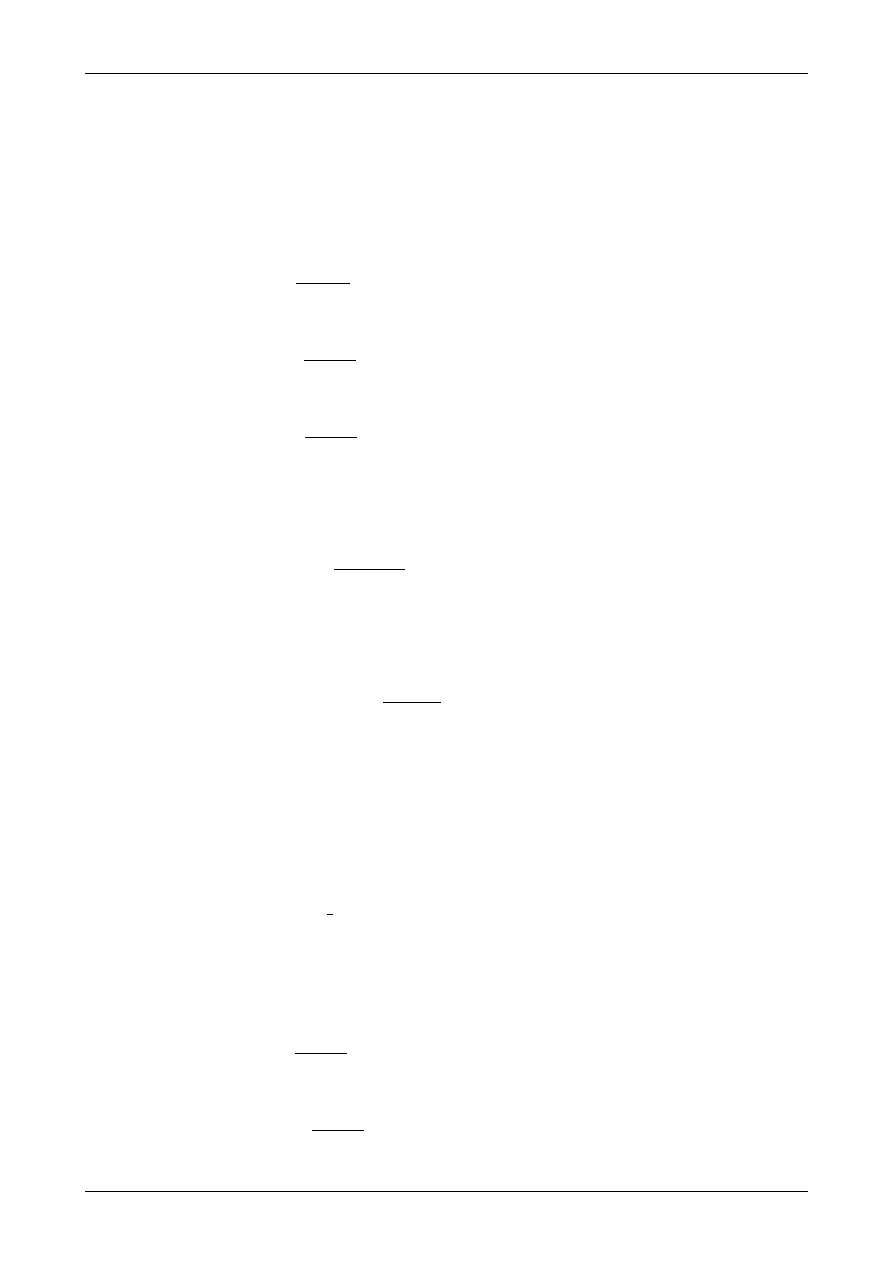
WM
5. Ćwiczenie projektowe numer 5 – przykład 1
14
5.9. Stan odkształcenia oraz naprężenia zredukowane w punkcie B
Belka wykonana jest ze stali budowlanej St3S. Wartość modułu Younga. Dla tego gatunku stali
wynosi
E
=
205GPa
=
205000 MPa
.
Odkształcenia liniowe w układzie ZX wynoszą
X
=
1
205000
⋅
[
−
22,09−0,3⋅
0,00,0
]
=−
107,8⋅10
−
6
,
Y
=
1
205000
⋅
[
0,0−0,3⋅
−
22,090,0
]
=
32,33⋅10
−
6
,
Z
=
1
205000
⋅
[
0,0−0,3⋅
−
22,090,0
]
=
32,33⋅10
−
6
.
Moduł Kirchhoffa wynosi
G
=
205
2
⋅
1
0,3
=
78,85 GPa
=
78850 MPa
.
Odkształcenia postaciowe wynoszą
XZ
=
−
10,95
2
⋅
78850
=−
69,44
⋅
10
−
6
,
XY
=
YZ
=
0
.
Tensor odkształcenia ma postać
=
[
−
107,8
0
−
69,44
0
32,33
0
−
69,44
0
32,33
]
⋅
10
−
6
.
Odkształcenia główne wynoszą
Xgl
=
1
205000
⋅
[
−
26,60−0,3⋅
4,5080,0
]
=−
136,4⋅10
−
6
,
Ygl
=
1
205000
⋅
[
0−0,3⋅
4,508−26,60
]
=
32,33⋅10
−
6
,
Dr inż. Janusz Dębiński
BNS-I
WM
5. Ćwiczenie projektowe numer 5 – przykład 1
15
Zgl
=
1
205000
⋅
[
4,508−0,3⋅
−
26,600,0
]
=
60,92⋅10
−
6
Tensor odkształcenia w układzie osi głównych ma postać
gl
=
[
−
136,4
0
0
0
32,33
0
0
0
60,92
]
⋅
10
−
6
.
Naprężenie zredukowane według hipotezy H-M-H wynosi
red
H
−
M
−
H
=
−
22,09
2
3
⋅
−
10,95
2
=
29,11 MPa
.
Naprężenie zredukowane według hipotezy Treski wynosi
red
T
=
−
22,09
2
4⋅
−
10,95
2
=
31,11 MPa
.
Dr inż. Janusz Dębiński
BNS-I
Document Outline