PROGRAM 1.2.

Obliczanie pierwiastka kwadratowego.

Przedstawianie w postaci ułamka łańcuchowego.

Pierwiastek(m) - m = 7

Dokładność obliczeń - eps = 1.0E-0010

Wartość pierwiastka: 2.645751311E+0000

Błąd pierwiastka: 4.44E-0012

Liczba ogniw ułamka: 20

1.6. Rozwijanie funkcji w ułamki łańcuchowe

Ułamki łańcuchowe stanowią wygodny aparat do przedstawiania i obliczania wartości funkcji.

Aby rozwinąć daną funkcję w ułamek łańcuchowy musimy najpierw przed-stawić ją w postaci funkcji wymiernej

(1.20)

Przy wykorzystaniu wzoru (1.20) rozpatrzymy obliczanie wartości wielomianu

(1.21)

przyjmując funkcje i również w postaci wielomianów

(1.22)

Po przyrównaniu prawych stron (1.21) i (1.22) otrzymujemy zależność

z której wynika układ równań dla określenia nieznanych współczynników

(1.23)

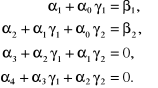
(1.23d.)

Błąd aproksymacji wielomianu (1.21) funkcją wymierną (1.22) - (1.23) można ocenić za pomocą współczynnika wielomianu

(1.24)

Rozważmy w charakterze przykładu rozwinięcie funkcji w szereg Maclaurina

(1.25)

zbieżny dla . Dla tej funkcji, po rozwiązaniu układu równań (1.23), otrzymujemy:

i następnie mamy

(1.26)

przy czym błąd aproksymacji (1.24) szeregu Maclaurina zawierającego wyrazy do włącznie funkcją wymierną (1.26) wynosi

Rozwinięcie funkcji wymiernej

(1.27)

w ułamek łańcuchowy jest realizowane poprzez wykonywanie kolejnych przekształceń elementarnych

,

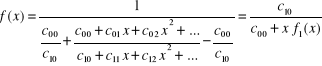
gdzie

oraz

W taki sam sposób rozkładamy funkcję

gdzie

przy czym

itd.

Współczynniki określające rozwinięcie funkcji (1.27) w ułamek łańcuchowy

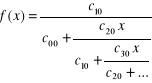
najwygodniej jest obliczać z ogólnego wzoru

dla

Wykorzystując opisany algorytm łatwo uzyskujemy rozwinięcie rozważanej funkcji (1.26) w ułamek łańcuchowy

(1.28)

Pełne rozwinięcie funkcji w ułamek łańcuchowy (1.28) jest następujące [2]:

(1.29)

Rozwinięcie to jest osobliwe dla ponieważ jest

liczbę należy więc obliczać jako kwadrat liczby e.

{Program 1.3}

unit Obliczenia;

interface

uses

Windows, Messages, SysUtils, Classes, Graphics, Controls,

Forms, Dialogs, StdCtrls, Buttons, OleCtnrs;

. . . . . . . . . . . . . . . . . . . . . .

var

Form3: TForm3;

i,j,k,n: Integer;

bl,c,dx,eps,sum,sump,x,xmax: Double;

a,b: array [0..20] of Real;

nap,zbior: String;

plik: Text;

implementation

uses Ustawienia, Informacje, Grafika, Podglad;

. . . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn1Click(Sender: TObject);

begin

Form2.Show;

Form2.Wyniki.Lines.Text:='';

zbior:=Edit4.Text;

AssignFile(plik,zbior); Rewrite(plik);

if RadioButton1.Checked then nap:=' Exp(x)' else nap:='Tan(th)';

Writeln(plik,'PROGRAM 1.3.');

Writeln(plik,'Obliczanie wartości funkcji ',nap,'.');

Writeln(plik,'Metoda rozwijania w ułamki łańcuchowe.');

n:=StrToInt(Edit2.Text);

Write(plik,'n = ',n:3);

if RadioButton1.Checked then begin

label2.Caption:='Prawy koniec przedziału - xmax = ';

xmax:=StrToFloat(Edit3.Text);

end

else begin

label2.Caption:='Prawy koniec przedziału - thmax = ';

xmax:=StrToFloat(Edit3.Text);

end;

if RadioButton1.Checked then

Write(plik,', xmax = ',xmax:13)

else

Write(plik,', thmax = ',xmax:13);

eps:=StrToFloat(Edit1.Text);

Writeln(plik,', eps = ',eps:9);

Writeln(plik,'');

if RadioButton1.Checked then

Writeln(plik,' i x ',nap,'

błąd k')

else

Writeln(plik,' i th ',nap,'

błąd k');

if RadioButton2.Checked then xmax:=xmax*Pi/180;

dx:=xmax/n; a[0]:=0; b[0]:=0;

for i:=1 to n do begin

x:=i*dx;

if RadioButton1.Checked then begin

a[1]:=1; a[2]:=2+x;

b[1]:=1; b[2]:=-2*x;

for j:=3 to 20 do begin

a[j]:=4*(j-2)+2;

b[j]:=x*x;

end;

end;

if RadioButton2.Checked then begin

for j:=1 to 20 do begin

a[j]:=2*(j-1)+1;

b[j]:=-x*x;

end;

b[1]:=x;

end;

k:=1; sump:=0;

repeat

c:=b[k]/a[k];

for j:=1 to k do begin

sum:=a[k-j]+c;

c:=b[k-j]/sum;

end;

bl:=Abs(sum-sump);

k:=k+1; sump:=sum;

until bl<eps;

if RadioButton1.Checked then bl:=Abs(sum-Exp(x))

else bl:=Abs(sum-Sin(x)/Cos(x));

if RadioButton2.Checked then x:=x*180/Pi;

Writeln(plik,i:3,' ',x:6:3,' ',sum:18,' ',bl:11,' ',k:2);

end;

CloseFile(plik);

Form2.Wyniki.Lines.LoadFromFile(zbior);

end;

. . . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn3Click(Sender: TObject);

begin

Close;

end;

end.

W programie 1.3 wyznaczane są z zadaną dokładnością wartości funkcji oraz z rozwinięcia (1.29) oraz rozwinięcia w ułamek łańcuchowy [2]

w przedziałach i w n równoodległych punktach.

Uzyskane wyniki porównano z rezultatami wywołań odpowiednich arytmetycznych funkcji standardowych. Drukowana jest także liczba ogniw k ułamka łańcuchowego, niezbędna do obliczenia wartości funkcji z zadaną dokładnością Wykonane przez program 1.3 obliczenia wartości funkcji i zawierają dwa kolejne tabulogramy wyników.

PROGRAM 1.3.

Obliczanie wartości funkcji Exp(x).

Metoda rozwijania w ułamki łańcuchowe.

n = 30, xmax = 1.5000E+0000, eps = 1.0E-0008

i x Exp(x) błąd k

1 0.050 1.051271096E+0000 3.96E-0014 5

2 0.100 1.105170918E+0000 1.06E-0013 6

3 0.150 1.161834243E+0000 1.50E-0014 6

4 0.200 1.221402758E+0000 5.28E-0014 6

5 0.250 1.284025417E+0000 1.93E-0013 6

6 0.300 1.349858808E+0000 6.15E-0013 6

7 0.350 1.419067549E+0000 4.21E-0012 6

8 0.400 1.491824698E+0000 2.71E-0013 7

9 0.450 1.568312185E+0000 6.03E-0013 7

10 0.500 1.648721271E+0000 8.02E-0014 7

11 0.550 1.733253018E+0000 1.03E-0012 7

12 0.600 1.822118800E+0000 2.38E-0012 7

13 0.650 1.915540829E+0000 2.50E-0013 7

14 0.700 2.013752707E+0000 2.97E-0012 7

15 0.750 2.117000017E+0000 9.01E-0012 7

16 0.800 2.225540928E+0000 1.23E-0012 8

17 0.850 2.339646852E+0000 2.85E-0012 8

18 0.900 2.459603111E+0000 3.36E-0012 8

19 0.950 2.585709659E+0000 2.01E-0012 8

20 1.000 2.718281828E+0000 4.82E-0013 8

21 1.050 2.857651118E+0000 3.67E-0012 8

22 1.100 3.004166024E+0000 3.06E-0012 8

23 1.150 3.158192910E+0000 8.64E-0012 8

24 1.200 3.320116923E+0000 3.49E-0012 8

25 1.250 3.490342957E+0000 1.13E-0011 8

26 1.300 3.669296668E+0000 2.37E-0011 8

27 1.350 3.857425531E+0000 7.35E-0012 9

28 1.400 4.055199967E+0000 7.47E-0012 9

29 1.450 4.263114515E+0000 4.07E-0012 9

30 1.500 4.481689070E+0000 4.54E-0013 9

PROGRAM 1.3.

Obliczanie wartości funkcji Tan(th).

Metoda rozwijania w ułamki łańcuchowe.

n = 89, thmax = 8.9000E+0001, eps = 1.0E-0008

i th Tan(th) błąd k

1 1.000 1.745506493E-0002 2.15E-0015 4

2 2.000 3.492076949E-0002 3.52E-0014 4

3 3.000 5.240777928E-0002 7.08E-0013 4

4 4.000 6.992681194E-0002 9.49E-0015 5

5 5.000 8.748866353E-0002 1.90E-0014 5

6 6.000 1.051042352E-0001 5.77E-0014 5

7 7.000 1.227845609E-0001 1.57E-0014 5

8 8.000 1.405408347E-0001 1.87E-0013 5

9 9.000 1.583844403E-0001 4.91E-0013 5

10 10.000 1.763269807E-0001 1.58E-0012 5

11 11.000 1.943803091E-0001 3.63E-0012 5

12 12.000 2.125565617E-0001 8.94E-0014 6

13 13.000 2.308681911E-0001 3.08E-0015 6

14 14.000 2.493280028E-0001 7.57E-0014 6

15 15.000 2.679491924E-0001 1.35E-0013 6

16 16.000 2.867453858E-0001 4.75E-0014 6

17 17.000 3.057306815E-0001 2.73E-0013 6

18 18.000 3.249196962E-0001 1.02E-0013 6

19 19.000 3.443276133E-0001 5.23E-0013 6

20 20.000 3.639702343E-0001 1.12E-0012 6

21 21.000 3.838640350E-0001 2.05E-0012 6

22 22.000 4.040262258E-0001 3.01E-0012 6

23 23.000 4.244748162E-0001 5.20E-0012 6

24 24.000 4.452286853E-0001 8.54E-0012 6

25 25.000 4.663076581E-0001 1.31E-0011 6

26 26.000 4.877325885E-0001 2.07E-0011 6

27 27.000 5.095254495E-0001 2.02E-0013 7

28 28.000 5.317094317E-0001 1.39E-0013 7

29 29.000 5.543090515E-0001 1.04E-0013 7

30 30.000 5.773502692E-0001 1.39E-0013 7

31 31.000 6.008606190E-0001 5.94E-0013 7

32 32.000 6.248693519E-0001 4.08E-0013 7

33 33.000 6.494075932E-0001 3.37E-0013 7

34 34.000 6.745085168E-0001 1.33E-0012 7

35 35.000 7.002075382E-0001 1.51E-0012 7

36 36.000 7.265425280E-0001 1.98E-0012 7

37 37.000 7.535540501E-0001 3.89E-0012 7

38 38.000 7.812856265E-0001 5.15E-0012 7

39 39.000 8.097840332E-0001 8.20E-0012 7

40 40.000 8.390996312E-0001 1.10E-0011 7

41 41.000 8.692867378E-0001 1.53E-0011 7

42 42.000 9.004040443E-0001 2.22E-0011 7

43 43.000 9.325150861E-0001 3.08E-0011 7

44 44.000 9.656887748E-0001 7.55E-0014 8

45 45.000 1.000000000E+0000 7.38E-0013 8

46 46.000 1.035530314E+0000 4.92E-0013 8

47 47.000 1.072368710E+0000 1.18E-0013 8

48 48.000 1.110612515E+0000 1.04E-0012 8

49 49.000 1.150368407E+0000 6.66E-0013 8

50 50.000 1.191753593E+0000 4.24E-0013 8

51 51.000 1.234897157E+0000 2.21E-0012 8

52 52.000 1.279941632E+0000 1.83E-0012 8

53 53.000 1.327044822E+0000 2.36E-0012 8

54 54.000 1.376381920E+0000 4.63E-0012 8

55 55.000 1.428148007E+0000 5.42E-0012 8

56 56.000 1.482560969E+0000 6.83E-0012 8

57 57.000 1.539864964E+0000 1.13E-0011 8

58 58.000 1.600334529E+0000 1.48E-0011 8

59 59.000 1.664279482E+0000 2.13E-0011 8

60 60.000 1.732050808E+0000 2.69E-0011 8

61 61.000 1.804047755E+0000 3.60E-0011 8

62 62.000 1.880726465E+0000 5.10E-0011 8

63 63.000 1.962610506E+0000 2.49E-0013 9

64 64.000 2.050303842E+0000 1.40E-0013 9

65 65.000 2.144506921E+0000 1.56E-0013 9

66 66.000 2.246036774E+0000 2.96E-0014 9

67 67.000 2.355852366E+0000 6.27E-0013 9

68 68.000 2.475086853E+0000 1.57E-0012 9

69 69.000 2.605089065E+0000 9.50E-0013 9

70 70.000 2.747477419E+0000 9.39E-0013 9

71 71.000 2.904210878E+0000 3.67E-0012 9

72 72.000 3.077683537E+0000 3.10E-0012 9

73 73.000 3.270852618E+0000 8.36E-0012 9

74 74.000 3.487414444E+0000 1.58E-0011 9

75 75.000 3.732050808E+0000 1.27E-0011 9

76 76.000 4.010780934E+0000 2.61E-0011 9

77 77.000 4.331475874E+0000 3.44E-0011 9

78 78.000 4.704630109E+0000 6.09E-0011 9

79 79.000 5.144554016E+0000 3.90E-0012 10

80 80.000 5.671281820E+0000 6.75E-0012 10

81 81.000 6.313751515E+0000 1.38E-0011 10

82 82.000 7.115369722E+0000 8.42E-0012 10

83 83.000 8.144346428E+0000 1.47E-0011 10

84 84.000 9.514364454E+0000 2.47E-0011 10

85 85.000 1.143005230E+0001 3.37E-0011 10

86 86.000 1.430066625E+0001 1.02E-0010 10

87 87.000 1.908113669E+0001 2.60E-0010 10

88 88.000 2.863625328E+0001 1.70E-0010 11

89 89.000 5.728996163E+0001 1.58E-0009 11

1.7. Sumowanie szeregów potęgowych

Rozwijanie funkcji w szeregi potęgowe okazuje się w wielu przypadkach wygodnym sposobem obliczania ich wartości. Zakładając, że funkcja
jest ciągła i ma dostateczną liczbę pochodnych w otoczeniu punktu możemy przybliżyć ją szeregiem potęgowym Taylora

(1.30)

lub też dla ξ = 0 szeregiem potęgowym Maclaurina

(1.31)

Błąd obcięcia szeregów (1.30) i (1.31) jest równy reszcie szeregu Taylora

(1.32)

lub reszcie szeregu Maclaurina

(1.33)

dla przyjmujących wartości z przedziału:

Najtrudniej jest określić zbieżność szeregów (1.30) - (1.31) poprzez badanie ich reszt (1.32) - (1.33), zwykle wyznacza się więc ich promienie zbieżności.

26 1. Wprowadzenie do metod numerycznych

1.6. Rozwijanie funkcji w ułamki łańcuchowe 29

---