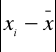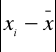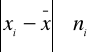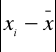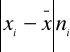ANALIZA STATYSTYCZNA

Badanie statystyczne nie kończy się na opracowaniu tablic statystycznych, czy wykresów.

Ostatecznym celem każdego badania z zakresu statystyki jest analiza statystyczna danych wynikowych i wyciągnięcie na jej podstawie wniosków dotyczących :

• wielkości badanego zjawiska .

• jego poziomu przeciętnego.

• prawidłowości i zależności zachodzących w badanej zbiorowości.

• kierunków rozwojowych.

Podstawowym zadaniem analizy statystycznej jest wykrycie prawidłowości zachodzących w badanej zbiorowości, ich bliższe poznanie, zachowanie w określonych warunkach oraz interpretacja istoty tych prawidłowości.

Rzetelna analiza, kończąca się wyciągnięciem wniosków jest podstawą optymalnych decyzji podejmowanych na różnych szczeblach zarządzania.

Do wykrycia i uchwycenia prawidłowości w badanej zbiorowości dochodzi się poprzez porównywanie ze sobą szeregów statystycznych oraz poszczególnych pozycji tych szeregów.

W pracach analitycznych wykorzystywane są odpowiednie miary statystyczne.

Miary statystyczne są to charakterystyki liczbowe szeregów statystycznych.

Miary statystyczne mają na ich uchwycenie i przeanalizowanie istotnych procesów, których odbiciem są te szeregi.

Każda miara statystyczna charakteryzuje badane zjawisko z określonego punktu widzenia i dlatego do wszechstronnej analizy jest konieczne stosowanie wielu różnych miar.

Do najczęściej spotykanych miar zaliczamy:

1. wskaźniki struktury

2. wskaźniki natężenia

3. wskaźniki przeciętnego poziomu (tendencji centralnej)

• średnie klasyczne

• średnie pozycyjne

4. wskaźniki dynamiki

5. miary rozproszenia

W analizie statystycznej wykorzystuje się liczby absolutne (bezwzględne) i liczby stosunkowe (względne).

Liczby absolutne - są to liczby, które uzyskujemy w wyniku zbierania informacji w badaniu statystycznym poprzez zliczenie poszczególnych jednostek lub przez sumowanie wartości cech mierzalnych.

Liczby absolutne są liczbami mianowanymi. (określają wielkość zjawiska w konkretnej jednostce miary np. waga w kg, wiek w latach)

Czasami tylko takie dane tj. liczby absolutne nie wystarczają do celów analizy statystycznej.

Dopiero porównywanie wielkości absolutnej jednego zjawiska z wielkością absolutną innego zjawiska umożliwia bardziej prawidłową ocenę badanego zjawiska.

Liczby względne: są to ilorazy wielkości zjawiska badanego przez wielkość zjawiska z nim związanego.

Liczby względne wskazują na zależności, relacje, stosunki między dwoma liczbami absolutnymi.

Do najczęściej stosowanych liczb względnych zaliczamy:

• współczynniki natężenia

• wskaźniki struktury

• indeksy.

ANALIZA STATYSTYCZNA NATĘŻENIA

W wielu przypadkach ocena zjawisk na podstawie liczb absolutnych jest bardzo trudna, a często nawet niemożliwa, np. trudno ocenić stopień nasycenia gospodarstw domowych samochodami tylko po liczbie samochodów. Dopiero gdy ustali się na ile gospodarstw przypada 1 samochód, można będzie ocenić stopień nasycenia. A więc należy ustalić wzajemny stosunek między liczbą gospodarstw i liczbą samochodów.

Przez natężenie rozumie się stosunek zbiorowości pozostających we wzajemnym związku logicznym.

Współczynniki natężenia określają liczbowo stosunek dwóch zbiorowości.

Natężeniem jest np. liczba lekarzy przypadająca na liczbę chorych, liczba pielęgniarek przypadająca na liczbę chorych, liczba widzów przypadająca na 1 seans filmowy u danego reżysera, liczba przyjęć do pracy do liczby zwolnień, itp.

Natężenie możemy określić wzorem:

Z_{1 /} Z₂

Z₁ = wielkość pierwszej zbiorowości

Z₂ = wielkość drugiej zbiorowości

Wskaźniki te, zwane współczynnikami obrazują stopień natężenia zjawiska jednej zbiorowości przypadającego na określoną jednostkę drugiej zbiorowości (np. gęstość zaludnienia na 1 km 2)

Wskaźniki natężenia pozwalają na porównywanie ze sobą wielkości, które ujmowane w liczbach bezwzględnych nie pozwalają na wyciągnięcie głębszych wniosków.

Bezrobocie w wybranych krajach

Kraj	Bezrobotni w tys. Osób	Bezrobocie w % Ogółu zatrudnionych i bezrobotnych	Bezrobotni na 1 wolne miejsce pracy
Belgia	229	8,6	55,7
Dania	107	10,0	56,3
Finlandia	90	4,0	8,0
Japonia	1080	2,0	3,1
Kanada	736	7,2	16,0
Niemcy	1060	4,6	4,5
USA	7288	7,7	.

Liczby bezwzględne bezrobotnych nie pozwalają na uściślenie wniosków o nasileniu bezrobocia m.in. ze względu na różnice w ogólnej liczbie ludności w poszczególnych krajach oraz w liczbie zatrudnionych.

Dopiero głębsza analiza wielkości pozostających w związku z bezrobociem pozwala na właściwą interpretację zjawiska (w liczbach bezwzględnych największe bezrobocie w USA, a wykorzystując wsk. natężenia w Danii największy odsetek bezrobotnych i tam najwięcej bezrobotnych przypadających na 1 wolne miejsce pracy.

ANALIZA STRUKTURY

Przez analizę struktury rozumie się badanie wewnętrznej budowy zbiorowości.

W rezultacie tego badania ustala się elementy, z których ona się składa i określa, jaką część stanowią poszczególne elementy w całości danej zbiorowości.

Analiza struktury polega na określeniu i zinterpretowaniu prawidłowości występujących w budowie zbiorowości z punktu widzenia określonej cechy statystycznej. W analizie struktury porównuje się również budowę różnych zbiorowości statystycznych z punktu widzenia tej samej cechy statystycznej lub budowę tej samej zbiorowości w różnych okresach.

W analizie struktury wykorzystuje się wskaźniki struktury.

Wskaźnik struktury jest to wyrażony w procentach stosunek wielkości poszczególnych części zbiorowości do wielkości całej zbiorowości

Oznaczając symbolem N liczebność całej zbiorowości, a symbolami
,
,
,
liczebności poszczególnych części tej zbiorowości, wskaźniki struktury można zapisać następująco:

,
,

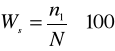
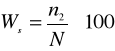
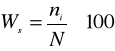
Suma wskaźników struktury równa się 100, czyli

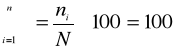
Praktyczne znaczenie wskaźników struktury w analizie struktury polega na przejrzystym przedstawieniu udziału poszczególnych części w całej badanej zbiorowości, oraz na tym ,że pozwalają one na łatwe porównywanie różnych zbiorowości, niezależnie od wielkości bezwzględnych

Wskaźniki struktury nadają się zarówno do analizy szeregów rozdzielczych opartych na cechach mierzalnych , jak i opartych na cechach niemierzalnych.

Szczególnie mają zastosowanie w analizie struktury , kiedy operuje się dużymi liczbami bezwzględnymi.

Wskaźniki struktury pozwalają na łatwe porównywanie wielu zbiorowości, dzięki temu, że wielkość zbiorowości przyjmujemy za 100% , niezależnie od liczb bezwzględnych.

Wskaźniki struktury mogą być wyrażone w ułamkach, w procentach oraz w promille. Najczęściej wykorzystuje się wskaźniki procentowe.

ANALIZA PRZECIĘTNEGO POZIOMU ZJAWISK(TENDENCJI CENTRALNEJ)

Bardziej wnikliwa analiza badanych zbiorowości wymaga ustalenia przeciętnego poziomu wartości cech mierzalnych dla tych zbiorowości.

Przeciętny poziom wartości cech obliczamy za pomocą specjalnych miar statystycznych zwanych ŚREDNIMI (lub przeciętnymi) (są to charakterystyki liczbowe mierzące poziom wartości zmiennej)

Ogólnie miary średnie dzieli się na:

1. ŚREDNIE KLASYCZNE - przy obliczaniu których uwzględniamy wszystkie wartości szeregu statystycznego

1. średnia arytmetyczna

• zwykła

• ważona

2. średnia harmoniczna

2. ŚREDNIE POZYCYJNE - to średnie, które są wartościami konkretnych wyrazów szeregu statystycznego, wyrazów zajmujących w szeregu statystycznym wyraźnie określoną pozycję.

• MEDIANA - wartość środkowa

• DOMINANTA - wartość najczęstsza zw. Modalną lub modą.

ŚREDNIA ARYTMETYCZNA jest to iloraz ogólnej wartości zmiennej i ogólnej liczby jednostek badanej zbiorowości.

Średnią arytmetyczną można obliczyć ze zbioru informacji podanego w formie indywidualnego wyrazu, albo ze zbioru uporządkowanego i poprawionego w formie szeregu rozdzielczego.

1. Jeżeli informacje podano w formie indywidualnego wykazu( szeregu) wartości, które oznaczamy jako

X₁, X₂,...X _n

N = ogólna liczba jednostek zbiorowości

1. 
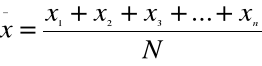
   lub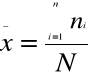
   

NP. obliczamy wzrost przeciętny 10 dziewczynek w grupie VI przedszkola, których wzrost wynosi 130,130,132,132,133,135,135,137,138,138,

130+130+132+132+133+135+135+137+138+138

= ------------------------------------------------------------------------

10

1340

= ----------- = 134 cm

10

Przeciętny wzrost wynosi 134 cm ,a zatem nie odpowiada żadnej konkretnej wartości szeregu żadna bowiem jednostka nie odpowiada wielkości średniej arytmetycznej może być różna od wszystkich poszczególnych wartości szeregu.

Średnia arytmetyczna jest wartością abstrakcyjną.

B. Jeżeli informacje, czyli wartości cech dla których mamy obliczyć średnią arytmetyczną są podane w szeregu rozdzielczym, a nie w szeregu zawierającym wartości wszystkich poszczególnych wyrazów, wówczas obliczamy ŚREDNIĄ ARYTMETYCZNĄ WAŻONĄ.

Wielkości dane Wielkości obliczone

Wzrost dziewczynek w cm Liczba dziewczynek Łączny wzrost dziewczynek

X N X x N

(X₁) - 130 (N₁) 2 X₁ x N₁=130x2=260

(X₂) - 132 (N₂) 2 X₂ x N₂=132x2=264

(X₃) - 133 (N₃) 1 133

(X₄) - 135 (N₄) 2 270

(X₅) - 137 (N₅) 1 137

(X₆) - 138 (N₆) 2 276

=1340/10= 134 cm.

X₁,X₂,X₃ x X_n - indywidualne wartości zmiennej

N₁,N₂,N₃ x N_n - liczebności poszczególnych klas szeregu

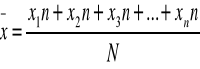
lub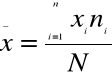

C) Jeżeli mamy do czynienia z szeregiem rozdzielczym, w których wartości zmiennej podano w przedziałach klasowych

• nie mamy dokładnej informacji o każdej jednostce i nie możemy określić dokładnie średniej, możemy jednak uzyskać wartość przybliżoną

• zakładamy, że wartość cechy dla której chcemy obliczyć średnią, wszystkich jednostek należących do danej klasy równa się wartości środka przedziału klasowego

X₁,X₂,X₃,.........X_n - środki przedziałów klasowych

N₁,N₂,N₃,.........N_n - liczebności poszczególnych klas

3)

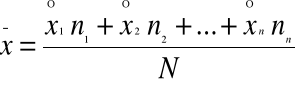
lub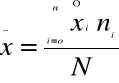

NALEŻY ZAPAMIĘTATĆ ; aby

Średniej arytmetycznej zwykłej nie stosować w przypadkach, w których należy zastosować średnią arytmetyczną ważoną , gdyż prowadzi to do poważnych błędów, np. sprzedano na targowisku 10 kg masła po 32000 zł / kg oraz 20 kg masła po 40000 zł / kg

Obliczyć przeciętną cenę 1 kg masła

32000 zł + 40000 zł

zwykła ------------------------------- = 36000 zł / kg

2

36000 zł x 30 kg = 1080000 według średniej arytmetycznej zmiennej

a rzeczywiście, wartość masła wynosiła

10 kg x 32000 = 320000

20 kg x 40000 = 800000

--------------

1120000

według
ważonej

20 kg x 32000 + 20 kg x 40000

---------------------------------------- = 37,333

30 kg

Np. badając przeciętne płace inżynierów i sprzątaczek nie można ich uznać za zbiorowość jednorodną.

	Liczba zatrudnionych	Wynagrodzenie	Łączne wynagrodzenie
Inżynierowie	10	7000	70.000
Sprzątaczki	2	2500	5.000
RAZEM	12	95.000	75.000

= 75.000 =6.250zł

12

Takie podanie średniej nie ma żadnego logicznego obrazu, albowiem zawyża pace sprzątaczek a zaniża płace inżynierów.

Należy obliczyć odrębnie płace dla tych grup.

POSUMOWANIE:

ŚREDNIA ARYTMETYCZNA jest:

- wielkością mianowaną, tzn. wyrażoną w konkretnych jednostkach miary - X₁ < X < X _n tzn. musi być nie mniejsza od najniższej wartości cechy, ani nie większa od najwyższej wartości cechy

130 134 138

-suma odchyleń od średniej arytmetycznej szeregu =0

MEDIANA

Jest to wartość tego wyrazu w szeregu uporządkowanym, powyżej którego i poniżej którego znajduje się jednakowa liczba obserwacji.

Mediana jest wartością środkowego wyrazu w szeregu uporządkowanym.

Szereg uporządkowany to szereg , w którym wartości cechy mierzalnej są ułożone kolejno od wartości najmniejszej do największej lub odwrotnie.

MEDIANĘ można obliczać:

1. dla szeregów uporządkowanych o nieparzystej liczbie wyrazów- jest ona wówczas konkretną wartością wyrazu środkowego ,tj. wartością wyrazu , którego numer kolejny, tj. miejsce w szeregu jest połową liczby wyrazów szeregu powiększonej o 1.

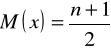
2

np. szereg składający się z 251 wyrazów

M(x)= 251+1 = 126 , czyli medianą jest wartość 126 wyrazu

2

2. dla szeregów o parzystej liczbie wyrazów:

jest ona średnią arytmetyczną wartości dwóch wyrazów środkowych np. w szeregu liczącym 58 wyrazów M(x) jest średnią arytmetyczną 29 i 30 wyrazu(przed wyrazem 29 i po wyrazie 30 jest po 28 wyrazów.)

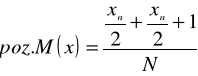
3. dla szeregów rozdzielczych:

należy najpierw

• ustalić numer kolejny obserwacji, której wartość jest medianą

• ustalić klasę , w której znajduje się mediana

• obliczyć dopiero wartość mediany ze wzoru:
  
  
  

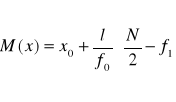
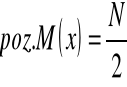
gdzie :

= dolna granica przedziału klasowego w klasie w której znajduje się mediana.

= wielkość przedziału klasowego w klasie w której znajduje się mediana

= liczba obserwacji w klasie w której znajduje się mediana

= ogólna liczba obserwacji, (spostrzeżeń, jednostek statystycznych)

= łączna liczba obserwacji w klasach poprzedzających przedział mediany

Obliczanie mediany jest bardzo wygodne i czasooszczędne. Np. chcąc dowiedzieć się jaka jest mediana wzrostu uczniów II klasy - można ustawić uczniów w szeregu uporządkowanym i zmierzyć wzrost ucznia będącego w środku szeregu ( szeregu nieparzystym) lub dwóch środkowych w przypadku szeregu parzystego i obliczamy medianę jako średnią arytmetyczną ich wartości.

Wartość mediany

• nie zależy od wartości wyrazów skrajnych

• nie zależy od wartości żadnych innych wyrazów leżących poza środkiem uporządkowanego szeregu ( w przypadku średniej arytmetyczne na jej wpływ mają wszystkie wyrazy w szeregu)

Xo
M(x)
X1

Xo = dolna granica przedziału

X1 = górna granica przedziału

KWANTYLE:

Oprócz mediany , stosuje się w statystyce inne miary o podobnym znaczeniu logicznym.

Mediana przepoławia uporządkowany szereg statystyczny. W podobny sposób można obliczyć inne wartości odcinające np. ¼ : ¾ wszystkich spostrzeżeń.

Zbiorowość dzielona na :

4 części to kwartyle

10 części to decyle

100 części to percentyle

1000 części to tercentyle.

Mediana to inaczej kwartyl 2 lub decyl 5.

Kwartyle są to wartości cechy badanej w zbiorowości , które dzielą ją na określone części pod względem liczby jednostek. Części te mogą być równe lub mogą pozostawać do siebie w określonych proporcjach.

Szeregi muszą być uporządkowane .

Do najczęściej używanych kwartyli zaliczamy:

A) kwartyl pierwszy , zwany dolnym - dzieli on

Podstawową czynnością jest kumulacja liczebności (absolutnych , bądź względnych tj. procentowych)

Następnie wyznaczamy pozycję poszczególnych kwartyli w szeregu uporządkowanym , tzn. :

N/4 ; N/2 ; 3N/4

Wykorzystując skumulowane częstości względne (odsetki) otrzymujemy:

POZYCJĘ Q I N/4= 100:4 =25%

POZYCJĘ Q II N/2= 100:2+= 50%

POZYCJĘ Q III 3N /4 = 3*100/4= 75%

Znając pozycję obliczamy wartość poszczególnych kwartyli z poniższych wzorów:

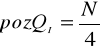
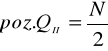
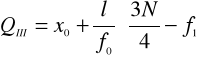
Kwartyle można zaprezentować w układzie współrzędnych, w którym wykreśla się krzywa liczebności skumulowanej ( lun histogram skumulowany)

Jest to łamana, łącząca punkty współrzędnych :górne granice klas i odpowiadające im skumulowane liczby(bezwzględne , bądź względne)

Kwartyle wyznaczamy z szeregu skumulowanego w następujący sposób:

Na osi rzędnych szukamy pozycji kwartyla i prze ten punkt prowadzimy prostą prostopadłą aż do przecięcia się z wielobokiem liczebności. Następnie punkt przecięcia rzutujemy na oś odciętych , na których są oznaczone warianty badanej cechy i odczytujemy wartość danego kwartyla.

Zadanie:

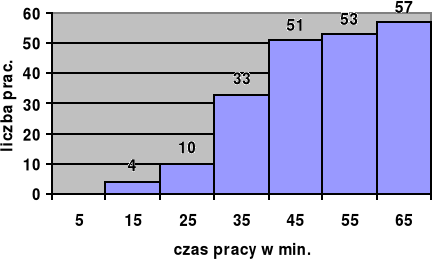
Obliczyć oraz zinterpretować kwartyle na podstawie niżej wymienionych danych:

Pracownicy Przedsiębiorstwa „A „ z Zielonej według czasu dojazdu do pracy w minutach.

Czas dojazdu do pracy w min.	Liczba pracowników	Skumulowana liczba pracow.	Wsk. struktury W %	Skumulowane wsk. strukt.
5-15	4	4	7,0	7,0
15-25	6	6+4= 10	10,5	10,5+7,0=17,5
25-35	23	10+23=33	40,4	40,4+17,5=57,9
35-45	18	18+33=51	31,6	31,6+57,9=89,5
45-55	2	2+51=53	3,5	3,5+89,5=93,0
55-65	4	4+53=57	7,0	7,0+93,0=100,0
Razem	57		100,0

Źródło: dane umowne

N= 57 pracowników

Szukamy pozycji kwartyli:

QI= N/4= 57:4=

QII= M(x) = N/2= 57:2=28,5

QIII= 3N/4= (3*57)/4=

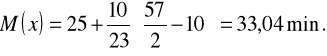
Mediana wynosząca 33,04 min. Oznacza, że środkowy pracownik Przedsiębiorstwa A dojeżdża do pracy w czasie 33,04 min, co oznacza również, że połowa pracowników dojeżdża do pracy w czasie krótszym niż 33,04 min , a druga połowa w czasie dłuższym niż 33,04 minut.

Wykres:

PODSUMOWANIE ŚREDNICH:

ŚREDNIE POZYCYJNE :DOMINANTA i MEDIANA mogą zastępować średnią arytmetyczn --> ą[Author:BBS] ą , najczęściej jednak uzupełniają ją i są stosowane jeśli spełnione są określone warunki. Na ich poziom nie mają wpływu wartości krańcowe. Mogą być stosowane także wtedy, gdy krańcowe wartości oraz odpowiadające im liczebności są nieznane, a znana jest ogólna suma liczebności.

Zasadnicze różnice pomiędzy średnimi klasycznymi , a średnimi pozycyjnymi z punktu widzenia rachunkowego polegają na tym, że przy średnich klasycznych uwzględnia się wszystkie wartości zmiennej (x) i wszystkie liczebności (n), natomiast przy średnich pozycyjnych tylko niektóre zmienne i niektóre liczebności.

Przy obliczaniu średnich klasycznych wartości zmiennej nie muszą być uporządkowane, a przy średnich pozycyjnych warunek ten jest konieczny.

DOMINANTA

Dominanta jest to taka wartość zmiennej x , która w uporządkowanym szeregu rozdzielczym występuje z największą częstotliwością, a tym samym odpowiada jej największa liczebność szeregu (n).

Dominanta nazywana jest często średnią typową, lub wartością najczęstszą, lub wartością modalną.

W szeregach wyliczających i rozdzielczych punktowych dominanta jest tą wartością cechy, której odpowiada największa liczebność( odczytujemy bezpośrednio najliczniejszą wartość z szeregu)

Np. Sklepy w miejscowości X wg liczby sprzedawców - stan w dniu 31.03.1999

Liczba sprzedawców	Liczba sklepów
1	20
2	15
3	24
4 i więcej	7

Źródło: dane umowne

W w/w przykładzie dominują sklepy zatrudniające 3 sprzedawców.

W szeregach rozdzielczych przedziałowych bezpośrednio można określić tylko przedział, w którym znajduje się dominanta - jest to przedział o największej liczebności.

Natomiast konkretną wartość liczbową należącą do tego przedziału i będącą dominantą wyznacza się ze wzoru:

= dolna granica przedziału w którym znajduje się dominanta( klasy najliczniejszej)

= liczebność klasy najliczniejszej

= liczebność klasy poprzedzającej klasę najliczniejszą.

= liczebność klasy następnej po klasie najliczniejszej.

= rozpiętość przedziału klasowego klasy dominującej

Wyznaczanie dominanty na podstawie powyższego wzoru możliwe jest tylko wtedy , gdy:

• rozpiętość przedziałów klasowych jest jednakowa, albo przynajmniej trzy przedziały tj. przedział dominujący oraz dwa sąsiadujące z nim przedziały mają jednakową rozpiętość .

• w szeregu występuje wyraźna tendencja centralna

• występuje jeden ośrodek dominujący ( wyraźne skupienie największej części jednostek wokół jednej wartości)

Wystąpienie większej ilości ośrodków oznacza , że w szeregu jest więcej niż jedna dominanta , a to sugeruje ,że mamy do czynienia ze zbiorowością niejednorodną.

• Szereg nie może być skrajnie asymetryczny, z otwartym przedziałem dominującym(ostatnim lub pierwszym w szeregu)

DOMINANTĘ można wyznaczyć graficznie, wykreślając histogram dla trzech przedziałów- przedziału dominanty i dwóch przydziałów sąsiednich(przyległych),

Tj. przedział poprzedzający i przedział następny po dominancie.

Następnie z górnej podstawy najwyższego prostokąta wykreślamy dwie przekątne łączące najbliżej położone punkty górnych podstaw sąsiednich prostokątów, a następnie z punktu przecięcia się przekątnych wykreślamy prostopadłą do osi odciętych. Prostopadła ta wyznacza na osi odciętych wielkość dominanty.

• Jeżeli liczebność przedziału następnego po przedziale dominanty jest większa niż liczebność przedziału poprzedzającego, to dominanta ma wartość bliższą górnej granicy przedziału w której jest zawarta.

• Jeżeli liczebność przedziału następnego po przedziale dominanty jest mniejsza niż liczebność przedziału poprzedzającego, to dominanta ma wartość bliższą dolnej granicy przedziału dominanty.

• Jeżeli liczebność przedziału klas następnej i poprzedzającej przedział dominanty są równe , wówczas dominanta jest równa środkowi przedziału dominanty.

Reasumując: dominanta charakteryzuje typowy poziom wartości zmiennej badanej cechy występującej z największą częstotliwości.

Dominanta posiada następujące zalety i wady:

• Zaletą jest to, że nie ulega wpływom wartości skrajnych,

• Wadą że w wielu przypadkach jej dokładne obliczanie staje się niemożliwe

( więcej niż jedna dominująca wartość , oraz szeregi z nierównymi przedziała-

mi klasowymi)

Zadanie:

Obliczyć oraz zinterpretować dominantę na podstawie niżej wymienionych danych:

Pracownicy Przedsiębiorstwa „A „ z Zielonej według czasu dojazdu do pracy w minutach.

Czas dojazdu do pracy w min.	Liczba pracowników	Wsk. Struktury W %
5-15	4	7,0
15-25	6	10,5
25-35	23	40,4
35-45	18	31,6
45-55	2	3,5
55-65	4	7,0
Razem	57	100,0

Źródło: dane umowne

N= 57 pracowników

Szukamy przedziału dominanty:

Dominanta znajduje się w przedziale od 25-30 minut.

Następnie z nw wzoru obliczamy dominantę:

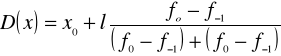
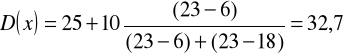
Dominanta wynosi 32,7 minut , co oznacza, że dominują pracownicy dojeżdżający do pracy w czasie 32,7 minut.

Wykres

ZRÓŻNICOWANIE ZBIOROWOŚCI STATYSTYCZNEJ:

MIARY ROZPROSZENIA zwane miarami zróżnicowania lub dyspersji

W skład zbiorowości statystycznej wchodzą jednostki nieidentyczne.

Z punktu widzenia analizy struktury , podstawowe znaczenie ma to, w jakim stopniu jednostki różnią się między sobą pod względem wartości badanej cechy.

Poznane wcześniej miary, jak średnia arytmetyczna , median, czy dominanta nie zawsze w dostateczny sposób charakteryzują zbiorowość statystyczną. Np. średnia arytmetyczna jest wartością abstrakcyjną, abstrahuje od różnic indywidualnych, zaciera je, poprzez wyrażenie tendencji centralnej jedną liczbą.

Obliczona dla różnych zbiorowości może dać wynik identyczny, co wcale nie musi oznaczać, że rozpatrywane struktury są identyczne.

Dlatego bardzo ważnym problemem jest pomiar i liczbowe określenie wielkości zróżnicowania wartości badanej cech, a więc analiza rozproszenia zwana analizą dyspersji, zmienności, odchyleń, zróżnicowania, która polega na badaniu różnic między poszczególnymi wartościami cechy jednostek statystycznych.

Poznane miary przeciętne nie pozwalały wniknąć w wewnętrzną strukturę badanej zbiorowości, a nawet ją zacierają.

Prezentuje to poniższy przykład:

Wynagrodzenie za miesiąc marzec 1998 roku trzech grup pracowników , z których każda składa się z trzech osób, przedstawia się następująco:

GRUPA 1 GRUPA 2 GRUPA 3

1.634 1.485 880

M(x)1.782 M(x) 1.782 M(x) 1.872

1.930 2.079 2.684

Σ= 5.346 Σ= 5.346 Σ= 5.346

= 5.346:3=1.782
= 5.346:3=1.782
= 5.346:3=1.782

Średnie arytmetyczne oraz mediany płac dla wszystkich trzech grup są jednakowe i wynoszą 1.782 zł., ale grupy te nie są jednakowe pod względem zróżnicowania, tj. rozproszenia płac.

W I grupie płace są mało zróżnicowane, ale w III grupie rozpiętość płac jest bardzo duża- trzykrotnie zarabiającego wyższe wynagrodzenie od najniżej zarabiającego.

Dlatego też stosuje się miary rozproszenia , polegające na ustaleniu , w jakim stopniu poszczególne jednostki różnią się od siebie.

Do najczęściej stosowanych miar rozproszenia należą:

• Obszar zmienności zwany rozstępem R

• Odchylenie przeciętne d(x)

• Odchylenie standardowe S(x)

• Współczynnik zmienności V(x)

Obszar zmienności zwany rozstępem R - jest najprostszą miarą rozproszenia i określa różnicę między wartością największą a najmniejszą w badanej zbiorowości

Obliczamy go ze wzoru:

R= X max - X min

Jest to miara bardzo prosta do obliczania, jednocześnie bardzo prymitywna, gdyż jej wielkość zależy od wielkości skrajnych, które mogą być przypadkowe. Miara ta posiada małą wartość poznawczą, ponieważ do jej obliczenia wykorzystuje się tylko najniższą i najwyższą wartość cechy.

Wielkość rozstępu będzie wysoka nie tylko wtedy , gdy zmienność jest rzeczywiście duża , ale również wtedy , gdy wartość jednej jednostki przypadkowo odbiega od pozostałych, mało zróżnicowanych.

Poprawna miara zmienności musi zatem uwzględniać cały rozkład liczebności w szeregu.

ODCHYLENIE PRZECIĘTNE- jest miarą bardziej precyzyjną niż obszar zmienności.

Uwzględnia nie tylko wartości skrajne , ale wszystkie wartości pośrednie.

Charakteryzuje ono przeciętny poziom odchyleń faktycznych wartości szeregu od średniej arytmetycznej.

Inaczej: jest to średnia arytmetyczna bezwzględnych wartości odchyleń poszczególnych jednostek zbiorowości Xi od ich średniej arytmetycznej.

Odchylenie przeciętne może być obliczane dla indywidualnego wykazu wartości lub dla szeregu rozdzielczego .

Ogólnie określamy go wzorem

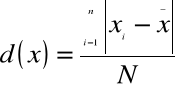
gdzie:

= to poszczególne wartości zmiennej

= średnia arytmetyczna

N = liczba obserwacji (suma jednostek statystycznych, obserwacji, spostrzeżeń )

Rozróżniamy:

1. odchylenie przeciętne proste

2. odchylenie przeciętne ważone

Odchylenie przeciętne proste obliczamy wówczas , gdy wartości zmiennej podane są w szeregu indywidualnym. Obliczamy go ze wzoru:

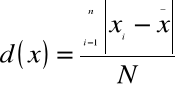
gdzie:

= wartości cechy

= średnia arytmetyczna

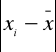
= wartość bezwzględna różnic pomiędzy poszczególnymi wartościami cechy a średnią arytmetyczną.

N = suma jednostek statystycznych( obserwacji, spostrzeżeń, )

Zadanie 1.

Obliczyć przeciętne zróżnicowanie mając nw. Dane dotyczące wynagrodzenia w rodzinie Balskich z Iławy we wrześniu 1998 roku

Wyszczególnienie	Wynagrodzenie w zł.	x-
Matka	1.200	1.200-1.340=-140	140
Ojciec	3.000	1.660	1.660
Starszy syn	800	-540	540
Młodszy syn	1000	-340	340
Córka	700	-640	640
Razem	6.700		3.320

Źródło: dane umowne

= 6.700:5=1.340ZŁ

d(x)= 3.320 : 5 = 664 zł.

Interpretacja : Faktyczne wynagrodzenia w rodzinie Balskich różnią się średnio o 664 zł od przeciętnej płacy wynoszącej w ich rodzinie 1.340 zł.

Odchylenie przeciętne ważone

Odchylenie przeciętne ważone stosujemy wówczas, gdy wartości zmiennej są podane nie w szeregu indywidualnym, lecz w szeregu rozdzielczym- punktowym lub w opartych na przedziałach klasowych.

Odchylenie przeciętne ważone dla szeregu rozdzielczego - punktowego obliczamy ze wzoru:

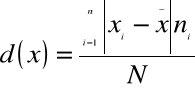
ZADANIE 2.

Obliczyć przeciętne zróżnicowanie gospodarstw domowych pod względem liczby osób w rodzinie w Iławie w dniu 30.09 2000 roku:

Gospodarstwa domowe według liczby osób w rodzinie.

Liczba osób w rodzinie	Liczba gospodarstw	Łączna liczba osób w gospodarstwach	Odchylenia od średniej	Bezwzględne odchylenia od średniej	Iloczyn bezwzg. Odchylń i liczebności
2	12	2*12=24	2-3,7=-1,7	1,7	1,7*12=20,4
3	18	54	3-3,7= - 0,7	0,7	0,7*18=12,6
4	35	140	0,3	0,3	10,5
5	15	75	1,3	1,3	19,5
	∑= 80	∑=293			∑=63

Źródło: dane umowne

=293:80=3,7 osób

d(x) =63:80= 0,8 osób

Odp. Liczba osób w badanych gospodarstwach domowych różniła się przeciętnie o 0,8 osób od średniej liczby osób w rodzinie wynoszącej 3,7 osób.

Odchylenie przeciętne ważone dla szeregu rozdzielczego zbudowanego w oparciu o przedziały klasowe:

gdzie:

= liczebność i-tego przedziału

= środek przedziału ( jako średnia arytmetyczna dolnej i górnej granicy przedziału)

ZADANIE 3

Obliczyć przeciętne zróżnicowanie płac wybranej grupy osób w Iławie w dniu 20.09 2000 roku:

Płaca w zł.	Liczba osób
1.400-1.800	5	1.600	5*1.600= 8.000	1.600-2.360 = -760	760	760*5= 3.800
1.800-2.200	20	2.000	20*2.000= 4.000	2.000-2.360 = -360	360	360*20= 7.200
2.200-2.600	60	2.400	144.000	40	40	2.400
2.600-3.000	10	2.800	28.000	440	440	4.400
3.000-3.400	5	3.200	16.000	840	840	4.200
Razem	100		236.000			22.000

Źródło: dane umowne

= 236.000:100= 2.360zł.

d(x)=22.000:100=220zł.

W badanej grupie 100 osób płace we wrześniu 2000roku przeciętnie różniły się

O 220zł od ich średniej pacy wynoszącej 2.360zł.

ODCHYLENIE STANDARDOWE:

Odchylenie standardowe różni się od bezwzględnych wartości odchyleń przeciętnych, ale wykazują takie same tendencje.

Możemy go obliczać dla:

a) indywidualnego wykazu wartości:

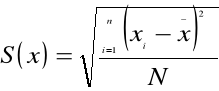
←odchylenie standardowe proste

b) dla szeregu rozdzielczego punktowego:

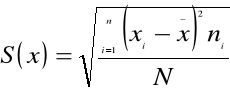
←odchylenie standardowe ważone

3. dla szeregu rozdzielczego opartego na przedziałach klasowych

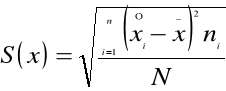
←odchylenie standardowe ważone

WSPÓŁCZYNNIK ZMIENNOŚCI

Zarówno miary rozproszenia, jak i wartości średnie są liczbami mianowanymi.

Każdy parametr dotyczący rozproszenia wyrażony jest w tych samych jednostkach miary(metry, tony , godziny , lata ,itp.) w jakich podana jest wartość cechy zmiennej szeregu.

Fakt ten uniemożliwia bezpośrednie porównywanie tych miar obliczonych dla różnych szeregów.

Nie zawsze też można porównywać miary rozproszenia obliczone dla szeregów o tej samej skali pomiarowej. Np. przy obliczaniu dyspersji płac inżynierów i sprzątaczek nie uzasadnione byłoby bezpośrednie porównywanie odchyleń standardowych, ponieważ średni poziom płac w tych dwóch grupach zatrudnionych różni się istotnie. Gdy średnie obliczone dla dwóch szeregów mających ten sam charakter , istotnie się różnią, należy oczekiwać, że również zmienność mierzona w liczbach absolutnych kształtować się będzie na różnym poziomie.

Dlatego gdy badane zjawisko mierzone jest w różnych jednostkach miary lub kształtuje się na niejednakowym poziomie przeciętnym , do oceny (do porównań) rozproszenia należy stosować współczynnik zmienności

Informuje on nas o sile dyspersji . Duża jego wartość liczbowa świadczy o niejednokrotności zbiorowości.

Współczynnik zmienności znajduje zastosowanie szczególnie w tych przypadkach kiedy istnieje konieczność porównania rozproszenia dwóch zbiorowości ( dwóch różnych zjawisk), np. płace oraz wiek pracowników.

Dysponując informacjami dotyczącymi :

S(x) dla płac = 150zł.

S(x) dla wieku = 5 lat

Trudno powiedzieć ze względu na którą cechę pracownicy są bardziej zróżnicowani, albowiem informacje podane są w różnych jednostkach miary.

WSPÓŁCZYNNIK ZMIENNOŚCI pozwala na ustalenie wyrażonego w procentach zróżnicowania faktycznych wartości cechy w zbiorowości statystycznej.

WSPÓŁCZYNNIK ZMIENNOŚCI

jest względną miarą rozproszenia . Obliczmy go dzieląc odchylenie przeciętne lub standardowe przez średnią arytmetyczną.

Można go obliczać jako:

a) wyrażoną w % relację odchylenia przeciętnego do średniej arytmetycznej

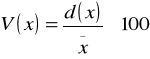
b) lub wyrażoną w % relację odchylenia standardowego do średniej arytmetycznej

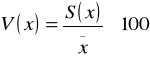
ANALIZA DYNAMIKI ZJAWISK

Omówione dotychczas miary statystyczne służą do badania poszczególnych cech badanego zjawiska (struktury, natężenia , poziomu przeciętnego, stopnia zróżnicowania) w ujęciu statycznym tj. w danym momencie albo w danym okresie, nie charakteryzują natomiast dynamiki zjawisk , tj. zmian zachodzących w czasie .

Tymczasem wszystkie zjawiska gospodarcze znajdują się w ciągłym ruchu, rozwoju, zachodzą w nich nieustanne zmiany.

Istnieje więc potrzeba analizowania rozwoju badanego zjawiska w czasie.

Analiza dynamiki polega na ustalaniu stopnia wzrostu lub spadku wielkości badanego zjawiska badanego zjawiska za pomocą specjalnych miar dynamiki.

Miary dynamiki służą do badania zmian , jakie następują w zjawiskach czy procesach, na skutek upływu czasu.

Pojęcia wstępne:

Xo = okres podstawowy = to okres, moment przyjmowany za podstawę badań.

Okres podstawowy oznacza punkt odniesienia dla wielkości badanej

Xn = okres badany, który porównujemy z okresem podstawowym.

MIARY DYNAMIKI

1. Przyrost absolutny - jest to różnica między wielkościami badanego zjawiska w okresie badanym a wielkością zjawiska z okresu podstawowego.

Przyrosty mogą być :

a) podstawowe -wybieramy jeden okres za podstawowy w stosunku do którego porównujemy wszystkie wielkości

b) łańcuchowe - za podstawę porównań przyjmuje się okres poprzedzający okres badany.

Przyrost absolutny może być: +, --, lub O

2. Przyrost względny: - odpowiada na pytanie , jakie jest względne tempo zmian w czasie.

Jest to stosunek przyrostu absolutnego do poziomu zjawiska w okresie podstawowym , lub w okresie poprzedzającym okres badany.

Przyrost względny może być:

• Podstawowy

;
;
;

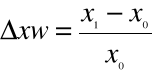
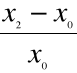
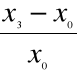
• Łańcuchowy

;
;
;

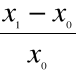
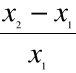
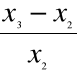
3. Tempo przyrostu - czyi przyrost względny wyrażony w procentach.

Określa wyrażoną w procentach wielkość przyrostu albo zmniejszenia się wielkości badanego zjawiska w okresie badanym w stosunku do wielkości zjawiska z okresu podstawowego lub poprzedzającego okres badany

• Tempo przyrostu o podstawie stałej

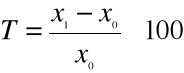
; T=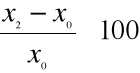
; T=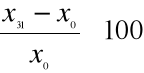

• Tempo przyrostu o podstawie łańcuchowej

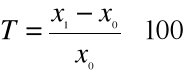
; T=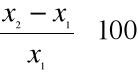
; T=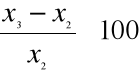

4. INDEKSY - są najczęściej stosowaną w praktyce miara dynamiki.

Indeksem nazywamy stosunek wyrażony zwykle w % wielkości danego zjawiska w okresie badanym do wielkości tego zjawiska w okresie podstawowym lub poprzedzającym okres badany

• Indeksy o podstawie stałej:

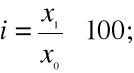
i=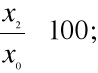
i=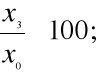

• Indeksy o podstawie łańcuchowej

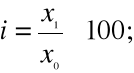
i=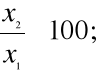
i=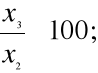

Wartość indeksu mniejsza od 100 informuje nas , że wielkość badanego zjawiska była mniejsza od wielkości zjawiska z okresu przyjętego za podstawę porównań.

Wartość indeksu większa od 100 informuje nas , że wielkość badanego zjawiska była większa od wielkości zjawiska z okresu przyjętego za podstawę porównań

---