0238

239

§ 1. Badanie przebiegu funkcji

Niech    (0<x<Jjc). Pochodna tej funkcji

jest ujemna, gdyż x < tg x. Znaczy to, że funkcja/(x) maleje, a zatem/(x)>f (in) = 2/«, jeśli 0<x<iit.

2) Funkcja/(x) = cos x—l—Jx² jest równa 0 w punkcie x=0. Jej pochodna spełnia dla x>0 nierówność

/'(x)= — sinx+x >0 (bo sinx<x).

Okazuje się więc, że funkcja/(x) jest dla x>0 rosnąca i dla x>0 jest /(x)>/(0), tzn.

cosx> 1 — \x² .

Stąd analogicznie otrzymamy dla x>0 nierówność

sinx>x—$x ³

itd.

3)    Udowodnić, że dla 0 < x < $ tt jest

tgx>x+łx³ .

Wystarczy w tym celu udowodnić, że dla takich wartości x pochodna funkcji tgx —x — Jx³, równa 1/cos² x — 1 —x² jest dodatnia, tzn. że tg² x—x²>0, a to sprowadza się do znanej nierówności tg x>x [54, (9)].

4)    Funkcja/(x) = ln x—x (x>0) ma pochodną

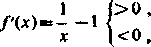
gdy 0<x<l , gdy x> 1,

a zatem funkcja ta rośnie, gdy x zmienia się w przedziale (0,1> i maleje w przedziale <1, -t-oo). Stąd widać, że/(l)= — 1 jest największą wartością funkcji, a zatem dla x>0 zachodzi nierówność

lnx<x—1.

5) Rozpatrzmy jeszcze funkcję /(x)=x“—ax dla x>0 (zakładamy, że 0<ot<l). Ponieważ jej pochodna

gdy 0<x<l , gdy x> I ,

wnosimy analogicznie do 4), że dla x>0 jest

(3)

x^a—ax< 1 —a .

Otrzymana nierówność jest punktem wyjścia do wyprowadzenia wielu nierówności klasycznych. W związku z tym warto przedstawić ją jeszcze w innych postaciach.

Podstawiając x=a/b. gdzie a i A są dowolnymi liczbami dodatnimi, i oznaczając l— a przez /?, sprowadzimy (3) do postaci

(3a)

a‘b^f<aa+bb (a, b, a, 0>O, a + 0=l).

Czasami wprowadza się liczby k= l/a>l i k'=llp >l, a zatem k' = kl(k — 1). Zastępując w poprzedniej nierówności a i b przez a* i b^k otrzymujemy

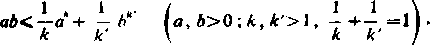
(3b)