0092

94

IX. Całka oznaczona

303. Własności całek wyrażające się równościami. Podamy dalsze własności całek, dające się wyrazić za pomocą równości (¹).

2° Zakładamy, że funkcja f(x) jest całkowalna w największym z przedziałów (a, by, <a, c> i <c, bj (²). Wtedy jest ona całkowalna w dwóch pozostałych przedziałach i ponadto przy dowolnym wzajemnym położeniu a,bic zachodzi równość

f /(*)^dx = f /(*)+ //(*) dx .

a    a    e

Dowód. Przypuśćmy najpierw, że a < c < ó i że funkcja/(jc) jest całkowalna w przedziale <a, ó>.

Całkowalność tej funkcji w przedziałach <a, by i <c, by wynika z własności III [299],

Rozpatrzymy jakikolwiek podział przedziału <a, by na podprzedziały, przy tym punkt c niech będzie jednym z punktów dzielących. Tworząc sumy całkowe, otrzymujemy (sens oznaczeń jest jasny)

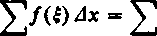
^C/(f)dx+^/(£)dx. a    a    c

Szukaną równość otrzymamy przez przejście do granicy, gdy A -» 0.

Inne przypadki wzajemnego położenia punktów a, b, c sprowadzają się do powyższego. Niech będzie na przykład b < a < c, a funkcja / (x) niech będzie całkowalna w przedziale <c, by lub — co wychodzi na to samo — w przedziale <ó, c>. W tym przypadku, jak udowodniliśmy, jest

jf(x)dx = jf(x)dx+ jf(x)dx,

b    ba

a stąd, po przeniesieniu całek pierwszej i drugiej z jednej strony równości na drugą i po przestawieniu granic (na podstawie własności 1°), otrzymamy znowu poprzednią zależność.

3° Jeśli funkcja f (x) jest całkowalna w przedziale (a, by, to również funkcja kf (x) {gdzie k = const) jest całkowalna w tym przedziale i

J kf{x) dx = k j f(x) dx .

a    a

4° Jeśli funkcje f (x) i g (x) są całkowalne w przedziale <a, by, to również funkcje f(.x)±g (jc) są całkowalne w tym przedziale i

f [f(x)±g W] dx = J f(x) dx± f g (x) dx .

a    aa

W obu przypadkach dowód przeprowadza się analogicznie, rozpatrując sumy całkowe i przechodząc do granicy. Przeprowadzimy go na przykład dla ostatniego twierdzenia.

b

(¹)    Jeśli chodzi o całkę f, to w dalszym ciągu będziemy przyjmowali (już bez specjalnego zaznaczę-

a

nia) za możliwe oba przypadki: a<b\a>b.

(²)    Zamiast tego można założyć, że funkcja jest całkowalna w każdym z dwóch mniejszych przedziałów, a stąd wynika już jej całkowalność w większym przedziale.