Zadanie 1.
Rozpatrujemy eksperyment polegający na wyciagnięciu pojedynczej karty z dobrze potasowanej talii 52 kart. Niech A oznaczać będzie zdarzenie polegające na wyciągnięciu damy, a B zdarzenie polegające na wyciągnięciu pika. Wyznacz prawdopodobieństwa zdarzeń:
a) A, b) B, c) ![]()
d) ![]()
e) ![]()
Zadanie 2.
W urnie znajduje się 5 kul: 3 czerwone i 2 zielone. Zdarzenie A polega na wyciągnięciu za pierwszym razem kuli czerwonej, a zdarzenie B polega na wyciągnięciu za pierwszym razem kuli zielonej. Czym różnią się te zdarzenia od zdarzeń z zadania 1? Wyznacz prawdopodobieństwa zdarzeń:
a) A, b) B, c) ![]()
d) ![]()
Zadanie 3.
Dziecko bawiąc się literami A, A, K, S, S, T, T, T, Y, Y, układa różne słowa. Jakie jest prawdopodobieństwo tego, że przypadkowo złoży słowo STATYSTYKA?
Zadanie 4.
Rozpatrujemy eksperyment polegający na wyciagnięciu dwóch kart (bez zwracania) z dobrze potasowanej talii 52 kart. Niech A oznaczać będzie zdarzenie polegające na wyciągnięciu za drugim razem damy, a B zdarzenie polegające na wyciągnięciu za pierwszym razem pika. Wyznacz ![]()
.
Zadanie 5.
Z urny zawierającej 4 kule z numerami 1, 2, 3, 4 losujemy dwie kule bez zwracania. Jakie jest prawdopodobieństwo wylosowania za drugim razem kuli o numerze parzystym pod warunkiem, że za pierwszym razem wylosowaliśmy kulę o numerze nieparzystym?
Zadanie 6.
Obliczyć, czy jednakowe jest prawdopodobieństwo wygrania w loterii zawierającej n biletów, spośród których jeden wygrywa, i w loterii zawierającej 2n biletów, spośród których dwa wygrywają, jeśli:
gracz kupuje jeden bilet,
gracz kupuje dwa bilety.
Zadanie 7.
Prawdopodobieństwo, że cena ropy naftowej pójdzie jutro w górę wynosi 0,3, a prawdopodobieństwo, że cena złota pójdzie w górę wynosi 0,2. Wiadomo ponadto, że w 6% przypadków obie ceny idą w górę. Czy ceny obu towarów są od siebie niezależne?
Zadanie 8.
W urnie znajdują się 4 kule: biała, czerwona, czarna oraz trójkolorowa zawierająca trzy poprzednie kolory. Niech A, B, C oznaczają wylosowanie kuli zawierającej kolor odpowiednio biały, czerwony i czarny. Czy zdarzenia A, B, C są:
a) niezależne parami, b) wzajemnie niezależne?
Zadanie 9.
Prawdopodobieństwo, że do konsumenta dotrze reklama telewizyjna pewnego produktu wynosi 0,04, natomiast prawdopodobieństwo, że zauważy on plakat reklamowy na ulicy wynosi 0,06. Oba te zdarzenia uważamy za niezależne.
Jakie jest prawdopodobieństwo, że do konsumenta dotrą obie formy reklamy?
Jakie jest prawdopodobieństwo, że do konsumenta dotrze przynajmniej jedna forma reklamy?
Zadanie 10.
Z urny zawierającej losy o numerach 1-16 losujemy jeden los. Oznaczmy zdarzenia:
A - wylosowanie liczby większej niż 8,
B - wylosowanie liczby podzielnej przez 4,
C - wylosowanie jednej z liczb: 1, 2, 3, 4, 5, 6, 7, 9.
Czy zdarzenia A, B, C są:
a) niezależne parami, b) wzajemnie niezależne?
Zadanie 11.
W fabryce produkującej samochody istnieją trzy taśmy montażowe, które produkują odpowiednio 25%, 35%, 40% całej produkcji. Wiadomo, że z każdej taśmy schodzi odpowiednio 5%, 4% i 2% samochodów z pewną usterką. Wybieramy losowo jeden samochód. Oblicz prawdopodobieństwo, że:
został on wyprodukowany na pierwszej taśmie,
posiada usterkę,
nie posiada usterki,
został wyprodukowany na pierwszej taśmie, jeśli stwierdzono, że posiada usterkę.
Zadanie 12.
W urnie znajduje się 5 kul: 3 czarne i 2 białe. Losujemy kulę i zwracamy dosypując jeszcze 3 tego samego koloru co wylosowana. Losujemy drugi raz kule z urny. Jakie jest prawdopodobieństwo, że za drugim razem wylosujemy kulę czarną?
Zadanie 13.
Stefan - student statystyki, zastanawia się czy zasiąść dzisiejszego wieczoru do nauki, czy iść na imprezę. Postanowił powierzyć sprawę losowi. Przygotował dwie urny z białymi i czarnymi kulami, przy czym w pierwszej umieścił 2 kule białe i 8 czarnych, a w drugiej 6 kul białych i 4 czarne. Najpierw rzucał kostką do gry, jeżeli wypadła liczba parzysta losował kule z pierwszej urny, jeżeli wypadła liczba nieparzysta losował kulę z drugiej urny. Wylosowanie kuli białej oznaczało naukę, czarnej zaś zabawę.
Jakie jest prawdopodobieństwo wylosowania kuli białej?
Stefan poszedł na imprezę, jakie jest prawdopodobieństwo, że losował kulę z drugiej urny?
Zadanie 14.
Na 100 kierowców-mężczyzn przypada 5, którzy w ciągu minionego roku spowodowali wypadek, na 1000 kierowców-kobiet przypadają 2, które w ciągu minionego roku spowodowały wypadek. Z bazy kierowców (o jednakowej liczbie mężczyzn i kobiet) wybrano losowo jedną osobę i okazało się że spowodowała ona wypadek w ciągu ostatniego roku. Jakie jest prawdopodobieństwo, że jest to mężczyzna?
Zadanie 15.
W przedsiębiorstwie X pracują 64 osoby. Podział pracowników ze względu na zarobki oraz płeć przedstawia poniższa tablica:
Zarobki Płeć |
|
|
|
Kobieta |
10 |
22 |
32 |
Mężczyzna |
2 |
30 |
32 |
|
12 |
52 |
64 |
Wybieramy losowo jednego pracownika. Oznaczmy zdarzenia: A - wybrano kobietę, B - wybrano osobę zarabiającą poniżej 3000 zł. Obliczyć:
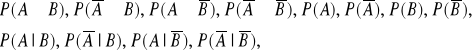
Czy zdarzenia A i B są niezależne?
Zadanie 16.
Obliczyć prawdopodobieństwo, że wybrany w sposób losowy punkt kwadratu: |x|<1, |y|<1, jest punktem leżącym wewnątrz okręgu o równaniu ![]()
.
Zadanie 17.
Obliczyć prawdopodobieństwo, że wybrany w sposób losowy punkt kwadratu: |x|<4, |y|<4, jest punktem leżącym na zewnątrz okręgu o równaniu ![]()
.
Zadanie 18.
Losujemy dwie liczby p i q z przedziału <0,1> i budujemy trójmian kwadratowy ![]()
. Jakie jest prawdopodobieństwo, że ten trójmian będzie miał dwa pierwiastki?
Zadanie 19.
Losujemy dwie liczby p i q z przedziału <-1,1> i budujemy trójmian kwadratowy ![]()
. Jakie jest prawdopodobieństwo, że ten trójmian będzie miał dwa pierwiastki?
Zadanie 20.
Na płaszczyźnie poprowadzono proste równoległe odległe o 2a. Na płaszczyznę tę rzucamy w sposób przypadkowy monetę o promieniu r < a. Znaleźć prawdopodobieństwo tego, że moneta nie przetnie żadnej prostej.
Zadanie 21.
Niech:
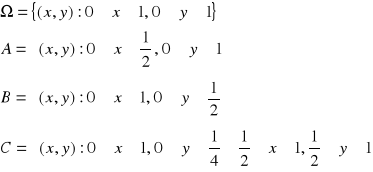
Czy zdarzenia A, B, C, są niezależne?
Zadanie 22.
W sposób losowy kreślimy cięciwy okręgu. Obliczyć prawdopodobieństwo, że cięciwa jest krótsza od boku trójkąta równobocznego wpisanego w okrąg.
Zadanie 23.
Stefan - student statystyki, nie ma poczucia czasu i zawsze spóźnia się na wykład trwający 90 minut. Przybycie na wykład w dowolnym przedziale czasowym podczas trwania wykładu jest dla niego tak samo prawdopodobne jak w każdym innym przedziale o tej samej długości. Jakie jest prawdopodobieństwo, że Stefan:
nie spóźni się na wykład,
spóźni się nie więcej niż 15 minut,
przyjdzie w ciągu godziny od rozpoczęcia wykładu,
przyjdzie w ciągu ostatnich 15 minut wykładu.
Zadanie 24.
Wyszukiwarka internetowa Google podaje wyniki wyszukiwania w czasie od 0,01 do 0,9 sekundy. Znalezienie się czasu trwania operacji w którymkolwiek podprzedziale tego przedziału jest tak samo możliwe, jak znalezienie się w innym podprzedziale o tej samej długości. Jakie jest prawdopodobieństwo, że operacja wyszukiwania będzie trwała:
1/1000 sekundy,
0,2 sekundy,
mniej niż 0,3 sekundy,
pomiędzy 0,3 a 0,6 sekundy,
pomiędzy 0,8 a 1 sekundą,
więcej niż 0,99 sekundy.
Rachunek prawdopodobieństwa 17-02-09
1
Wyszukiwarka
Podobne podstrony:
3 zadania z rachunku prawdopodobieństwa, RACHUNEK PRAWDOPODOBIEŃSTWA CZ
Rachunek prawdopodobienstwa cz.2
Rachunek prawdopodobieństwa, cz 2
Rachunek prawdopodobieństwa, cz 1
Kombinatoryka Rachunek Prawdopodobieństwa Zadania cz 6
Kombinatoryka Rachunek Prawdopodobieństwa Zadania cz 4
Krysicki Rachunek prawdopodobieĹ stwa i statystyka matematyczna cz 1
Kombinatoryka Rachunek Prawdopodobieństwa Zadania cz 5
Kombinatoryka Rachunek Prawdopodobieństwa Teoria cz 4
Kombinatoryka Rachunek Prawdopodobieństwa Zadania cz 4
Kombinatoryka Rachunek Prawdopodobieństwa Teoria cz 2
Kombinatoryka Rachunek Prawdopodobieństwa Teoria cz 6
Krysicki i inni Rachunek prawdopodobienstwa i statystyka matematyczna w zadaniach cz I
Kombinatoryka Rachunek Prawdopodobieństwa Teoria cz 3
Rachunek prawdopodobienstwa i statystyka matematyczna w zadaniach cz 2
Kombinatoryka Rachunek Prawdopodobieństwa Zadania cz 5
Kombinatoryka Rachunek Prawdopodobieństwa Teoria cz 5
Kombinatoryka Rachunek Prawdopodobieństwa Teoria cz 4
Kombinatoryka Rachunek Prawdopodobieństwa Teoria cz 1
więcej podobnych podstron