Politechnika Gdańska Wydział Budownictwa Lądowego
Katedra Fizyki Technicznej Rok akademicki 1997 / 98
i Matematyki Stosowanej
Laboratorium z FIZYKI
Temat: Badanie elipsoidy bezwładności bryły sztywnej za pomocą wahadła skrętnego
Grupa 2 Rzodkiewicz Michał
Wstęp
Doświadczenie polega na zbadaniu elipsoidy bezwładności i sporządzeniu jej wykresu. Posługujemy się przy tym wahadłem skrętnym, zwanym także torsyjnym dla którego zastosowanie mają poniższe wzory.
Równanie ruchu układy ma postać:
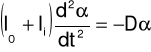
gdzie: I0 - moment bezwładności pustej ramki,
Ii - moment bezwładności bryły względem badanej osi,
α - kąt obrotu ramki,
D - moduł sztywności drutu.
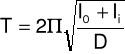
Okres drgań skrętnych układu jest równy:
W celu dokonania pomiarów należy znaleźć amplitudę roboczą, tzn. taką dla której wartość okresu nie zależy od wychylenia.
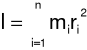
Moment bezwładności układu mechanicznego względem nieruchomej osi jest wielkością fizyczną równą sumie iloczynów mas wszystkich n punktów materialnych układu i kwadratów ich odległości od osi:
gdzie: mi - masa i-tego punktu materialnego,
ri - odległość i-tego punktu materialnego od konkretnej osi.
![]()
Moment bezwładności bryły ciągłej obliczamy zastępując sumowanie całkowaniem:
gdzie: ρ - masa właściwa ciała,
r - odległość elementu objętości od konkretnej osi.
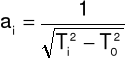
Elipsoidę bezwładności rysujemy rysując jej przekroje w płaszczyznach Oxy,Oxz,Oyz. Wzdłuż każdego kierunku odkładamy odcinek:
gdzie: Ti - okres drgań ramki z badanym ciałem wokół konkretnej osi obrotu,
T0 - okres drgań pustej ramki.
Obliczenia
Amplituda robocza
T1 = 18,620 s α1 = 60°
T2 = 18,608 s α2 = 30°
T1 ≈ T2 αr = const = 30°
2. Długości odcinków na poszczególne osie (bryła 1).
T0 = 1/30(T01 + T02 + T03) = 0,94587 s
Tx = 1/30(Tx1 + Tx2 + Tx3) = 1,86087 s
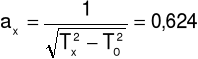
Ty = 1/30(Ty1 + Ty2 + Ty3) = 1,86123 s
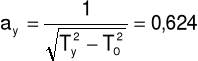
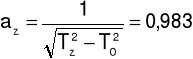
Tz = 1/30(Tz1 + Tz2 + Tz3) = 1,389 s
Td = 1/30(Td1 + Td2 + Td3) = 1,56 s
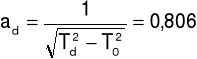
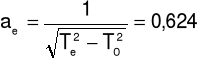
Te = 1/30(Te1 + Te2 + Te3) = 1,862 s
Tf = 1/30(Tf1 + Tf2 + Tf3) = 1,497 s
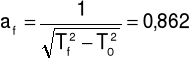
3. Długości odcinków na poszczególne osie (bryła 2).
Po analogicznych obliczeniach mamy:
ax = 0,623
ay = 0,666
az = 0,992
ad = 0,817
ae = 0,649
af = 0,896
Rachunek błędu
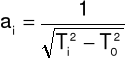
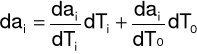
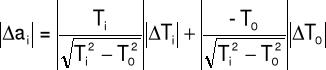
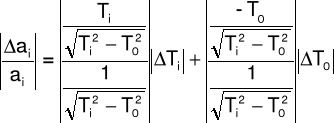
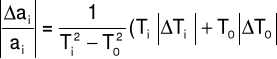
Obliczenia błędów
1. Bryła 1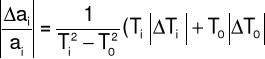
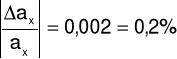
Δax = 0,001
ax = axo ± Δax = 0,624 ± 0,001
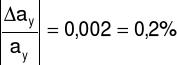
Δay = 0,001
ay = ayo ± Δay = 0,624 ± 0,001
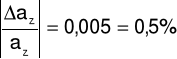
Δaz = 0,004
az = azo ± Δaz = 0,983 ± 0,004
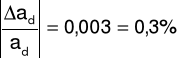
Δad = 0,003
ad = ado ± Δad = 0,806 ± 0,003
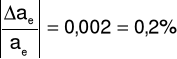
Δae = 0,001
ae = aeo ± Δae = 0,624 ± 0,001
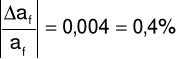
Δaf = 0,001
af = afo ± Δaf = 0,624 ± 0,001
2. Bryła 2 - analogicznie
ax = axo ± Δax = 0,624 ± 0,001
ay = ayo ± Δay = 0,624 ± 0,002
az = azo ± Δaz = 0,983 ± 0,005
ad = ado ± Δad = 0,806 ± 0,003
ae = aeo ± Δae = 0,624 ± 0,002
af = afo ± Δaf = 0,624 ± 0,003
Wnioski
Zastosowanie fotokomórki pozwoliło na znaczne zwiększenie dokładności pomiaru okresu, co na pewno ma wpływ na przebieg elipsoidy. Gdybyśmy znali wartość modułu sztywności pręta na którym wisiała ramka moglibyśmy wyliczyć wartości momentów bezwładności na poszczególne osie.
1
2
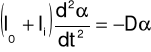
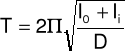
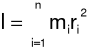
![]()
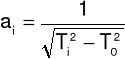
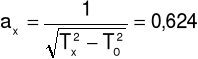
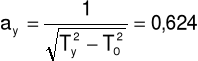
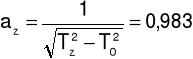
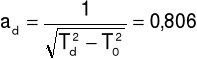
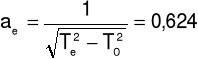
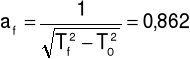
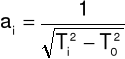
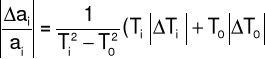
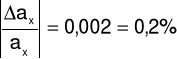
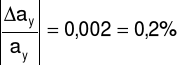
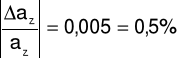
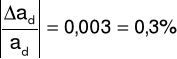
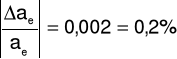
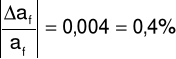
Wyszukiwarka
Podobne podstrony:
Fizyka labolatorium, Laboratorium z Fizyki (4), Labrotorium z Fizyki
Fizyka labolatorium, Laboratorium z Fizyki (4), Labrotorium z Fizyki
Fizyka labolatorium, Laboratorium z Fizyki (6), Laboratorium z Fizyki
Laboratorium z Fizyki, Politechnika Gdańska
Fizyka labolatorium, Laboratorium z Fizyki (5), Laboratorium z Fizyki
Fizyka26-SW, Laboratorium fizyki ogólnej
Laboratorium fizyki CMF PŁ, Elektronika i Telekomunikacja, z PENDRIVE, Politechnika - EiT, 2011 - s
Wzór sprawozdania na labolatoria z fizyki, Politechnika, Labolatoria Fizyka
EM 3.2, Politechnika Lubelska, Studia, semestr 5, Sem V, Sprawozdania, sprawozdania, Sprawozdania, L
J 4.1(2), Politechnika Lubelska, Studia, semestr 5, Sem V, Sprawozdania, sprawozdania, Sprawozdania,
FIZA W68 MOJE, 1 STUDIA - Informatyka Politechnika Koszalińska, finish, Fizyka, fiza, spr, fizyka,
J 11.2, Politechnika Lubelska, Studia, semestr 5, Sem V, Sprawozdania, sprawozdania, Sprawozdania, L
Fiza 73 Nasza, 1 STUDIA - Informatyka Politechnika Koszalińska, finish, Fizyka, fiza, spr, fizyka, L
fizyka Hall, politechnika łódzka-technologia żywności, laboratoria z fizyki
FIZA 52 NASZA, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, Fizyka, fiza, spr, fizyka, La
więcej podobnych podstron