1. Zdarzenie losowe ![]()
- zb. Zdarzeń losowych
Aksjomat 1. - niepustość
Ω ![]()
Ω- jest zdarzeniem losowym
Aksjomat 2: komplementarność
A ![]()
→ ` = (Ω-A) ![]()
Aksjomat 3: -przeliczalnej addytymności
A1, A2, A3 ... ![]()
→ A1 ∨A2 ∨ A3 ∨ = (i=1υ∞ Ai ) ![]()
2.Prawdopodobieństwo to pewna funkcja określona na zbiorze zdarzeń l losowych o warosciach rzeczywistych
Aksjomat 1. - niepustość
Ω ![]()
Ω- jest zdarzeniem losowym
Aksjomat 2: komplementarność∨
A ![]()
→ ` = (Ω-A) ![]()
Aksjomat 3: -przeliczalnej addytymności
A1, A2, A3 ... ![]()
→ A1 ∨A2 ∨ A3 ∨ = (i=1υ∞ Ai ) ![]()
Aksjomat 4: A ![]()
→ P( >
Aksjomat 5: P(Ω) =1
Aksjomat 6: def. A.N.Kołmogorowa
Ai ∧ Aj ≠0 i ≠ j
P(A1 ∧ A2 ∧A3 ∧ ....)= P(A1) + P(A2) + P(A3) +...
3.Geometryczna def. Prawdopodobieństwa
Ω - jest tworem geometrycznym o skończonej mierze m
Zdarzenie losowe to każdy mierzalny podzbiór Ω. Prawdopodobieństwem zdarzenia A jest miara zbioru A miara zbioru Ω P(A)= m(A)/m(Ω)
4. Zmienna losowa X,Y X jest zmienną losową, gdy jest funkcją ![]()
mierzalną, określoną na zbiorze ![]()
o wartościach rzeczywistych![]()
→ R
![]()
mierzalna
![]()
zdarzenie elementarne
X(![]()
) - wartość funkcji X w punkcie ![]()
![]()
mierzalna - dla każdego x rzeczywistego, zbiór tych argumentów (![]()
), dla którego wartość funkcji jest mniejsza od x to musi należeć do zbioru ![]()
xR {![]()
: X(![]()
) < x } ![]()
ten zbiór musi być zdarzeniem losowym
5. Dystrybuanta - to funkcja F określona na zbiorze liczb rzeczywistych o wartościach rzeczywistych.
F, Fx : R → R F(x)=P({![]()
: X(![]()
) < x }) = P( X < x )
Właściwości:
- dla każdego X rzeczywistego, F(x) jest między 0 a 1
xR 0 ![]()
F(x) ![]()
1
- F(x) jest funkcją niemalejącą
jeżeli x1 < x2 ![]()
F(x1) ![]()
F(x2)
- Funkcja F(x) jest przynajmniej lewostronnie ciągła ( uwaga: jeśli w definicji zmiennej losowej przyjmiemy znak ![]()
to należy użyć słowa prawostronnie )
- lim x→ - F(x) = 0, lim x→ F(x) = 1
- x1<x2 P ( x1![]()
X < x2 ) = F(x2) - F(x1)
6. Typy zmiennych losowych
- dyskretne (skokowe)
- ciągłe - absolutnie ciągłe
- syngularne
7. Funkcja gęstości
![]()
Zmienna losowa X ma rozkład absolutnie ciągły jeśli istnieje nieujemna, całkowalna funkcja f(x) taka że dystrybuanta F(x) jest w postaci:
wykres jest linią ciągłą
f(x) - funkcja rozkładu gęstości rozkładu prawdopodobieństwa, częstotliwość występowania wartości X.
Szybkość zmiany dystrybuanty
f(x) to pochodna F'(x) wszędzie tam gdzie ta pochodna istnieje
f(x) = F'(x)
Lim x→ F(x) = 1
![]()
Limx→ =
=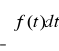
= 1
Twierdzenie: Jeżeli funkcja f(x) ![]()
0, jest całkowalna oraz 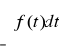
= 1 to istnieje ![]()
, ![]()
, P takie, że f(x) jest funkcją gęstości pewnej zmiennej losowej.
8. Wartość oczekiwalna
E[X] = EX Σ xi pi
∫ x f(x)dx
Własności wartości oczekiwanej
wartość oczekiwana od stałej = stałej
E(c)=C
wartość oczekiwana od cX = wartość oczekiwana
E(cX) = cEX
wartość oczekiwana sumy
E(X+Y) = EX + EY
wartość oczekiwana różnicy
E(X-Y) = EX - EY
wartość oczekiwana iloczynu
E(XY) = EX * EY jeżeli zmienne losowe są niezależne
wartość oczekiwana pewnej funkcji h
E[h(X)] = Σ h(xi)pi x - dyskretne
∫ h(x)f(x)dx dx - absolutnie ciągłe
Obliczanie wartości oczekiwanej dla rozkładu wykładniczego
f(x)= 0 x≤0
λe-λx x≥0
E(x) = 1/λ
Obliczenie wartości oczekiwanej dla rozkładu normalnego
Jeżeli X ma rozkład normalny N(μ,a), wartość oczekiwana EX = μ
Obliczanie wartości oczekiwanej dla rozkładu jednostajnego
0 x<a
f(x) = 1/(b-a) a≤x≤b
x>b
EX=-∞∫∞xf(s)dx=-∞∫ax0dx+a∫b(1/(b-a))dx+b∫∞x0dx=1/(b-a) a∫bxdx=
=(1/(b-a))(x2/2)ab=(1/2)(1/(b-a))(b2-a2)=((b-a)(b-a))/2(b-a)=(a+b)/2
9.Wariancje zmiennych losowych - kwadrat odchylenia (błędu)
- 2 moment zwykły
σ2=Var(X)=D2(X)=E(X-EX)2=E(X2) -(EX)2
- 1 moment zwykły
VarX=E[(X-EX)2]= Σi (xi-EX)2pi x - dyskretna zmienna losowa
∞∫∞ (x-EX)2f(x)dx x - absolutnie ciągła zm. los.
Własności:
VarX≥0
VarC=0
Var(cX)=c2VarX
Var(X+Y)=VarX+VarY
Var(aX+b)=a2VarX
Odchylenie standardowe zmiennej losowej σ
σdef=√VarX
Współczynnik zmienności
σ/EX=√VarX/EX (σ/EX*100%)
10.Próba statystyczna - podzbiór x - taki ciąg zmiennych losowych o tym samym składzie (dystrybuancie F(x))
Populacja generalna X- zbiór wszystkich elementów posiadających pewną cechę. Jest zmienną losową o ustalonej dystrybuancie
F(x)=P(X<x), x∈R
Założenia
próba musi być dostatecznie liczna :
mała n<30 (n≤30)
duża n≥30 (n>30)
próba musi być losowa
próba powinna być reprezentatywna
11.Estymacja wymaga:
zgodności estymatora
Qn jest zgodny z Q, jeśli dla każdego Ε>0 (l. Dodatnie)
lim P(|Qn-Q|≥E)=0
n→∞
żądanie nieobciążoności estymatora
E(Qn)=Q
efektywność estymatora Var(Qn)<Var(Q)
Estymacja punktowa
dla Q=EX x=1/nΣni=1 xi - zgodny, nieobciążony, najefektywniejszy
dla Q=VarX s2=1/nΣni=1 (xi-xi) - zgodny, obciążony
s2=s2=1/(n-1) Σni=1 (xi-x)2- zgodny, nieobciążony
12 Estymacja przedziałowa
(g1(α,Qn), g2 (α,Qn)) - przedział ufności
P(g1(α,Qn)<Q<g2(α.Qn)) = 1-α (1-α -współczynnik ufności)
Model I
X ma rozkład naormalny N (μ, τ), przy czym wartość oczekiwana μ jest nieznane, ale odchylenie standardowe τ jest znane. Przedział ufności wyznaczamy wzorem:
P(x+ μ α/2 τ/sqrt n < μ < x-μ 1-α/3 τ/sqrt n) =1-α
x - estym. Punkt. nieznanego parametru, μ α/2, μ1-α/2 - kwantyle rozkl. normal. N(0,1) odzczytywane z tablic przy czym μα/2 =μ1-α/2
Model II
X ma rozkład normalny N (μ, τ), przy czym wartość oczekiwania μ oraz odchylenie standardowe τ są nieznane. Dysponujemy małą próbą n≤30
Przedział ufności:
P(x+t α/2,n-1 S/sqrt n-1 < μ < x +t 1-α/2,n-1 S/sqrt n-1)=1-α
lub P(x+tα/2,n-1 S*/sqrt n < μ < x +t 1-α/2,n-1 S*/sqrt n)= 1-α
tα/2,n-1, t1-α/2,n-1 -kwantyle rozkładu t-studenta odczytywane z tablic przy czym tα/2,n-1 + t1-α/2,n-1=0
Model III
X ma rozkład normalny N((μ, τ) lub dowolny inny, przy czym wartość oczekiwana μ oraz odchylenie standardowe τ są nieznane. Dysponujemy dużą próbą n>30
P(x + μα/2 S/sqrt n < μ< x+μ1-α/2 S/sqrt n)=1-α
μα/2 , μ1-α/2 to kwantyle rozkładu normalnego N (0,1) odczytywane z tablic
13. Hipoteza statystyczna
To każde przypuszczenie dotyczące populacji X. Zawsze podajemy 2 hipotezy:
H0 - hipoteza, która będzie weryfikowana
H1 - hipoteza alternatywna (przeciwstawna)
Do weryfikacji hipotezy H0 uzywamy tzw testy statystyczne
Decyzja\Ho prawdziwa fałszywa
uznaćHo decyzja słuszna błąd II rodzaju β
nie uznaćHo błąd I rodzajuα decyzja słuszna
Algorytmy są tak dopasowane aby zminimalizować błąd β. Sposób postępowania:
postepowanie 2 hipotez (Ho i H1)
ustalenie poziomu istotności α
wyliczenie na podstawie wykonanej próby losowej wartości statystyki testującej
ustalenie tzw obszaru krytycznego Rα
podjęcie decyzji - jeśli wartość statyst. testującej należy do obszaru krytycznego to Ho odrzucamy zaznaczając za prawdziwą H1(ryzyko niesłusznego odrzucenia Ho wynosi α). Jeśli wartość statyst. testującej nie należy do obszaru krytycznego to mowimy że nasze obserwacje są niesprzeczne z Ho (co nie musi oznaczac jej prawdziwosci)
14 Test dla wartości średniej
Model I
X ma rozkład normalny N(μ, τ),μ- nieznane, τ- znane
H0: μ=m0
H1: (a) μ≠m0, (b) μ< m0, (c) μ>m0
Statystyka testująca: μ = (x- m0)/ τ sqrt n n-ilość elementów próby; m0 konkretna, hipotetyczna wartość
Rα=(-∞,μα/2]∪[ μ1-α/2, ∞)
Rα=(-∞,μα/2]
Rα=[μ1-α/2, ∞)
Model II
X ma rozkład normalny N(μ, τ), μ, τ- nieznane, mała próba n<30
H0: μ=m0
H1: (a) μ≠m0, (b) μ< m0, (c) μ>m0
Statystyka testująca: t = (x- m0)/ S sqrt n-1=(x- m0)/ S sqrt n
Rα=(-∞, tα/2,n-1] ∪[t1-α/2, n-1, ∞)
Rα=(-∞, tα/2,n-1]
[t1-α/2, n-1, ∞)
TEST DLA DWÓCH ŚREDNICH
Model III
Badamy 2populacje o rozkładzie normalnym N(µ1, δ i N(µ2, δ, µ1i µ2 są nieznane, ale δ =δ Dysponujemy wynikami 2niezależnych małych prób o ilościach n1 i n2.
H0: µ1= µ2
H2: (a) µ1 µ2 , (b) µ1 µ2, (c) µ1> µ2
![]()
Statystyka test.
(a) ![]()
(b) ![]()
(c) ![]()
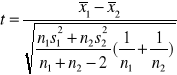
Wyszukiwarka
Podobne podstrony:
IP - test (zestaw 07), Studia UMK FiR, Licencjat, II rok - moduł Rachunkowość, Ochrona własności int
Dobre estymatory wartości oczekiwanej 2
Tablica standaryzowanego rozkładu normalnego o wartości oczekiwanej równej zeru i wariancji równej j
statystyka, Przedzial ufnosci dla m. Testowanie hipotezy dla m., PRZEDZIAŁ UFNOŚCI DLA WARTOŚCI OCZE
IP - test (zestaw 11), Studia UMK FiR, Licencjat, II rok - moduł Rachunkowość, Ochrona własności int
IP - test (zestaw 08), Studia UMK FiR, Licencjat, II rok - moduł Rachunkowość, Ochrona własności int
OWI SKRYPT, Finanse i rachunkowość, Ochrona własności intelektualnej
IP - test (zestaw 03), Studia UMK FiR, Licencjat, II rok - moduł Rachunkowość, Ochrona własności int
479 Wyklad 2 rachunek kosztow 2 utrata wartosci aktywow
IP - test (zestaw 12), Studia UMK FiR, Licencjat, II rok - moduł Rachunkowość, Ochrona własności int
IP - test (zestaw 04), Studia UMK FiR, Licencjat, II rok - moduł Rachunkowość, Ochrona własności int
owi-nasz-test, Studia UMK FiR, Licencjat, II rok - moduł Rachunkowość, Ochrona własności intelektual
ściąga odchylenie i wartość oczekiwana
Rachunkowość bankowa- Papiery wartościowe, wykład 4
IP - test (zestaw 02), Studia UMK FiR, Licencjat, II rok - moduł Rachunkowość, Ochrona własności int
więcej podobnych podstron