P O L I T E C H N I K A Ś W I Ę T O K R Z Y S K A LABORATORIUM AUTOMATYKI
|
||||||
Ćwiczenie nr: 2 |
Temat : WYZNACZENIE ODPOWIEDZI SKOKOWEJ UKŁADU BĘDĄCEGO POŁĄCZENIEM SZEREGOWYCH CZŁONÓW CAŁKUJĄCEGO I OSCYLACYJNEGO |
|||||
1999/2000 Rok akadem. |
V Semestr. |
32B Grupa. |
Tor Piotr Purtak Michał
Nazwisko i imię studenta |
99-12-12 Data. |
Ocena. |
|
Wstęp teoretyczny.
Element całkujący.
Elementem całkującym nazywamy obiekt dynamiczny opisany równaniem różniczkowym w postaci:
![]()
gdzie k oznacza współczynnik wzmocnienia określony jako stosunek pochodnej odpowiedzi do wymuszenia w stanie ustalonym. Stosując odpowiednie przekształcenia otrzymujemy transmitancję: ![]()
oraz odpowiedź jednostkową h(t) = k . t, przedstawiona na rysunku poniżej.
Odpowiedź jednostkowa elementu całkującego
Element oscylacyjny.
Równanie różniczkowe opisujące zachowanie się elementu oscylacyjnego ma postać:
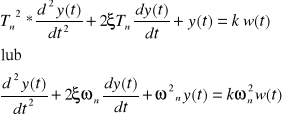
gdzie:
k - współczynnik wzmocnienia w stanie ustalonym,
![]()
pulsacja drgań własnych nietłumionych - naturalna,
![]()
względny / zredukowany / współczynnik tłumienia , ![]()
Dokonując transformacji Laplace”a powyższego równania obliczamy transmitancją operatorową :
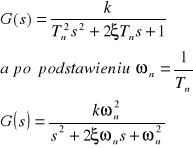
Charakterystykę jednostkową rozpatrywanego elementu określa zależność:
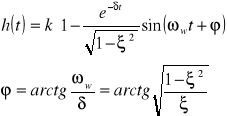
Rys. Odpowiedź jednostkowa elementu oscylacyjnego.
Połączenie szeregowe.
![]()
Przebieg ćwiczenia.
Wyznaczyć odpowiedź skokową układu będącego połączeniem szeregowym członów :
całkującego (Tc=1[s])
oscylacyjnego II rzędu (k =1; T = 0,1 [s]; ξ = 0,1)
Równania różniczkowe i transmitancje członów;
całkującego
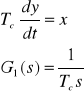
oscylacyjnego II rzędu;
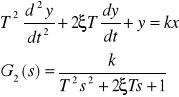
Transmitancja zastępcza dla połączenia szeregowego:
![]()
Po przekształceniu i podaniu równania przekształceniu odwrotnemu LAPLACE”A otrzymuje równanie różniczkowe:
![]()
po podstawieniu wartości;
![]()
y(t)
t
α
tgα = k
Rys. 1.1. Oznaczenie elementu całkującego na schematach blokowych.
Wyszukiwarka
Podobne podstrony:
cw4 Zespół Klinefeltera
OS gr03 cw4 id 340946 Nieznany
cw4 badanie drgan skretnych
crossgosp, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 3, SEMESTR V, Woi
postępowanie cywilne-ćw4, pomoce naukowe ;), Postępowanie cywilne
PTK cw4, WAT, SEMESTR II, PTK
ćw4 8 11
cw4 protokol
cw4 telex cz1 id 123468 Nieznany
cw4
inventor cw4 zespol
Cw4 tow
CW4 doc
Makroekonomia cw4
GrzeszykAnna I0I1S1 cw4 spr
Cw4 odp id 123443 Nieznany
cw4 korozja 2 id 123441 Nieznany
Inventor cw4 zespol
więcej podobnych podstron