Rok studiów: pierwszy	Nazwisko i imię: Krupa Michał	Rok akademicki: 2000/2001
Numer ćwiczenia: 11	Temat: Sprawdzanie II zasady dynamiki dla ruchu obrotowego	Nazwisko prowadzącego: Prof. Czesław Kajtoch
Data rozpoczęcia ćwiczenia: Data zakończenia ćwiczenia: Data oddania sprawozdania:		Ocena końcowa:

Cele ćwiczenia

Doświadczalne sprawdzenie twierdzenia Steinera oraz sprawdzenie zależności  (M) przy stałych momentach bezwładności.

Wstęp teoretyczny

Ruch obrotowy odbywa się wokół ustalonej osi. Gdy bryła obraca się wokół stałej osi to droga, prędkość i przyspieszenie liniowe każdego z jej punktów zależą od odległości od tej osi, wszystkie jednak punkty bryły przebywają taką samą drogę. Mają taką samą prędkość i przyspieszenie kątowe.

Druga zasada dynamiki dla ruchu obrotowego:

M - Moment sił wypadkowych działających na ciało,

I -Moment bezwładności

W ćwiczeniu tym korzystać będziemy ze wzorów:

opisujących spadek swobodny ciał ,

h- droga,

a- przyśpieszenie liniowe,

t- czas

związek między przyśpieszeniem kątowym, a liniowym,

a=r,

- przyśpieszenie kątowe

r- promień tulei łożyska osi obrotu.

Po przekształceniu otrzymamy:

,

Moment siły obliczamy ze wzoru:

M=mgr,

Twierdzenie Steinera mówi, że moment bezwładności względem osi O' jest równy sumie momentu bezwładności względem równoległej do niej osi O przechodzącej przez środek masy bryły i kwadratu odległości między obiema osiami.

Cele ćwiczenia.

Doskonalenie umiejętności pomiarów długości, czasu, masy, planowanie pomiarów końcowych, sprawdzanie II zasady dynamiki przez wykreślenie graficznie zależności ε(M), przy stałych momentach bezwładności, oraz doświadczalne sprawdzenie twierdzenia Steinera.

TOK POSTĘPOWANIA

Należy ustawić wahadło, wyznaczamy masę krążków m. i masy obciążników oraz trzy wartości promieni. Wyznaczamy ruchy obciążników odległe o h, wykonujemy 4 serie pomiarów: bez krążków, krążki jak najbliżej osi obrotu, krążki w środkowym położeniu, oraz krążki maksymalnie odsunięte od osi obrotu, wyniki umieszczamy w tabelce i określamy zależność ε(M) przy I = const. Następnie z wykresów wyznaczamy momenty bezwładności, dla wybranego momentu siły przeprowadzamy pomiary w zależności od momentu bezwładności krzyża. Wyniki umieszczamy w tabeli i wykonujemy wykres ε(I^-1). Tangens nachylenia otrzymanej prostej powinien być równy zadanemu momentowi siły, co sprawdzamy z danymi w tabeli.

Opracowanie wyników.

Niepewność pomiarową obliczamy metodą różniczki zupełnej:

Dla przyśpieszenia kątowego:

Dla momentu siły:

M=mgr

Dla poszczególnych momentów bezwładności:

,

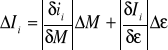
Pomiar 1

	m [kg]	t1 [s]	t2 [s]	tśr [s]	M [Nm]	 [s^-2]	I [kgm^2]
1	0,1495	8,74	8,65	8,695	0,01100	2,43377	0,00452
2	0,2999	6,12	6,1	6,11	0,02206	4,92873	0,00448
3	0,3499	5,07	5,25	5,16	0,02574	6,91064	0,00372
4	0,5998	4,35	4,31	4,33	0,04412	9,81391	0,00450

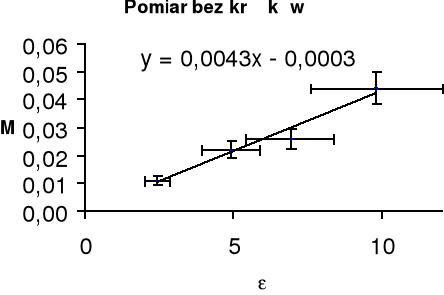
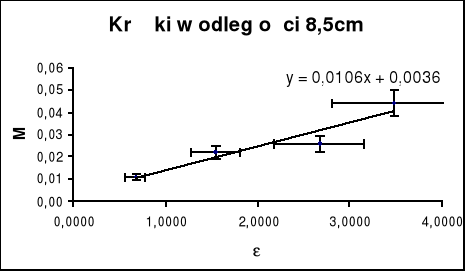
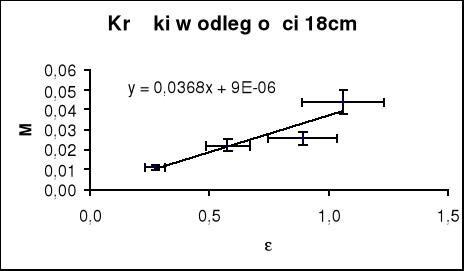
Współczynnik kierunkowy wykresu względem pierwszej osi (tangens tego kąta jest szukaną przez nas wartością

	m [kg]	Procentowy udział	t [s]	Procentowy udział	r [m]	Procentowy udział	h [m]	Procentowy udział	M [Nm]	 [s^-2]	I [kgm^2]	I I
1	0,0001	0,02%	0,2	14,61%	0,001	84,71%	0,001	0,92%	0,0015	0,4400	0,0014	31,48%
2	0,0001	0,02%	0,2	19,61%	0,001	79,86%	0,001	0,87%	0,0029	0,9870	0,0015	33,39%
3	0,0001	0,02%	0,2	22,41%	0,001	77,09%	0,001	0,84%	0,0034	1,4671	0,0013	34,59%
4	0,0001	0,01%	0,2	25,61%	0,001	73,94%	0,001	0,80%	0,0059	2,2293	0,0016	36,07%

Uzyskaliśmy w ten sposób I₀, które możemy podstawić do wzoru opisującego twierdzenie Steinera.

Pomiar 2

	M [kg]	t1 [s]	t2 [s]	tśr [s]	M [Nm]	 [s^-2]	I [kgm^2]
1	0,1495	9,84	9,91	9,875	0,0110	1,8869	0,0058
2	0,2999	6,63	6,68	6,655	0,0221	4,1545	0,0053
3	0,3499	5,18	5,2	5,19	0,0257	6,8310	0,0038
4	0,5998	4,28	4,2	4,24	0,0441	10,2350	0,0043

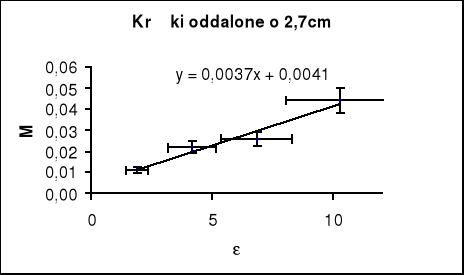
Sprawdzimy teraz prawdziwość twierdzenia Steinera dla tego pomiaru.

m - masa krążków

R₁ - odległość krążków od osi obrotu

Niepewność pomiarowa natomiast:

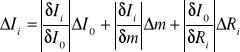
, dla i={1,2,3}

	m [kg]	Procentowy udział	t [s]	Procentowy udział	r [m]	Procentowy udział	h [m]	Procentowy udział	M [Nm]	 [s^-2]	I [kgm^2]	I I
1	0,0001	0,02%	0,2	13,10%	0,001	86,22%	0,001	0,94%	0,0015	0,3307	0,0018	30,93%
2	0,0001	0,02%	0,2	18,29%	0,001	81,16%	0,001	0,88%	0,0029	0,8097	0,0017	32,86%
3	0,0001	0,02%	0,2	22,31%	0,001	77,19%	0,001	0,84%	0,0034	1,4472	0,0013	34,55%
4	0,0001	0,01%	0,2	26,02%	0,001	73,54%	0,001	0,80%	0,0059	2,3451	0,0016	36,26%

Pomiar 3

	m [kg]	t1 [s]	t2 [s]	tśr [s]	M [Nm]	 [s^-2]	I [kgm^2]
1	0,1495	16,52	16,5	16,51	0,0110	0,6750	0,0163
2	0,2999	10,95	10,91	10,93	0,0221	1,5402	0,0143
3	0,3499	8,29	8,31	8,3	0,0257	2,6709	0,0096
4	0,5998	7,29	7,26	7,275	0,0441	3,4766	0,0127

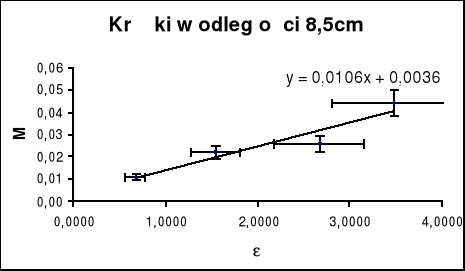
m - masa krążków

R₂ - odległość krążków od osi obrotu

	m [kg]	Procentowy udział	t [s]	Procentowy udział	r [m]	Procentowy udział	h [m]	Procentowy udział	M [Nm]	 [s^-2]	I [kgm^2]	I I
1	0,0001	0,01%	0,2	8,27%	0,001	91,01%	0,001	0,99%	0,0015	0,1073	0,0048	29,30%
2	0,0001	0,01%	0,2	12,00%	0,001	87,42%	0,001	0,95%	0,0029	0,2640	0,0044	30,50%
3	0,0001	0,01%	0,2	15,22%	0,001	84,23%	0,001	0,92%	0,0034	0,4887	0,0031	31,66%
4	0,0001	0,01%	0,2	17,01%	0,001	82,49%	0,001	0,90%	0,0059	0,6597	0,0041	32,33%

Pomiar 4

	m [kg]	t1 [s]	t2 [s]	tśr [s]	M [Nm]	 [s^-2]	I [kgm^2]
1	0,1495	0,001	25,93	26,01	0,0110	0,2720	0,0404
2	0,2999	0,001	17,87	17,88	0,0221	0,5755	0,0383
3	0,3499	0,001	14,35	14,39	0,0257	0,8886	0,0290
4	0,5998	0,001	13,15	13,18	0,0441	1,0592	0,0416

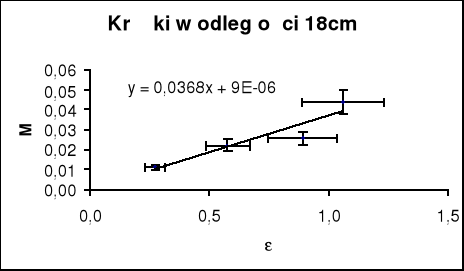
m - masa krążków

R₃ - odległość krążków od osi obrotu

	m [kg]	Procentowy udział	t [s]	Procentowy udział	r [m]	Procentowy udział	h [m]	Procentowy udział	M [Nm]	 [s^-2]	I [kgm^2]	I I
1	0,0001	0,01%	0,2	5,41%	0,001	93,84%	0,001	1,02%	0,0015	0,0408	0,0115	28,42%
2	0,0001	0,01%	0,2	7,69%	0,001	91,69%	0,001	1,00%	0,0029	0,0904	0,0111	29,08%
3	0,0001	0,01%	0,2	9,38%	0,001	90,03%	0,001	0,98%	0,0034	0,1445	0,0086	29,62%
4	0,0001	0,00%	0,2	10,16%	0,001	89,30%	0,001	0,97%	0,0059	0,1749	0,0124	29,86%

Wnioski.

Nie udało się potwierdzić prawdziwości twierdzenia Steinera w doświadczeniu z wahadłem Oberbecka. Spowodowane jest to zbyt dużą niepewnością pomiarową i mimo iż niektóre wyniki mieszczą się w granicach niepewności to jednak jest to zbyt duży rozrzut aby móc przyjąć te wyniki jako pewne. Największą niepewność pomiarową dawał promień tulei, ok. 90% oraz pomiar czasu co musiało wpłynąć ujemnie na uzyskane wyniki. Niepewność pomiarowa dla I wynosi ok. 34% uzyskanej wartości. Chcąc uzyskać mniejszą niepewność pomiarową należałoby zoptymalizować doświadczenie względem właśnie tego promienia.

---