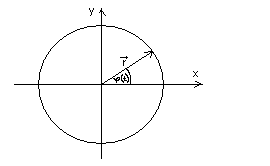
3 Dowolny ruch po okręgu koła.

Układ Kartezjański. Układ biegunowy.

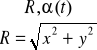
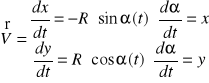
Prędkość kątowa -

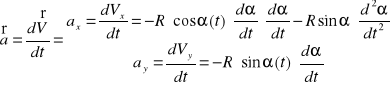
Przyśpieszenie kątowe:

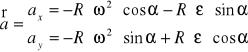
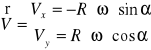
Gdy ruch jest jednostajny po okręgu koła, to: w-const.,

Okres ruchu:
częstotliwość ruchu: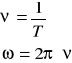

Wektor prędkości kątowej:

w musi być takie, aby

• 
  

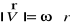
• kierunek zgodny (
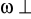
  do płaszcz. ruchu)

• zgodny zwrot taki aby wektory w, r, V tworzyły trójkę prawoskrętną

04 Zasady dynamiki Newtona.

Podstawowa teoria, która pozwala przewidywać ruch ciał, składa się z trzech równań, które nazywają się zasadami dynamiki Newtona.

Sformułowanie pierwszej zasady dynamiki Newtona:

Ciało, na które nie działa żadna siła (lub gdy siła wypadkowa jest równa zeru) pozostaje w spoczynku lub porusza się ze stałą prędkością po linii prostej.

   Siła wypadkowa F_wyp jest sumą wektorową wszystkich sił działających na ciało. Jeżeli F_wyp = 0 to również przyspieszenie ciała a = 0, a to oznacza, że nie zmienia się ani wartość ani kierunek prędkości tzn. ciało jest w stanie spoczynku lub porusza się ze stałą co do wartości prędkością po linii prostej.   Zgodnie z pierwszą zasadą dynamiki nie ma rozróżnienia między ciałami spoczywającymi i poruszającymi się ze stałą prędkością. Nie ma też różnicy pomiędzy sytuacją gdy nie działa żadna siła i przypadkiem gdy wypadkowa wszystkich sił jest równa zeru.

Sformułowanie drugiej zasady dynamiki Newtona:

Tempo zmian pędu ciała jest równe sile wypadkowej działającej na to ciało. Dla ciała o stałej masie sprowadza się to do iloczynu masy i przyspieszenia ciała.

  lub 

Sformułowanie trzeciej zasady dynamiki Newtona:

Gdy dwa ciała oddziałują wzajemnie, to siła wywierana przez ciało drugie na ciało pierwsze jest równa i przeciwnie skierowana do siły, jaką ciało pierwsze działa na drugie.

Pierwsza zasada dynamiki wydaje się być szczególnym przypadkiem drugiej bo gdy a = 0 to i F_wyp = 0 . Przypisujemy jej jednak wielką wagę dlatego, że zawiera ważne pojęcie fizyczne: definicję inercjalnego układu odniesienia. Pierwsza zasada dynamiki stwierdza, że jeżeli na ciało nie działa żadna siła (lub gdy siła wypadkowa jest równa zeru) to istnieje taki układ odniesienia, w którym to ciało spoczywa lub porusza się ruchem jednostajnym prostoliniowym. Taki układ nazywamy układem inercjalnym.

5. Przykłady całkowania równań Newtona. Ruch pod wpływem siły lepkości wiskotycznej.

Przykłady całkowania równań Newtona.

Przykład 1:

Wektorowe równanie ruchu dla siły zależnej od czasu
lub
ma postać:

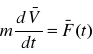
z warunkami początkowymi t = t₀,
,
można to równanie zapisać jako układ trzech równań skalarnych:

i = x, y, z

przekształcamy i całkujemy powyższe równania

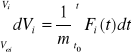
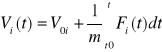
Z definicji prędkości mamy: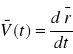
, rozdzielamy zmienne i całkujemy

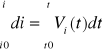
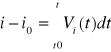
Przykład 2:

Wykonujemy rzut ukośny ciała o masie m z wysokości h. Zaniedbujemy opory powietrza i inne głupoty. Obliczamy zasięg rzutu.

Siła ciężkości (jedyna siłą działająca na ciało)
, równanie ruchu ma więc postać:

warunki początkowe w czasie t = 0

r(0) = (0,h), V(0)= (V₁, V₂)

Ruch odbywa się na płaszczyźnie xy, więc zapisujemy 2 równania ruchu:

Całkujemy w granicach określonych przez warunki początkowe

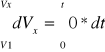
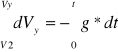
Otrzymujemy wyrażenie na składowe prędkości:

V_x - V₁ = 0 V_y - V₂ = -g*t

Z definicji prędkości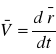
dostajemy równania, z których liczymy współrzędne x oraz y.

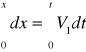
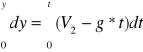
otrzymujemy

x = V₁*t

Ciało upada na ziemię jeśli y=0, mamy więc wzór na odległość, jaką przeleci zanim padnie:

Ruch pod wpływem siły lepkości wiskotycznej

Lepkość - czyli tarcie wewnętrzne, jest to właściwość ciał stałych, cieczy, ciekłych kryształów, gazów lub plazmy.

Lepkość wiskotyczna - wartość siły lepkości zależy od prędkości.

Dla niewielkich prędkości w wielu sytuacjach siłę oporu wiskotycznego można wyrazić wzorem
, gdzie b = const >0. Równanie ruchu w takim przypadku przyjmuje postać:

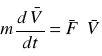
Dla większych prędkości siła oporu jest proporcjonalna do kwadratu prędkości F= -bV²

Przykład: Kulka wrzucona do cieczy

Na kulkę działają siły:

- oporu wiskotycznego

- wyporu cieczy

- ciężar

Ruch kulki odbywa się pod wpływem wypadkowej siły:

6. Praca, moc, energia kinetyczna, energia potencjalna

Praca

Praca elementarna - iloczyn skalarny wektora siły F i wektora elementarnego przemieszczenia:

Na takim przemieszczeniu siłę możemy traktować jako stałą, zatem praca elementarna wynosi:
, gdzie alfa = kąt między wektorami F i dr, F_s - składowa styczna siły, ds =|dr| - elementarna droga.

Jednostką pracy jest dżul 1J = 1N* 1m

Siła prostopadła do przemieszczenia nie wykonuje pracy (praca = 0) np. satelita krążący nad Ziemią na stałej wysokości nie wykonuje pracy (siły grawitacyjne nie wykonują pracy).

Praca jest dodatnia dla ostrych kątów alfa, ale dla alfa = (90, 180> przyjmuje wartości ujemne.

Praca siły F na skończonym przemieszczeniu między punktami A i B wyraża się całką krzywoliniową:

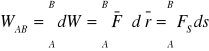
W układzie kartezjańskim całka ta przyjmuje postać: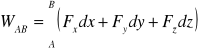

Moc

Przy podnoszeniu danego ciała na określoną wysokość trzeba zawsze wykonać taką samą pracę niezależnie od tego, ile ta czynność trwała. Często dużo bardziej interesuje nas szybkość wykonania pracy niż całkowita wykonana praca. Szybkość wykonywania pracy nazywamy mocą. Średnia moc dostarczana przez jakieś urządzenie równa jest całkowitej dostarczonej mocy podzielonej przez czas jej wykonywania.

Moc chwilowa dana jest wzorem:

Gdy moc jest stała w czasie zachodzi związek: W= P*t

Jednostką mocy w układzie SI jest Wat W = J/s, ale często używaną jest także koń mechaniczny KM równy mocy jaką może wydatkować koń. 1 KM ≈ 736 W.

Pracę można także wyrazić jako iloczyn mocy i czasu. Stąd pochodzi powszechnie używana jednostka, kilowatogodzina [kWh]. Kilowatogodzina to praca, jaką wykona urządzenie o mocy 1W w czasie 1h.

Energia kinetyczna

Stan mechaniczny cząstki określają 2 wielkości: wektor położenia r(t) i wektor prędkości V(t), zwane parametrami stanu. Każdą funkcję zależną tylko od r(t) i V(t) nazywamy funkcją stanu. Zmiana stanu mechanicznego cząstki, a więc zmiana jej położenia lub prędkości wymaga na ogół wykonania pracy. Praca elementarna wynosi:

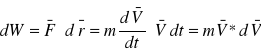
Praca potrzebna na zwiększenie prędkości cząstki o masie m z prędkości do V_A do V_B. Zakładamy, że masa ciała nie zmienia się w czasie ruchu.

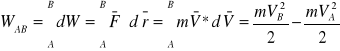
Wartość otrzymana po prawej stronie
zależy tylko od prędkości, jest więc funkcją stanu. Wartość na nosi nazwę energii kinetycznej. Energia kinetyczna jest zawsze nieujemna: dodatnia dla poruszającej się i 0 dla spoczywającej. Zmiana energii kinetycznej równa jest pracy wykonanej przez siły rozpędzające lub hamujące cząstkę:
Dla dodatnich wartości tej pracy E_k rośnie, dla ujemnych - maleje. Energia kinetyczna równa jest pracy, jaką może wykonać to ciało, zanim się zatrzyma.

Energia potencjalna

Podczas podnoszenia ciała zmienia się stan mechaniczny cząstki, ale energia kinetyczna pozostaje taka sama. Wykonana praca jest wówczas równa zmianie energii potencjalnej, która jest funkcją stanu.

Jeśli siła F jest siłą zachowawczą będącą jedynie funkcją położenia ciała, tzn.
oraz praca wykonana przez tę siłę przy przemieszczeniu cząstki o wektor
da się wyrazić w postaci:
, E_p jest jednoznaczną funkcją skalarną położenia
, ciągłą i mającą ciągłe pochodne, niezależną od czasu, to funkcję stanu
nazywamy energią potencjalną ciała w położeniu
, w polu siły zachowawczej
.

Zmiana energii potencjalnej
jest równa ujemnej pracy wykonanej przez siłę zachowawczą przy zmianie położenia cząstki z punktu A do B:

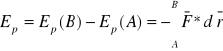
Zwykle przyjmuje się pewien punkt przestrzeni A jako punkt odniesienia i wyznacza różnice E_p względem tego punktu. W dowolnym punkcie P:

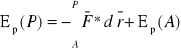
Najczęściej stosujemy wyrażenie na grawitacyjną energię potencjalną na wysokości h względem powierzchni Ziemi, zakładając że siła pola grawitacyjnego wynosi

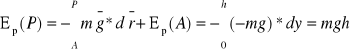
Obliczając E_P(P) względem punktu A, który leży na powierzchni Ziemi (współrzędna y = 0) przyjęliśmy E_P(A) = 0. Uzyskany wzór jest prawdziwy tylko dla niewielkich wysokości ponad powierzchnią Ziemi.

W przypadku ogólnym grawitacyjna energia potencjalna równa jest ujemnej pracy wykonanej przez siły pola grawitacyjnego
podczas przesunięcia cząstki z punktu A, znajdującego się w nieskończoności, dla którego przyjmujemy
dla danego punktu P, będącego naszym punktem odniesienia

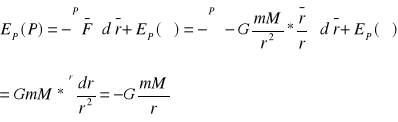
9. Zasada zachowania momentu pędu dla układu punktów materialnych

Pęd układu - Przypuszczamy, że mamy układ „n” punktów materialnych o masie m1,m2..Zakładamy, że substancja ani nie dopływa ani nie odpływa z układu (M=const) Każdy punkt będzie miał w takim przypadku pęd: p1=m1*v1. Układ jako całość będzie miał całkowity pęd „P” zdefiniowany jako suma geometryczna pędów poszczególnych punktów materialnych. (P=p1+p2+p3…) Inaczej można powiedzieć, że całkowity pęd układu punktów materialnych jest równy iloczynowi całkowitej masy układu i prędkości jego środka masy. (P=M*v_śr.m)[1].
Z II zasady dynamiki Newtona mamy F_zew=M*a_śr.m [2] Różniczkując równanie [1] i [2] względem czasu, zakładając że masa nie ulega zmianie, otrzymamy: dP/dt=M*dv_śr.m /dt Pozwala nam to zapisać II Zasadę dynamiki w postaci F_zew= dP/dt [3]

Zasada zachowania pędu - Przypuszczamy, że suma zewnętrznych sił działających na układ jest równa zeru. Wtedy na podstawie równania [3] dP/dt =0 lub P = const Jeżeli wypadkowa sił działających na układ jest równa zeru, to całkowity wektor pędu tego układu pozostaje stały. Całkowity pęd układu może być zmieniony tylko przez siły zewnętrzne! Pędy poszczególnych punktów mogą ulegać zmianom, ale suma tych pędów, jeżeli na układ nie działa siła zewnętrzna, jest stała!

Ruch środka masy - środek masy porusza się tak jakby umieszczono w nim całą masę układu i przyłożono do niego sumę sił zewnętrznych układu.

10. Układy Inercjalne, Transformacje Galileusza, Zasada względności Galileusza

Układ inercjalny - Układ odniesienia związany z ciałem poruszającym się ruchem jednostajnie prostoliniowym, tj gdy v(t) = const, nazywamy inercjalnym układem odniesienia. Poszczególne inercjalne układy poruszają się względem siebie ruchem jednostajnym i prostoliniowym. Często przyjmuje się, że Ziemia jest układem inercjalnym lub zakłada się istnienie tzw gwiazd stałych!

Transformacje Galilusza

Zakładamy, że mamy układy inercjalne poruszające się względem siebie. W chwili t w punkcie P zachodzi zjawisko fizyczne, które nazwiemy zdarzeniem. W układzie S obserwator opisze to zjawisko współrzędnymi x, y, z Natomiast obserwator w układzie S' poruszającym się z prędkością u względem S, opisze to zdarzenie współrzędnymi x', y', z'
Transformacja Galileusza wiążąca ze sobą współrzędne zdarzenia w obu układach:

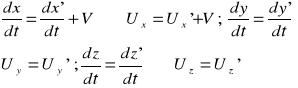
Czas w obu układach płynie tak samo: t' = t ; Transformacja przyspieszenia:

Zasada względności Galileusza - Prawa mechaniki muszą być takie same we wszystkich inercjalnych układach odniesienia, czyli są niezmienne względem transformacji Galileusza.

Uwagi: Nie da się stwierdzić doświadczalnie czy ukł. się porusza ruchem jednostajnym czy stoi (względem innego ukł. odniesienia)

---