11.Transformacje lorentza,

12. Zasada względności Einsteina

Tam gdzie napisane, że z zeszytu to jest z wykładów, tam gdzie nie jest nic napisane to z wykładów keczupa copy/paste. Nie wiem czy nie za dużo tego dałem. Ale tak łatwiej zrozumieć.

Źródło zeszyt{

Zasada względności Einsteina:

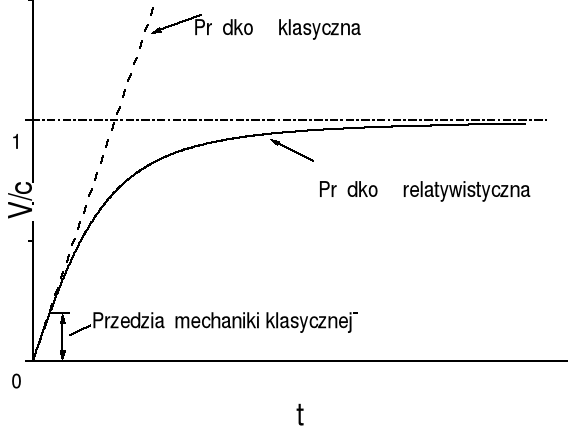
1. Istnieje maksymalna prędkość rozchodzenia się oddziaływań w przyrodzie równa c.

2. Prawa Przyrody (nie tylko mechaniki) mają jednakową postać we wszystkich inercjalnych układach odniesień. Maksymalna prędkość rozchodzenia się oddziaływań jest we wszystkich układach odniesienia „c”.

}

Einstein pokazał, że zasada zachowania energii jest spełniona w mechanice relatywistycznej pod warunkiem, że pomiędzy masą i całkowitą energią ciała zachodzi związek

(11.11)

To znane powszechnie równanie Einsteina opisuje równoważność masy i energii. Wynika z niego, że ciało w spoczynku ma zawsze pewną energię związaną z jego masa spoczynkową

Transformacje Lorentza

Szukamy ponownie (jak w przypadku transformacji Galileusza) wzorów przekładających spostrzeżenia jednego obserwatora na obserwacje drugiego. Chcemy znaleźć transformację współrzędnych ale taką, w której obiekt poruszający się z prędkością równą c w układzie nieruchomym (x, y, z, t), również w układzie (x', y', z', t') poruszającym się z prędkością V wzdłuż osi x będzie poruszać się z prędkością c.

Transformacja współrzędnych, która uwzględnia niezależność prędkości światła od układu odniesienia ma postać

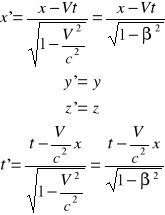
(11.3)

gdzie β = V/c. Te równania noszą nazwę transformacji Lorentza.

Omówimy teraz niektóre wnioski wynikające z transformacji Lorentza.

Przyjmijmy, że według obserwatora w rakiecie poruszającej się wzdłuż osi x' (czyli także wzdłuż osi x, bo zakładamy, *e te osie s* równoległe) pewne dwa zdarzenia zachodzą równocześnie Δt' = t₂' - t₁' = 0, ale w rożnych miejscach x₂' - x₁' = Δx' ≠ 0. Sprawdźmy, czy te same zdarzanie są również jednoczesne dla obserwatora w spoczynku. Z transformacji Lorentza wynika, że

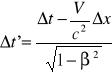
Łącząc oba powyższe równania otrzymujemy związek

(11.4)

Jeżeli teraz uwzględnimy fakt, że zdarzenia w układzie związanym z rakietą są jednoczesne Δt' = 0 to otrzymamy ostatecznie

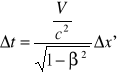
(11.5)

Widzimy, że równoczesność zdarzeń nie jest bezwzględna, w układzie nieruchomym te dwa zdarzenia nie są jednoczesne.

Skrócenie długości

Teraz rozpatrzmy inny przykład. W rakiecie poruszającej się z prędkością V, wzdłuż osi x' leży pręt o długości L'. Sprawdźmy jaką d*ugość tego pręta zaobserwuje obserwator w układzie nieruchomym.

Pomiar d*ugości pręta polega na zarejestrowaniu dwóch zjawisk zachodzących równocześnie na końcach pręta (np. zapalenie się żarówek). Ponieważ żarówki zapalają się na końcach pręta to Δx' = L'. Ponadto żarówki zapalają się w tym samym czasie (dla obserwatora w układzie spoczywającym ) to dodatkowo Δt = 0. Uwzględniając te warunki otrzymujemy na podstawie transformacji Lorentza

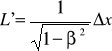
x jest długością pręta L w układzie nieruchomym więc

Okazuje się, że pręt ma mniejszą d*ugość, jest krótszy.

Źródło zeszyt {

Warunki jakie muszą spełniać transformacje lorentza:

1. Nie zmiennicze względem odwrócenia przy zamianie V-> -V to transformacje muszą być takie same

2. Jeżeli jakieś zdarzenie zaszło w pierwszym układzie w „skończoności” to musi zajść w skończoności w układzie.

3. Prędkość światła w obu układach jest jednakowa i równa „c”.}

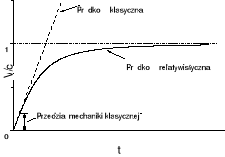
14 Dynamika relatywistyczna.

Pęd cząstki o masie własnej
:

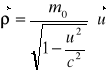
E to całkowita energia relatywistyczna cząstki swobodnej: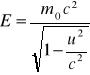

Transformacja Lorentz'a dla pędu-energii: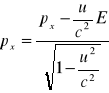
;

;

;

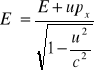
Zatem
to energia spoczynkowa cząstki. (bo
).

Definicja masy relatywistycznej: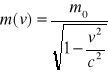

Relatywistyczna energia kinetyczna: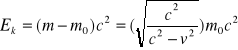

Jeżeli masa spoczynkowa układu zmniejsza się o
to wyzwala się energia:

Siła relatywistyczna jest pochodną pędu relatywistycznego względem czasu własnego obserwatora:

W układzie
na cząstkę działa siła:
i w układzie
poruszającym się względem
ta cząstka ma (chwilowo) prędkość 0, to:
,

,

.

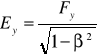
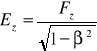
15. Energia kinetyczna i całkowita w teorii względności.

Związek pędu z energią.

W klasycznej dynamice przyjmuje się, że masa ciała jest niezależna od jego prędkości, tj. jest jednakowa we wszystkich układach odniesienia. Pęd i energia kinetyczna ciała poruszającego się z prędkością v określają wzory: p = mv,
Znaczenie pojęć pędu i energii kinetycznej w mechanice wynika m.in. z faktu, że dla układu ciał spełnione są w określonych warunkach prawa zachowania pędu i energii: jeżeli na ciała nie działają zewnętrzne siły, to całkowity pęd układu jest stałą wielkością, niezależną od czasu — podobnie jak całkowita energia układu.

ELEMENTY DYNAMIKI RELATYWISTYCZNEJ W codziennie spotykanych zjawiskach zmiana masy ciał, związana ze zmianą ich energii jest niezauważalna. W przypadku zjawisk z dziedziny fizyki jądrowej i fizyki cząstek elementarnych zmiany mas cząstek, spowodowane zmianami ich energii, są stosunkowo znaczne i całkowicie potwierdzają podaną zależność. Ciało o zerowej masie relatywistycznej (m = 0) nie posiada energii całkowitej (E = 0), po zsumowaniu poszczególnych przyrostów energii otrzymuje się E = mc2 . Wzór ten wyraża jedno z najważniejszych praw przyrody — zasadę równoważności masy i energii: Całkowita energia ciała jest równa iloczynowi jego masy relatywistycznej i kwadratu prędkości światła w próżni. W szczególności całkowita energia ciała spoczywającego w danym układzie odniesienia wynosi E₀ = m₀­­­­c². Jest to tzw. energia spoczynkowa. Można wykazać, że w przypadku układu ciał ich całkowita energia relatywistyczna nie ulega zmianie.

Wzór na energie kinetyczną: E_k = (m - m₀)c² E₂= m₀²c⁴+p²c²

WYPROWADZENIE WZORU: en. kinetyczna

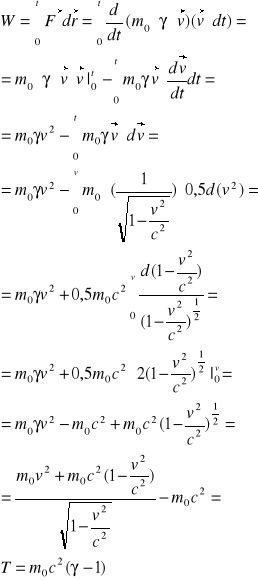
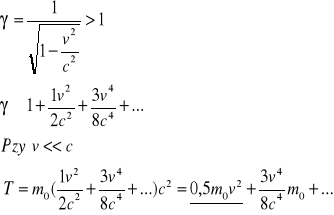
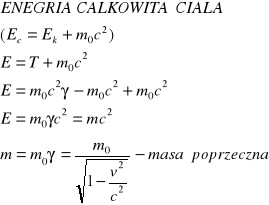
16. Defekt masy

Typowo relatywistyczne zjawiska:

Efekt Comptona, zjawisko Doplera, Kreacja i anihilacja par (czastek)* e ^- + e ⁺ =0 + 2hν powstają 2 kwanty promieniowania hν → e ^- + e ⁺ , Defekt masy (przy roztrzepaniu jąder uranu) - różnica między rzeczywistą masą jądra atomowego a jego liczbą masową. część masy przekształcona jest w energię oddziaływań wewnątrzjądrowych według wzoru E = mc Im większy jest defekt masy, im większa jest energia wiązania tym bardziej stabilnie jest powstałe jądro atomowe. Stabilne jądra mają w przybliżeniu taką samą liczbę neutronów i protonów.

m_0, m₀c rozpad → <- v₁ m_{0 1} -> v₂ m_{0 2}

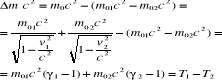
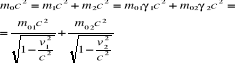
m₀>m₀₁ + m₀₂ ∆m = m₀-( m₀₁ + m₀₂ ) defekt masy
Energia wiązania jądra atomowego to różnica mas, tj. masa nukleonów tworzących jądro, wziętych każdy z osobna, i masy jądra, pomnożona przez c², gdzie c = 3 * 10⁸ m/s jest prędkością światła w próżni.

Według Einsteina, każdej masie m odpowiada energia określona wzorem: E = mc² Gdzie: m- masa, c - predkość światła = 300000 km/s Według tej równoważności każda zmiana energii musi być związana ze zmianą masy. Na przykład przy połączeniu atomów w molekuły masa maleje ze względu na oddaną energię wiązania. Z drugiej strony, chemiczna energia wiązania jest o wiele za mała, aby wywołać zauważalne zmiany masy.
Natomiast w zakresie jąder atomowych wyzwolona przez połączenie nukleonów energia wiązania jest równoważna zmianie masy rzędu 1 %. I dlatego może być określana przez porównanie masy jądra z masą nukleonów.
Należałoby oczekiwać, że masa jądra jest równa sumie mas zawartych w jądrze nukleonów. W rzeczywistości jest ona mniejsza i ten defekt masy /ubytek/ jest równoważny energii wiązania.

---