Doświadczenie 22
Celem doświadczenia jest wyznaczenie ciepła właściwego śrutu aluminiowego.
WPROWADZENIE
Ciepło jest formą energii przekazywanej od jednego ciała do drugiego. Przy zetknięciu się dwóch lub więcej ciał mających różne temperatury następuje między nimi przepływ ciepła. Ciepło przepływa od ciała mającego wyższą temperaturę do ciała mającego niższą temperaturę. Ciało oddające ciepło obniża swoją temperaturę, a ciało pobierające ciepło-podwyższa. Temperatura jest wielkością opisującą stan cieplny ciała.
Jednostką ciepła Q w układzie SI jest dżul [ J ]. Natomiast jednostką temperatury T jest jeden kelwin [ K ]. W życiu codziennym do określania temperatury t używamy innej jednostki - stopni Celsjusza [ ° C ]. Między oboma jednostkami zachodzi związek :
T= t+ 273,15
Przyrost temperatury w obu skalach jest więc jednakowy : ΔT= Δt
Ilość ciepła Q pobranego przy ogrzaniu ciała od temperatury T1 do T2 zależy od rodzaju ciała i jest proporcjonalny do jego masy m i uzyskanej zmiany temperatury. Tak samo jest w przypadku ciała oddającego ciepło i obniżającego swoją temperaturę od T2 do T1
Q = cmΔT ( 1 )
Współczynnik proporcjonalności c jest to średnie ciepło właściwe w zakresie temperatur od t1 do t2.
![]()
Ilość ciepła potrzebna do ogrzania jednostki masy ciała o jednostkę temperatury nazywamy ciepłem właściwym. Wzór definiujący je otrzymamy po przekształceniu wzoru ( 1 ).
![]()
Jednostką ciepła właściwego jest
![]()
WYZNACZANIE CIEPŁA WŁAŚCIWEGO CIAŁA STAŁEGO
Przy pomiarach ciepła właściwego posługujemy się kalorymetrem .
D M
A
B
N
Jest on skonstruowany tak, aby ciała znajdujące się w jego wnętrzu były odizolowane termicznie od otoczenia. Składa się on z naczynia wewnętrznego N, nazywanego kalorymetrem właściwym i naczynia zewnetrznego A, pełniącego rolę osłony aduabatycznej, czyli chroniącej kalorymetr właściwy przed wymianą ciepła z otoczeniem. Do pomiaru temperatury we wnętrzu kalorymetru służy termometr D. Natomiast mieszadełko M umożliwia przyspieszenie wyrównania temperatur wody i ciał wprowadzonych do kalorymetru. Naczynia są odizolowane od siebie za pomocą podstawek nie przewodzących ciepła.
Taka budowa kalorymetru umożliwia twierdzenie, że ilość ciepła oddana przez ciała cieplejsze równa jest ilości ciepła pobranego przez ciała zimniejsze. Twierdzenie to jest zgodne z zasadą zachowania energii. Pisząc równanie bilansu ciepła uwzględniamy też to ,że kalorymetr właściwy i mieszadełko także biorą udział w procesie wymiany ciepła.
Aby zmierzyć ciepło właściwe c ciała, ogrzewamy go do temperatury t1 i umieszczamy w kalorymetrze z wodą o temperaturze początkowej t0.Ustala się wspólna temperatura t wody,kalorymetru i badanego ciała. Ciało oddaje przy tym pewną ilość ciepła Q1 :
Q1 = m1c( t1 - t2 ) ( 2 )
Natomiast woda i kalorymetr pobierają ciepło Q2 :
Q2 = (mwcw +mkck )(t - t0) ( 3 )
mw - masa wody w kalorymetrze
mk - masa kalorymetru właściwego
cw - ciepło wody i kalorymetru
Zachodzi też równość :
Q1 = Q2 ( 4 )
gdyż cały układ ( ciało stałe, woda, kalorymetr ) jest izolowany cieplnie.
Ze wzorów 2 - 4 wynika :
![]()
( 5 )
![]()
Ilość ciepła potrzebna do ogrzania masy ciała o 1K nazywana jest pojemnością cieplną W. Jednostką pojemności cieplnej jest [ J/K ]. Jeśli do wzoru ( 5 ) wprowadzimy pojemność cieplną kalorymetru W = mkck , będzie on miał postać :
PRZEBIEG DOŚWIADCZENIA
Badane cialo ( śrut aluminiowy ) ważymy na wadze laboratoryjnej. Jego masę m1 wpisujemy do tabeli pomiarowej. Ważymy suchy kalorymetr właściwy z mieszadełkiem. Masa kalorymetru to mk . Do kalorymetru nalewamy obok 1/3 objętości zimnej wody.Całość ważymy - masa m2 , wg wzoru mw = m2 - m1 obliczamy masę wody.
Śrut wsypujemy do termostatu i ogrzewamy do temperatury 45°C. Ta temperatura w termostacie to t1. Mierzymy temperaturę wody w kalorymetrze i zapisujemy ją jako t0. Szybko wsypujemy śrut do kalorymetru. Mieszamy wodę w kalorymetrze i notujemy najwyższą temperaturę t jaka się ustali. Wyniki pomiaru wpisujemy do tabeli i obliczamy ciepło właściwe ciała ze wzoru ( 5 )
![]()
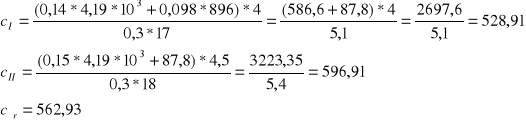
Następnie analogicznie przeprowadzamy drugi pomiar i obliczamy średnią wartość ciepła właściwego badanego ciała.
TABELA POMIAROWA
Nazwa badanego ciała : 300 g śrut |
Nr pomiaru |
I |
II |
|
Masa pustego kalorymetru z mieszadłem |
mk |
[ kg] |
0,098 g |
|
Ciepło właściwe kalorymetru |
ck |
[J/(kg*K)] |
896 |
|
Ciepło właściwe wody |
cw |
[J/(kg*K)] |
4,19*103 |
|
Masa kalorymetru z wodą |
m2 |
[kg] |
0,238 g |
0,254 g |
Masa wody w kalorymetrze |
mw |
[kg] |
0,140 g |
0,156 g |
Masa badanego ciała |
m1 |
[kg] |
0,3 g |
0,3 g |
Temp. początkowa wody i kalorymetru |
t0 |
[°C] |
24 |
23,5 |
Temperatura początkowa ciała |
t1 |
[°C] |
45,0 |
45,0 |
Temperatura końcowa układu |
t |
[°C] |
28 |
27 |
Ciepło właściwe badanego ciała |
ci |
[J/kg*K] |
528,94 |
596,91 |
Średnie ciepło właściwe badanego ciała |
c |
[J/kg*K] |
562,93 |
|
Wartość tablicowa ciepła właściwego |
ctab |
[J/kg*K] |
896 |
|
Bład bezwgl.wzgl.wartości tablicowej |
Δctab |
[J/kg*K] |
104,63 |
|
Bład względny wzgl.wartości tablicowej |
Δctab/ctab |
[%] |
0,12 |
|
RACHUNEK BŁĘDÓW
Błąd obliczamy tylko dla jednego z dwóch pomiarów. Do wzoru ( 5 ) wprowadzamy dla uproszczenia zapisów nowe oznaczenia :
tx ≡ t - t0 , a w ty ≡ t1 - t :
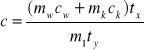
Zakładamy, że cw i ck nie są obarczane błędem.
Błąd względny Δc obliczamy na podstawie powyższego wzoru metodą różniczki zupełnej :
Δ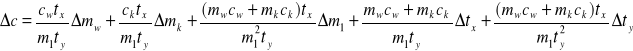
m - dokładnośc ważenia
Δm1 = Δmk = Δm
Δmw = 2Δm Δm = 0,001
Δt - dokładność odczytu temperatury Δt = 0,1
Δtx=Δty= 2Δt
Wzór na Δc można przekształcić do postaci łatwiejszej do obliczeń :
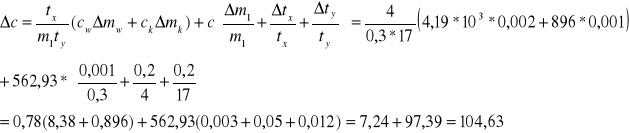
![]()
![]()
![]()
![]()
![]()
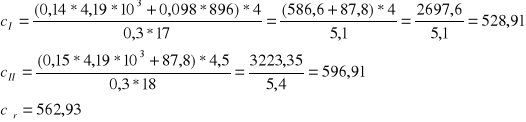
![]()
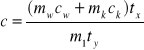
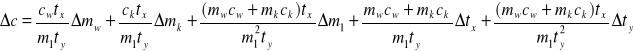

Wyszukiwarka
Podobne podstrony:
Ćwiczenie 24, Ćwiczenie 24, Karolina Wyrwas
Ćwiczenie 62, Ćwiczenie 62 (4), Karolina Wyrwas
Ćwiczenie64, Ćwiczenie 64 (1), Karolina Wyrwas
Ćwiczenie 24, Ćwiczenie 24 (3), Karolina Wyrwas
sprawozdania z fizyki, 22, Karolina Oleńska
sprawozdanie cwiczenie 22, studia, agrobiotechnologie
ćwiczenia i wykłady - 22 i 23 maja 2010r, Postępowanie cywilne
22. Kroki ustalania ceny, Materiały PSW Biała Podlaska, ZiPM- ćwiczenia
mechana, ruch-plaski-wahadlo3, Data wykonania ćwiczenia: 22
Cwiczenie 22 i
chemia fizyczna-ćwiczenie 22, chemia w nauce i gospodarce Uł, semestr V, sprawozdania chemia fizyczn
Ćwiczenie Chemia 2 (18 10 22 10 2010 r )
cwiczenie nr 1 2011 10 02 13 35 22
mechana, ruch-plaski-wahadlo, Data wykonania ćwiczenia: 22
45 Arkuszy ćwiczeniowych Matura angielski rozmowy sterowane, Arkusz ćwiczeniowy 22, Arkusz ćwiczenio
mechana, ruch-plaski-wahadlo, Data wykonania ćwiczenia: 22
45 Arkuszy ćwiczeniowych Matura angielski rozmowy sterowane, Arkusz ćwiczeniowy 22, Arkusz ćwiczenio
więcej podobnych podstron