POLITECHNIKA POZNAŃSKA INSTYTUT ELEKTROTECHNIKI PRZEMYSŁOWEJ Zakład Podstaw Elektrotechniki |
|||
Laboratorium Podstaw Elektrotechniki Ćwiczenie nr 13 Temat: Układy trójfazowe niesymetryczne |
|||
Rok akademicki: 2006/2007 Wydział Elektryczny Studia dzienne magisterskie Grupa: E5 |
Wykonawcy:
|
Data |
|
|
|
Wykonania ćwiczenia |
Oddania sprawozdania |
|
|
07.05.2007r
|
28.05.2007r |
|
|
Ocena: |
|
Uwagi:
|
|||
1. Wiadomości teoretyczne
(Rodzaje niesymetrii, obliczanie obwodów niesymetrycznych gwiazdowych, trój- i czteroprzewodowych, obliczanie obwodów niesymetrycznych trójkątnych, wykresy wektorowe).
2. Przebieg ćwiczenia
2.1. Pomiary prądów i napięć w układzie trójfazowym przy obciążeniu niesymetrycznym typu gwiazda z przewodem zerowym i bez
2.1.1. Schemat połączeń
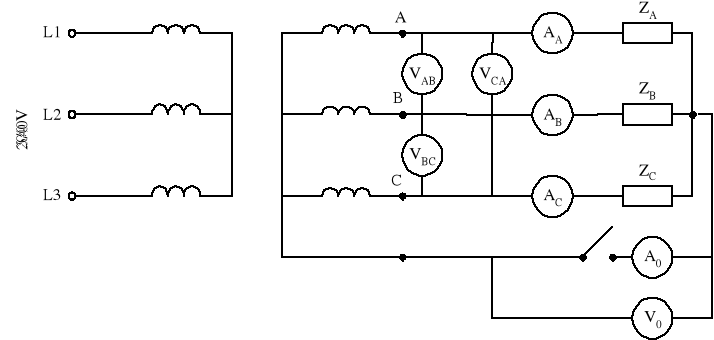
Dane: ZN = 0,33
2.1.2. Przebieg pomiarów
Zestawić układ przedstawiony w punkcie 2.1.1. Zmieniając układy połączyć zgodnie z tabelą przedstawioną w punkcie 2.1.3. odczytać wskazania wszystkich mierników. Wyniki pomiarów zamieścić w tabeli 2.1.3.
2.1.3. Tabela pomiarów
Lp |
Układ połączeń |
Przewód zerowy |
Wartość impedancji |
UAB |
UBC |
UCA |
EA |
EB |
EC |
IA |
IB |
IC |
IN |
UN |
||
|
|
|
ZA |
ZB |
ZC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[ၗ] |
[ၗ] |
[ၗ] |
[V] |
[V] |
[V] |
[V] |
[V] |
[V] |
[A] |
[A] |
[A] |
[A] |
[V] |
1. |
przerwa w fazie B |
tak |
-j159 |
Ⴅ |
220 |
74 |
73 |
73 |
42 |
42 |
42 |
0,28 |
0 |
0,2 |
0,15 |
- |
|
|
brak |
-j159 |
Ⴅ |
220 |
74 |
73 |
73 |
42 |
42 |
42 |
0,28 |
0 |
0,27 |
- |
52 |
2. |
zwarcie w fazie C |
brak |
-j159 |
220 |
0 |
73 |
73 |
73 |
42 |
42 |
42 |
0,47 |
0,3 |
0,25 |
- |
42 |
3. |
niesyme- tryczny |
brak |
-j159
|
220 |
220 |
72 |
72 |
72 |
42 |
42 |
42 |
0,34 |
0,33 |
0,1 |
- |
29 |
|
|
brak |
220
|
-j159 |
220 |
72 |
72 |
73 |
41 |
41 |
41 |
0,11 |
0,34 |
0,33 |
- |
29 |
|
|
brak |
220
|
220 |
-j159 |
73 |
73 |
73 |
42 |
42 |
42 |
0,33 |
0,11 |
0,34 |
- |
29 |
4. |
brak zasilania fazy „A” po stronie pierwotnej transfor-matora |
brak |
-j159 |
220 |
220 |
36 |
70 |
35 |
0 |
36 |
36 |
0,3 |
0,25 |
0,05 |
- |
2,58 |
2. 1. 4. Obliczenia analityczne
Wykonać obliczenia poszczególnych wielkości zawartych w tabeli w punkcie 2.1.4., w postaci Aexp(j), odnosząc je do napięcia EA, zakładając że układ napięć źródłowych jest układem symetrycznym(z wyjątkiem pkt. 4)
2. 1. 4. 1. Przerwa w fazie B (z przewodem zerowym)
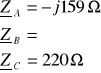
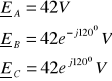
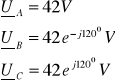
Przerwa w fazie B i obecność przewodu zerowego wymuszają warunki:
![]()
![]()
![]()
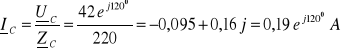
![]()
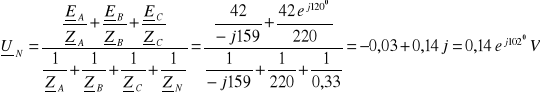
2. 1. 4. 1. Przerwa w fazie B (bez przewodu zerowego)
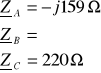
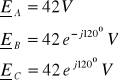
Przerwa w fazie B i brak przewodu zerowego wymuszają warunki:
![]()
![]()
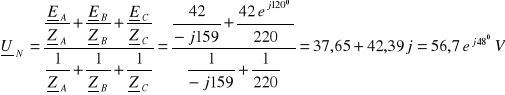
![]()
![]()
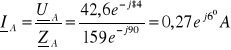
![]()
![]()
-21 - j36,37 -37,65 - j42,39 = -58,65 -j78,76 =98,19e - j127 V
2. 1. 4. 2. Zwarcie w fazie C
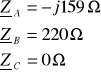
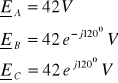
Zwarcie w fazie C i brak przewodu zerowego wymuszają warunki:
![]()
![]()
![]()
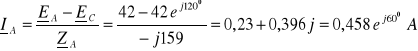
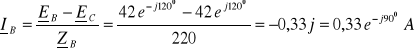
![]()
![]()
![]()
![]()
2. 1. 4. 3. niesymetryczny (bez przewodu zerowego)
a)
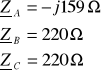
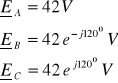
Brak przewodu zerowego wymusza warunek:
![]()
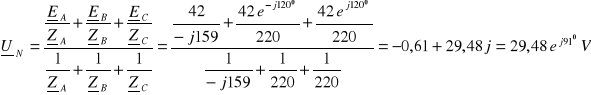
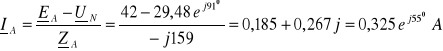
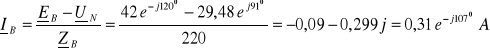
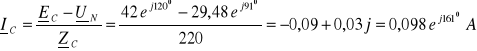
![]()
![]()
![]()
b)
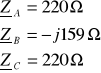
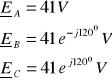
Brak przewodu zerowego wymusza warunek:
![]()
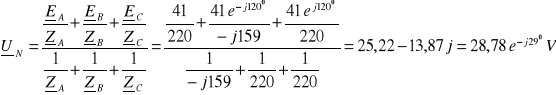
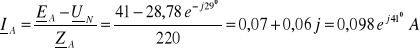
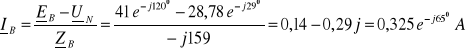
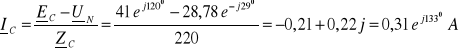
![]()
![]()
![]()
c)
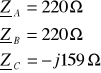
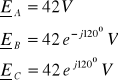
Brak przewodu zerowego wymusza warunek:
![]()
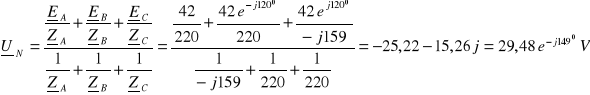
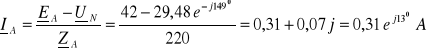
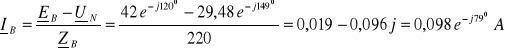
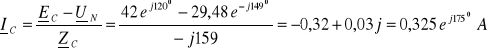
![]()
![]()
![]()
2. 1. 4. 4. Brak zasilania fazy „A” po stronie pierwotnej zasilania
Z twierdzenia cosinusów wyznaczamy kąty w odpowiadającym obwodzie niesymetrycznym trójkątnym:
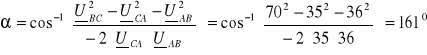
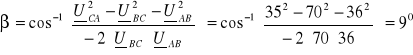
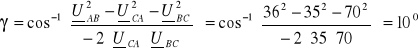
Po otrzymanych wynikach obliczeń analitycznych widać, że trójkąt napięć jest odkształcony.
Napięcie źródłowe EA jest naszym napięciem odniesienia, otrzymujemy więc następujący układ napięć międzyfazowych:
![]()
![]()
![]()
Napięcie źródłowe EA=0 stąd:
![]()
![]()
![]()
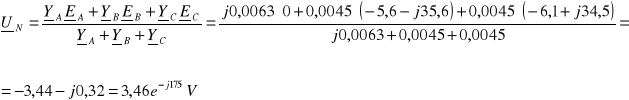
![]()
![]()
![]()
![]()
![]()
![]()
Tabela wyników obliczeń
L.p |
Układ połączeń |
Przewód zerowy |
UA |
UB |
UC |
UN |
IA |
IB |
IC |
IN |
|
|
|
[V] |
[V] |
[V] |
[V] |
[A] |
[A] |
[A] |
[A] |
1. |
przerwa w fazie B |
tak |
42 |
42e-j120 |
42ej120 |
- |
0,264ej90 |
0 |
0,19ej120 |
0,43ej102 |
|
|
brak |
42,6e-j84 |
98,19e-j127 |
58,96e-j174 |
56,7ej48 |
0,27ej6 |
0 |
0,27e-j174 |
- |
2. |
zwarcie w fazie C |
brak |
72,8e-j30 |
72,6e-j90 |
0 |
42ej120 |
0,458ej60 |
0,33e-j90 |
0,238e-j164 |
- |
3. |
niesymetryczny |
brak |
51,7e-j35 |
68,2e-j107 |
21,6ej161 |
29,48ej90 |
0,325ej55 |
0,31e-j108 |
0,098ej161 |
- |
|
|
brak |
21,6ej41 |
51,6e-j155 |
68,2ej33 |
28,78e-j29 |
0,098ej41 |
0,325e-j65 |
0,31ej133 |
- |
|
|
brak |
68,2ej13 |
21,6e-j79 |
51,6ej85 |
29,48e-j149 |
0,31ej13 |
0,098e-j79 |
0,325ej175 |
- |
4. |
brak zasilania fazy „A” po stronie pierwotnej transformatora |
brak |
3,46ej5 |
35e-j94 |
35ej94 |
3,46e-j175 |
0,02ej95 |
0,16e-j94 |
0,16ej94 |
- |
2.2. Pomiary prądów i napięć w układzie trójfazowym przy obciążeniu
niesymetrycznym typu trójkąt
2.2.1. Schemat połączeń
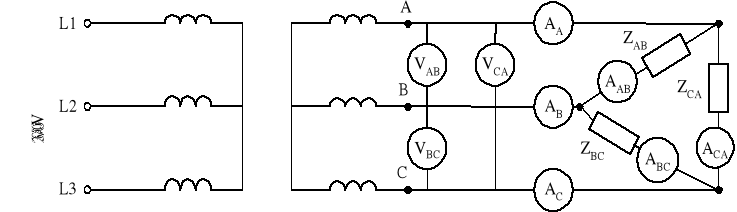
2.2.2. Przebieg pomiarów
Zestawić układ przedstawiony w punkcie 2.2.1. Zmieniając układy połączeń zgodnie z tabelą przedstawioną w punkcie 2.2.3 odczytać wskazania wszystkich mierników. Wyniki pomiarów zamieścić w tabeli 2.2.3.
2.2.3. Tabela pomiarów
Lp |
Układ połączeń |
ZAB |
ZBC |
ZCA |
UAB |
UBC |
UCA |
IA |
IB |
IC |
IAB |
IBC |
ICA |
|
|
[ၗ] |
[ၗ] |
[ၗ] |
[V] |
[V] |
[V] |
[A] |
[A] |
[A] |
[A] |
[A] |
[A] |
1. |
niesymetry- czny |
-j159 |
220 |
220 |
73 |
71 |
73 |
0,26 |
0,78 |
0,6 |
0,47 |
0,34 |
0,33 |
2. |
przerwa w fazie AB |
Ⴅ |
220 |
220 |
72 |
71 |
72 |
0,34 |
0,34 |
0,58 |
0 |
0,34 |
0,33 |
3. |
przerwa w fazie A po stronie wtórnej |
-j159 |
220 |
220 |
42 |
71 |
53 |
0 |
0,58 |
0,58 |
0,27 |
0,34 |
0,27 |
4. |
brak zasilania fazy „A” po stronie pierwotnej |
-j159 |
220 |
220 |
50 |
72 |
56 |
0,05 |
0,52 |
0,5 |
0,47 |
0,18 |
0,16 |
2.2.4. Obliczenia analityczne
Wykonać obliczenia poszczególnych wielkości zawartych w tabeli w punkcie 2.2.4., odnosząc je do napięcia UAB
2. 2. 4. 1. niesymetryczny
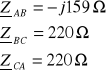
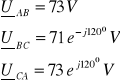
![]()
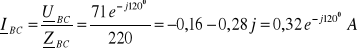
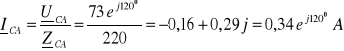
![]()
![]()
![]()
2. 2. 4. 2. Przerwa w fazie AB po stronie wtórnej
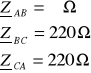
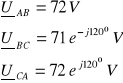
![]()
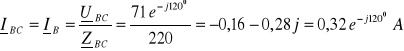
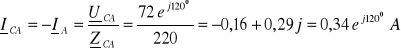
![]()
2. 2. 4. 3. Przerwa w fazie „A” po stronie wtórnej
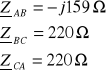
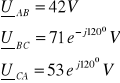
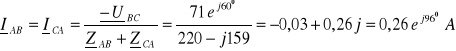
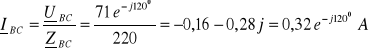
![]()
![]()
2. 2. 4. 4. Brak zasilania fazy „A” po stronie pierwotnej
Z twierdzenia cosinusów mamy:
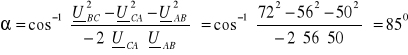
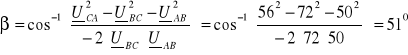
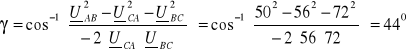
Stąd obliczamy napięcia międzyfazowe, a dalej prądy:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Tabela wyników obliczeń
Lp. |
Układ połączeń |
postać wyniku |
UAB |
UBC |
UCA |
IAB |
IBC |
ICA |
IA |
IB |
IC |
|
|
|
[V] |
[V] |
[V] |
[A] |
[A] |
[A] |
[A] |
[A] |
[A] |
1 |
niesyme- |
algebr. |
73 |
-35,5-j61,5 |
-36,5+j63 |
J0,46 |
-0,16-j0,28 |
-0,17+j0,29 |
-0,16-j0,18 |
0,16+j0,74 |
-j0,57 |
|
|
wykład. |
73 |
71e-j120 |
73ej120 |
0,46ej90 |
0,32e-j120 |
0,34ej120 |
0,24ej48 |
0,76e-j102 |
0,57ej90 |
2 |
przerwa w fazie AB |
algebr. |
72,1 |
-35,5-j61,5 |
-36,2+j62,6 |
0 |
-0,16-j0,28 |
-0,17+j0,29 |
0,17+j0,29 |
0,17-j0,29 |
-j0,57 |
|
|
wykład. |
72 |
71e-j120 |
72ej120 |
0 |
0,32e-j120 |
0,34ej120 |
0,33ej60 |
0,33e-j120 |
0,57ej90 |
3 |
przerwa w fazie A |
algebr. |
41,3 |
-35,5-j61,5 |
-26,5+j45,9 |
-0,03+j0,26 |
-0,16-j0,28 |
-0,03+j0,26 |
0 |
0,14+j0,54 |
-0,14-j0,54 |
|
|
wykład. |
42 |
71e-j120 |
53ej120 |
0,26ej96 |
0,32e-j120 |
0,26ej96 |
0 |
0,56ej76 |
0,56e-j104 |
4 |
brak zasilania fazy „A” |
algebr. |
52,7 |
-43-j57,5 |
-7,8+j55,5 |
j0,315 |
-0,19+j0,26 |
-0,03+j0,25 |
0,03-j0,07 |
-0,19-j0,59 |
0,15+j0,52 |
|
|
wykład. |
50 |
72e-j127 |
56ej98 |
0,315ej90 |
0,32e-j127 |
0,25ej98 |
0,074e-j62 |
0,62e-j108 |
0,54ej74 |
3. Wykresy wskazowe.
Wykres wektorowy prądów i napięć dla układu trójfazowego typu gwiazda-gwiazda, czteroprzewodowego. Przypadek: przerwa w fazie B:
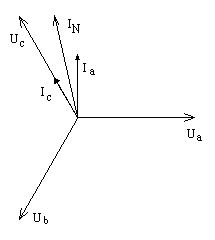
3.2. Wykres wektorowy prądów i napięć dla układu trójfazowego typu gwiazda-gwiazda.
Przypadek: zwarcie w fazie C:
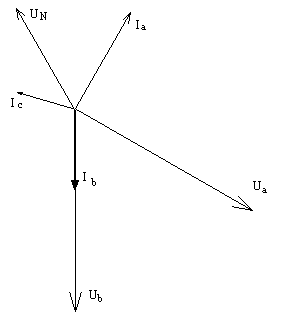
3.3. Wykres wektorowy prądów i napięć dla układu trójfazowego typu gwiazda-trójkąt.
Przypadek: niesymetryczny:
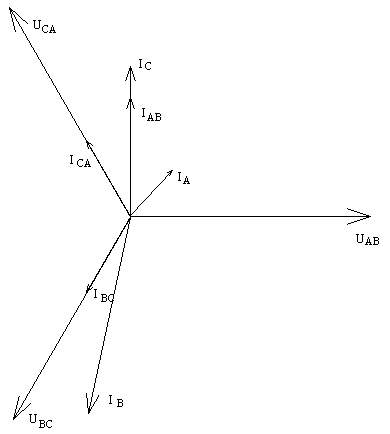
3.4. Wykres wektorowy prądów i napięć dla układu trójfazowego typu gwiazda-trójkąt.
Przypadek: przerwa w fazie AB:
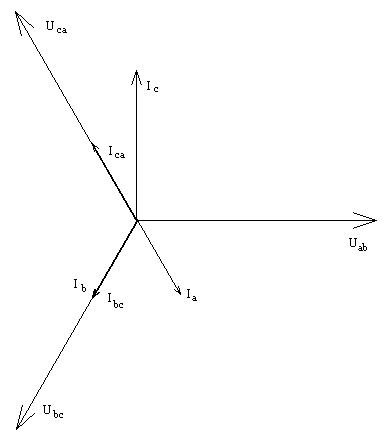
4. Wnioski i uwagi końcowe
Wyniki pomiarów i wynik obliczeń nie odbiegają znacznie od siebie, w niektórych przypadkach są identyczne. Niewielkie odchyłki mogą być spowodowane błędem wynikającym z klasy dokładności użytych przyrządów pomiarowych.
Różnica między obliczeniami, a pomiarami danych wielkości wynika z tego, że w obliczeniach podany zastał kąt przesunięcia, co w praktyce nie zostało zmierzone.
W połączeniu odbiornika w gwiazdę w pierwszym przypadku można zaobserwować wzrost napięcia na odbiornikach gdy nie ma podłączonego przewodu zerowego. Rosną również prądy w poszczególnych fazach odbiornika.
W przypadku braku zasilania fazy A po stronie pierwotnej transformatora, przy połączeniu odbiorników w trójkąt, zauważono, iż prądy fazowe są o wiele wyższe, co do wartości niż w przypadku połączenia odbiorników w trójkąt.
Wykresy wskazowe wykonałem na podstawie dokonanych obliczeń i sporządzone w programie wskaz.
Przełączanie gwiazda-trójkąt ma zastosowanie m. in. w sterowaniu silnikiem trójfazowym. W początkowej fazie rozruchu uzwojenia fazowe łączy się w gwiazdę. To powoduje, że prąd pobierany z sieci oraz moment obrotowy są ok. 1,73 (pierwiastek z 3) mniejsze niż w przypadku załączenia silnika do sieci przy połączeniu uzwojeń w trójkąt. Praca przy połączeniu w trójkąt jest oszczędniejsza, gdyż przy takiej samej pobieranej energii silnik wytwarza większe napięcie na uzwojeniach i większą moc na wale.
Innym zastosowaniem zamiany układu połączeń jest łączenie transformatorów. Układ połączeń gwiazda - gwiazda (Yy) jest stosowany w transformatorach wszystkich napięć i mocy znamionowych, przeznaczonych do pracy w układach o małej asymetrii obciążeń poszczególnych faz, dlatego właśnie układy Yy znajdują powszechne zastosowanie w transformatorach na napięcie wysokie i najwyższe, ze względu na występowanie w tych sieciach niewielkich asymetrii obciążeń. Układ Yy jest zdecydowanie najtańszy. Transformatory o górnym napięciu 110 kV i dolnym średnim, instalowane w stacjach elektroenergetycznych zasilających zakłady przemysłowe, mają na ogół układ połączeń uzwojeń gwiazda - trójkąt (Yd), co powoduje, że nie są wrażliwe na asymetrię obciążeń.
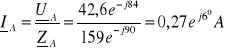
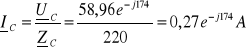
Wyszukiwarka
Podobne podstrony:
moje sprawko 4(1), Politechnika Poznańska ZiIP, III semestr, OCiS
OPP opracowane moje, ZiIP Politechnika Poznańska, Organizacja Przygotowania Produkcji
3-fazowka Miko, układy 3-faz. niesymetryczne 2, POLITECHNIKA POZNAŃSKA
3-fazowka Seb, 1Ukł 3faz niesymetryczne, POLITECHNIKA POZNAŃSKA
sprawko 5 moje oc, Politechnika Poznańska ZiIP, III semestr, OCiS
moje sprawozdanie, POLITECHNIKA POZNAŃSKA, LOGISTYKA, semestr I, mechanika i wytrzymałość materiałów
Układy trójfazowe niesymetryczne - j, Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Labor
MO - sprawozdanie 2(1), Politechnika Poznańska, Mechatronika, SEMESTR I, Odlewnictwo
egz TRB I 2009 c, Politechnika Poznańska, Budownictwo, Technologia Robót Budowlanych, Zaliczenie wyk
KONWENCJA BERNEŃSKA, MiBM Politechnika Poznanska, VII semestr TPM, Ochrona Własności Intelektualnej,
03 - Pomiar twardości sposobem Brinella, MiBM Politechnika Poznanska, IV semestr, labolatorium wydym
MW zaliczenie, Politechnika Poznańska ZiIP, IV semestr, IV semestr, Techniki pomiarowe, TechnikiPom,
c3 stal po ob ciep-chem, Politechnika Poznańska, Edukacja Techniczno Informatyczna, Semestr II, Mate
Pojęcia, MiBM Politechnika Poznanska, VII semestr TPM, Ochrona Własności Intelektualnej, wojtysiak,
zaliczenie odpowiedzi, Politechnika Poznańska - Wydział Budowy Maszyn i Zarządzania, Mechanika i Bud
Macierze i wyznaczniki, Politechnika Poznańska, Elektrotechnika, Matematyka, semestr 2
307 (2), Politechnika Poznańska (PP), Fizyka, Labolatoria, fiza sprawka, optyka
więcej podobnych podstron